1.1 基本计数原理 课件 22张PPT
文档属性
| 名称 | 1.1 基本计数原理 课件 22张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-05 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
计数(count) 亦称数数。算术的基本概念之一。指的是数事物个数的过程。计数时,通常是手指着每一个事物,一个一个地数,口里念着正整数列里的数1,2,3,4,5等,和所指的事物进行一一对应,这种过程称为计数。
百度百科:
问题:
引例:北京小汽车新车选车牌曾经有一种方法是网上自编号牌,原则是京N开头,后面一共有五位,后两位必须是数字,前三位其中有两个字母(去掉I,O)和一个数字,那么,按照这样的要求,可以组成多少种不同的车牌?
问题1: 咱班同学准备去南海子公园游玩,去公园之前,班长去学校的小卖部买一瓶水,小卖部货架的第一层放有8种不同品牌的矿泉水,第二层放有6种不同品牌的苏打水,那么他完成这件事一共有多少种不同的方法?
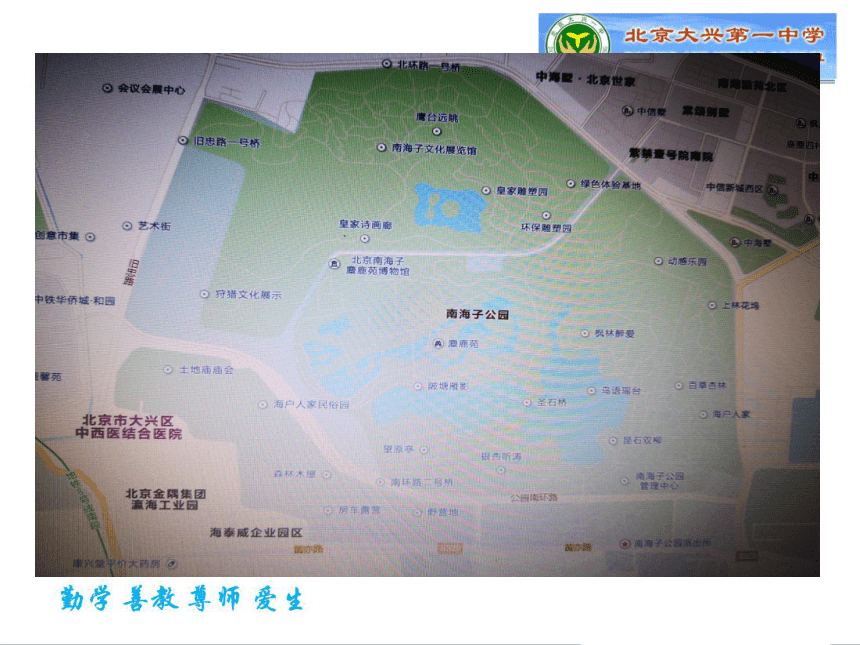
问题2 从大兴一中到南海子公园,我们搜索高德地图选择出行方式,
出租车有 3种方法(滴滴快车,神州专车,普通出租车),
公交出行有 2种方法(兴16,兴59),
骑行有 2种方法(自行车,电动车),
那么完成这件事一共有几种方法?
大巴车有1种方法
追问:小卖部货架的第一层放有8种不同品牌的矿泉水,第二层放有6种不同品牌的苏打水,第三层放有5种不同品牌的纯净水。。。。。
这两个计数问题有什么共同特点呢?
(1)完成一件事
(2)分类
(3)每类方案中的每一种方法都能独立 完成这件事情
(4)相加
分类加法计数原理:
一般地,如果完成一件事有类不同方案,在第1类方案中有 种不同的方法,在第2类方案中有 种不同的方法…,在第n类方案中有
种不同的方法,那么完成这件事共有 种不同方法
问题3 我们从北门进麋鹿苑,
主要景点有博物馆,观鸟台,麋鹿散养区等
回忆4月22日的游览路线
问题3 我们从北门进麋鹿苑,游览的顺序依次是博物馆,观鸟台,麋鹿散养区,最后到南海子公园的牡丹园,北门到博物馆有 3种方法,从博物馆到观鸟台有 2 种方法,从观鸟台到麋鹿散养区有4 种方法,从麋鹿散养区到牡丹园有 2 种方法,
(1)从北门经博物馆到观鸟台一共有多少种方法?
(2)从北门经博物馆和观鸟台到麋鹿散养区一共有多少种方法?
(3)从北门经博物馆、观鸟台、麋鹿散养区到牡丹园一共有多少种方法?
类比加法计数原理,归纳问题3的特点,我们可以得到什么结论?
(1)完成一件事
(2)分步
(3)每步中的任一种方法都不能独立的完成这件事,只有各个步骤都完成才算做完这件事情
(4)相乘
分类加法计数原理:
一般地,如果完成一件事有类不同方案,在第1类方案中有 种不同的方法,在第2类方案中有 种不同的方法…,在第n类方案中有
种不同的方法,那么完成这件事共有 种不同方法
分步乘法计数原理
一般地,如果完成一件事要 n个步骤,做第1步有 种不同的方法,做第2步有 种不同的方法…,做第 n步有 种不同的方法,那么完成这件事共有 种不同方法.
完成一件什么事
利用两个计数原理进行计数的思维步骤:
有些问题往往不是单纯的“分类”“分步”可以解决的,而要将“分类”“分步”结合起来运用.分类要不重不漏,综合应用分类加法计数原理和分步乘法计数原理。
解决问题:
引例:北京小汽车新车选车牌曾经有一种方法是网上自编号牌,原则是京N开头,后面一共有五位,后两位必须是数字,前三位其中有两个字母(去掉I,O)和一个数字,那么,按照这样的要求,可以组成多少种不同的车牌?
用来计算完成一件事的方法种数
分类、相加
分步、相乘
每类方案中的每一种方法都能独立完成这件事情
每步依次完成才算完成这件事情(每步中的每一种方法不能独立完成这件事)
类类独立,不重不漏
步步相依,缺一不可
分类加法计数原理
分步乘法计数原理
相同点
不同点
注意点
总结提升:
(1)知识:
(2)解题方法:
弄清楚完成什么样的一件事
分类?
分步?
分类和分步?
列举?
不重不漏
缺一不可
先分类还是先分步?
一一列举,找规律
(3)思想方法:
1、分类与整合思想
2、转化与化归思想
(1)分类对象确定,标准统一
(2)不重复,不遗漏
(1)复杂化为简单
(2)含糊化为明朗
(3)抽象化为直观
练习:
从0,1,2,3,4,5中选2个数字,
(1)组成无重复的两位数,一共有____种不同的方法.
(2)组成无重复的两位数,并且为偶数,一共有____种不同的方法.
25
13
思考:如果是三位数呢?
(3)组成个位数字大于十位数字的两位数,一共有____种不同的方法.
10
谢谢!
计数(count) 亦称数数。算术的基本概念之一。指的是数事物个数的过程。计数时,通常是手指着每一个事物,一个一个地数,口里念着正整数列里的数1,2,3,4,5等,和所指的事物进行一一对应,这种过程称为计数。
百度百科:
问题:
引例:北京小汽车新车选车牌曾经有一种方法是网上自编号牌,原则是京N开头,后面一共有五位,后两位必须是数字,前三位其中有两个字母(去掉I,O)和一个数字,那么,按照这样的要求,可以组成多少种不同的车牌?
问题1: 咱班同学准备去南海子公园游玩,去公园之前,班长去学校的小卖部买一瓶水,小卖部货架的第一层放有8种不同品牌的矿泉水,第二层放有6种不同品牌的苏打水,那么他完成这件事一共有多少种不同的方法?
问题2 从大兴一中到南海子公园,我们搜索高德地图选择出行方式,
出租车有 3种方法(滴滴快车,神州专车,普通出租车),
公交出行有 2种方法(兴16,兴59),
骑行有 2种方法(自行车,电动车),
那么完成这件事一共有几种方法?
大巴车有1种方法
追问:小卖部货架的第一层放有8种不同品牌的矿泉水,第二层放有6种不同品牌的苏打水,第三层放有5种不同品牌的纯净水。。。。。
这两个计数问题有什么共同特点呢?
(1)完成一件事
(2)分类
(3)每类方案中的每一种方法都能独立 完成这件事情
(4)相加
分类加法计数原理:
一般地,如果完成一件事有类不同方案,在第1类方案中有 种不同的方法,在第2类方案中有 种不同的方法…,在第n类方案中有
种不同的方法,那么完成这件事共有 种不同方法
问题3 我们从北门进麋鹿苑,
主要景点有博物馆,观鸟台,麋鹿散养区等
回忆4月22日的游览路线
问题3 我们从北门进麋鹿苑,游览的顺序依次是博物馆,观鸟台,麋鹿散养区,最后到南海子公园的牡丹园,北门到博物馆有 3种方法,从博物馆到观鸟台有 2 种方法,从观鸟台到麋鹿散养区有4 种方法,从麋鹿散养区到牡丹园有 2 种方法,
(1)从北门经博物馆到观鸟台一共有多少种方法?
(2)从北门经博物馆和观鸟台到麋鹿散养区一共有多少种方法?
(3)从北门经博物馆、观鸟台、麋鹿散养区到牡丹园一共有多少种方法?
类比加法计数原理,归纳问题3的特点,我们可以得到什么结论?
(1)完成一件事
(2)分步
(3)每步中的任一种方法都不能独立的完成这件事,只有各个步骤都完成才算做完这件事情
(4)相乘
分类加法计数原理:
一般地,如果完成一件事有类不同方案,在第1类方案中有 种不同的方法,在第2类方案中有 种不同的方法…,在第n类方案中有
种不同的方法,那么完成这件事共有 种不同方法
分步乘法计数原理
一般地,如果完成一件事要 n个步骤,做第1步有 种不同的方法,做第2步有 种不同的方法…,做第 n步有 种不同的方法,那么完成这件事共有 种不同方法.
完成一件什么事
利用两个计数原理进行计数的思维步骤:
有些问题往往不是单纯的“分类”“分步”可以解决的,而要将“分类”“分步”结合起来运用.分类要不重不漏,综合应用分类加法计数原理和分步乘法计数原理。
解决问题:
引例:北京小汽车新车选车牌曾经有一种方法是网上自编号牌,原则是京N开头,后面一共有五位,后两位必须是数字,前三位其中有两个字母(去掉I,O)和一个数字,那么,按照这样的要求,可以组成多少种不同的车牌?
用来计算完成一件事的方法种数
分类、相加
分步、相乘
每类方案中的每一种方法都能独立完成这件事情
每步依次完成才算完成这件事情(每步中的每一种方法不能独立完成这件事)
类类独立,不重不漏
步步相依,缺一不可
分类加法计数原理
分步乘法计数原理
相同点
不同点
注意点
总结提升:
(1)知识:
(2)解题方法:
弄清楚完成什么样的一件事
分类?
分步?
分类和分步?
列举?
不重不漏
缺一不可
先分类还是先分步?
一一列举,找规律
(3)思想方法:
1、分类与整合思想
2、转化与化归思想
(1)分类对象确定,标准统一
(2)不重复,不遗漏
(1)复杂化为简单
(2)含糊化为明朗
(3)抽象化为直观
练习:
从0,1,2,3,4,5中选2个数字,
(1)组成无重复的两位数,一共有____种不同的方法.
(2)组成无重复的两位数,并且为偶数,一共有____种不同的方法.
25
13
思考:如果是三位数呢?
(3)组成个位数字大于十位数字的两位数,一共有____种不同的方法.
10
谢谢!
