1.1 基本计数原理 课件 23张PPT
文档属性
| 名称 | 1.1 基本计数原理 课件 23张PPT |
|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-05 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
思考:3名同学从5家农户里各选一家入住(可以选同一家),一共有多少种不同的入住方式?
计数问题:计算完成一件事的方法数的问题
1
2
3
4
5
问题1: 重庆的王先生想到西昌现场观看嫦娥一号卫星的发射,从重庆到西昌可以乘坐火车或者汽车,一天中,火车有3班,汽车有2班,问从重庆到西昌共有多少种不同的走法?
问题1: 重庆的王先生想到西昌现场观看嫦娥一号卫星的发射,从重庆到西昌可以乘坐火车或者汽车,一天中,火车有3班,汽车有2班,问从重庆到西昌共有多少种不同的走法.
分析: 从重庆到西昌有2类方法,
Ⅰ.乘火车,3种方法;
Ⅱ.乘汽车,2种方法;
所以 从重庆到西昌共有 3 + 2 = 5 种不同方法。
如果重庆到西昌,除了3班火车2班汽车外还有2班飞机,那么王先生有多少种不同的走法呢?
如果完成一件事情有n类不同的办法,在每一类中都有若干种不同方法,那么应当如何计数呢?
[探究]:
[延伸]:
共有: 3+2+2=7 种
分类加法计数原理
种不同的方法.
注意:每类方法都能独立完成这件事,不重复,不遗漏
例1:用前6个大写英文字母或1—9九个阿拉伯数字,给教室里的座位编号,总共能编出多少个不同的号码?
答:6+9=15
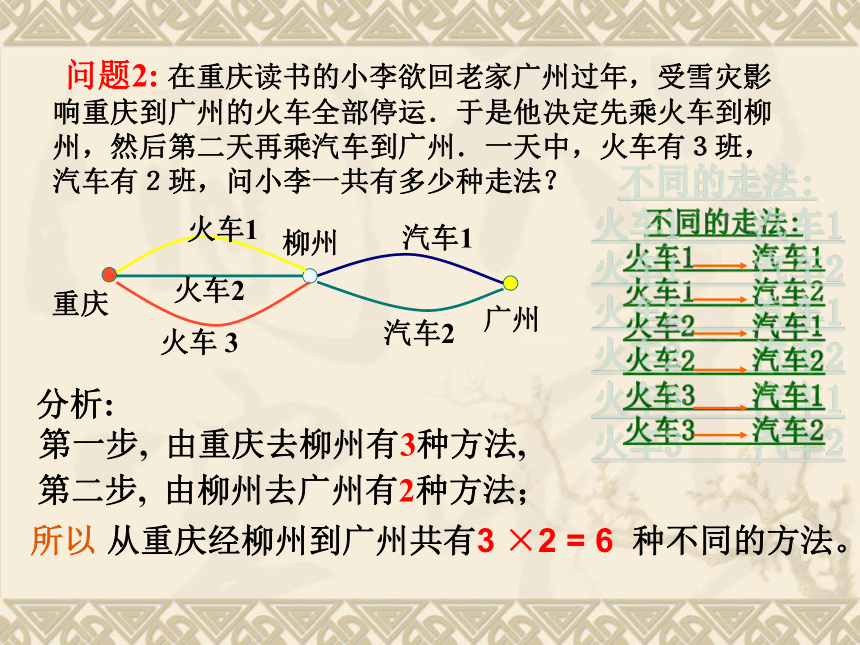
问题2: 在重庆工作的小李欲回广州老家过年,受雪灾影响重庆到广州的火车全部停运.于是他决定先乘火车到柳州,然后第二天再乘汽车到广州.一天中,火车有3班,汽车有2班,问小李一共有多少种走法?
问题2: 在重庆读书的小李欲回老家广州过年,受雪灾影响重庆到广州的火车全部停运.于是他决定先乘火车到柳州,然后第二天再乘汽车到广州.一天中,火车有3班,汽车有2班,问小李一共有多少种走法?
第二步, 由柳州去广州有2种方法;
分析:
第一步, 由重庆去柳州有3种方法,
所以 从重庆经柳州到广州共有3 ×2 = 6 种不同的方法。
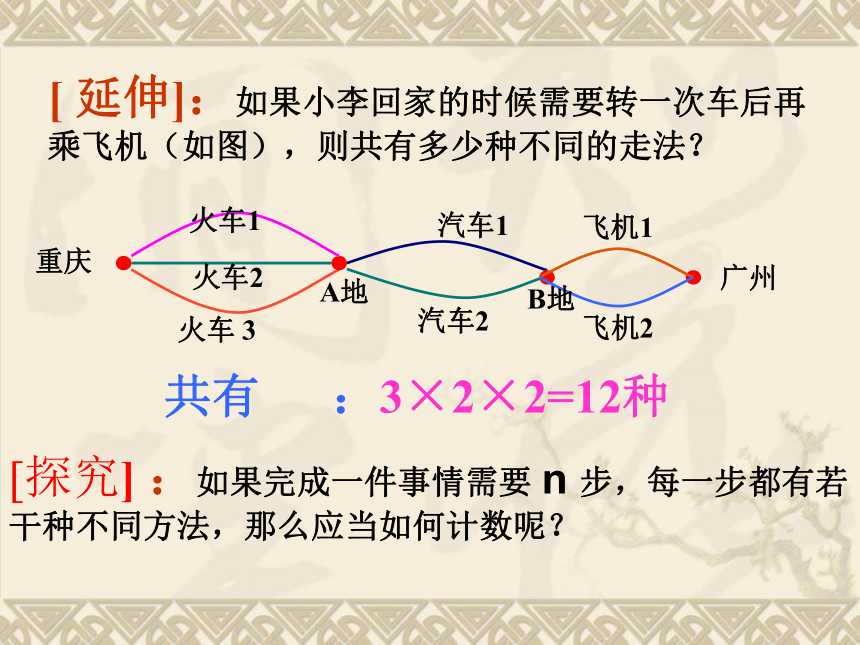
[探究] :如果完成一件事情需要 n 步,每一步都有若干种不同方法,那么应当如何计数呢?
[ 延伸]:如果小李回家的时候需要转一次车后再乘飞机(如图),则共有多少种不同的走法?
共有 :3×2×2=12种
分步乘法计数原理
种不同的方法.
注意只有每步都完成,事情才能完成.
用前六个大写英文字母中的一个和1~9九个阿拉伯数字中的一个,组成形如A1,B2的方式给卫星编号,总共能编出多少个不同的号码?
A1
A2
A3
A4
A5
A6
A7
A8
A9
9种
9种
所以,共有9+9+9+9+9+9=9×6=54种不同号码
例2
9种
…
…
完成一件事,共有n类方案,关键词“分类”
区别1
完成一件事,共分n个步骤,关键词 “分步”
区别2
区别3
每类方案的任何一个方法都能独立地完成这件事情
任何一步都不能独立完成这件事,只有各个步骤都完成了,才能完成这件事
相加
相乘
分类加法计数原理 分步乘法计数原理
例3:书架的第1层放有4本不同的语文书,第2层放有3本不同的数学书,第3层放有2本不同的英语书;
(1) 从书架上任取一本书,有多少种取法?
(2)从书架的第1、2、3层各取1本书,有多少种不同的取法?
4+3+2=9
4×3×2=24
(3)从书架上取两本不同学科的书,有多少种不同的取法
4×3+4×2+3×2=26
思考:3名同学从5家农户里各选一家入住(可以选同一家),一共有多少种不同的入住方式?
1
2
3
4
5
例4
练习1:第29届奥运会在中国北京举行,在乒乓球比赛中,中国队的马琳、王皓、王励勤包揽了男子单打的前三名。有4位女粉丝前去献花,请问可能出现多少种献花情况。
3×3×3×3 =34 = 81
练习2: 乘积展开后共有多少项?
3×3×5=45
①
⑤
②
③
④
练习3: 用红、黄、蓝3种颜色给下图中① ② ③ ④ ⑤五个区域涂色,要求相邻两个区域的颜色不同,有多少种不同的涂法?
解:涂色可分5步进行:
第一步:涂区域①,有3种选择;
第二步:涂区域② ,有2种选择;
第三步:涂区域③ ,有1种选择;
第四步:涂区域④ ,有1种选择;
第五步:涂区域⑤ ,有2种选择;
由分步计数原理得,涂法数为 3 × 2 × 1× 1× 2 = 12
如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路可以走,从丙地到丁地有2条路。从甲地到丁地共有多少种不同地走法?
解:如图所示,从总体上看,由甲到丁有两类不同的走法,
第一类,由甲经乙去丁,又需分两步,所以m1= 2×3 =6种不同的走法;
第二类,由甲经丙去丁,也需分两步,所以m2= 4×2 =8种不同的走法;
所以从甲地到丁地共有N=6 + 8 = 14种不同的走法。
练习4
3. 四名研究生各从A、B、 C三位教授中选一位作自己的导师,共有______种选法;三名教授从四名研究生中各选一位作自己的学生,共有_____种选法。
.
24
1.从 5 名同学中选出正、副组长各 1 名,有多少种不同的选法?
5×4=20
34
变式训练
2. 汉字在计算机的机器语言中是用16位的数字表示(0或1)
你如何数出16位数字共能表示多少个不同的汉字?
延伸阅读 常用汉字数量大约是2500到7000之间,根据统计:毛泽东所有的著作仅含3136个不同的汉字.
归
纳
推
理
分
类
讨
论
数学
源于生活
数学
用于生活
小结
分类计数原理与
分步计数原理
分类计数原理:针对的是“分类”问题,其各种方法互相独立,用其中任何一种方法都可以做完这件事。
分步计数原理:针对的是“分步”问题,各个步骤的方法相互依存,只有各个步骤都完成了才算做完这件事。
都是有关做一件事情的不同方法的种数的问题。
作业布置
1. 完成课本P12 A组1、2、3
2. 阅读课本P11:子集的个数有多少
明计数之道——反思过程 顺化原理
3. 成才之路课后强化1,2,4,6,8,10
1. 一件工作可以用两种方法完成。有5人会用第一种方法完成,另有4人会用第二种方法完成。选出一个人来完成这件工作,共有多少种选法?
2.乘积( a1+ a 2+ a 3 )( b1 + b 2 )(c1 + c2 + c3 + c4 + c5 )展开后共有项?
4 + 5 = 9
3×2×5=30
3、把四封不同的信任意投入三个信箱中,不同投法种数是( ) A. 12 B.64 C.81 D.7
4、火车上有10名乘客,沿途有5个车站,乘客下车的可能方式有 ( )种
A. 510 B. 105 C. 50 D. 以上都不对
C
A
课后思考
两大原理妙无穷
解题应用各不同
多思慎密最重要
茫茫数理此中求
思考:3名同学从5家农户里各选一家入住(可以选同一家),一共有多少种不同的入住方式?
计数问题:计算完成一件事的方法数的问题
1
2
3
4
5
问题1: 重庆的王先生想到西昌现场观看嫦娥一号卫星的发射,从重庆到西昌可以乘坐火车或者汽车,一天中,火车有3班,汽车有2班,问从重庆到西昌共有多少种不同的走法?
问题1: 重庆的王先生想到西昌现场观看嫦娥一号卫星的发射,从重庆到西昌可以乘坐火车或者汽车,一天中,火车有3班,汽车有2班,问从重庆到西昌共有多少种不同的走法.
分析: 从重庆到西昌有2类方法,
Ⅰ.乘火车,3种方法;
Ⅱ.乘汽车,2种方法;
所以 从重庆到西昌共有 3 + 2 = 5 种不同方法。
如果重庆到西昌,除了3班火车2班汽车外还有2班飞机,那么王先生有多少种不同的走法呢?
如果完成一件事情有n类不同的办法,在每一类中都有若干种不同方法,那么应当如何计数呢?
[探究]:
[延伸]:
共有: 3+2+2=7 种
分类加法计数原理
种不同的方法.
注意:每类方法都能独立完成这件事,不重复,不遗漏
例1:用前6个大写英文字母或1—9九个阿拉伯数字,给教室里的座位编号,总共能编出多少个不同的号码?
答:6+9=15
问题2: 在重庆工作的小李欲回广州老家过年,受雪灾影响重庆到广州的火车全部停运.于是他决定先乘火车到柳州,然后第二天再乘汽车到广州.一天中,火车有3班,汽车有2班,问小李一共有多少种走法?
问题2: 在重庆读书的小李欲回老家广州过年,受雪灾影响重庆到广州的火车全部停运.于是他决定先乘火车到柳州,然后第二天再乘汽车到广州.一天中,火车有3班,汽车有2班,问小李一共有多少种走法?
第二步, 由柳州去广州有2种方法;
分析:
第一步, 由重庆去柳州有3种方法,
所以 从重庆经柳州到广州共有3 ×2 = 6 种不同的方法。
[探究] :如果完成一件事情需要 n 步,每一步都有若干种不同方法,那么应当如何计数呢?
[ 延伸]:如果小李回家的时候需要转一次车后再乘飞机(如图),则共有多少种不同的走法?
共有 :3×2×2=12种
分步乘法计数原理
种不同的方法.
注意只有每步都完成,事情才能完成.
用前六个大写英文字母中的一个和1~9九个阿拉伯数字中的一个,组成形如A1,B2的方式给卫星编号,总共能编出多少个不同的号码?
A1
A2
A3
A4
A5
A6
A7
A8
A9
9种
9种
所以,共有9+9+9+9+9+9=9×6=54种不同号码
例2
9种
…
…
完成一件事,共有n类方案,关键词“分类”
区别1
完成一件事,共分n个步骤,关键词 “分步”
区别2
区别3
每类方案的任何一个方法都能独立地完成这件事情
任何一步都不能独立完成这件事,只有各个步骤都完成了,才能完成这件事
相加
相乘
分类加法计数原理 分步乘法计数原理
例3:书架的第1层放有4本不同的语文书,第2层放有3本不同的数学书,第3层放有2本不同的英语书;
(1) 从书架上任取一本书,有多少种取法?
(2)从书架的第1、2、3层各取1本书,有多少种不同的取法?
4+3+2=9
4×3×2=24
(3)从书架上取两本不同学科的书,有多少种不同的取法
4×3+4×2+3×2=26
思考:3名同学从5家农户里各选一家入住(可以选同一家),一共有多少种不同的入住方式?
1
2
3
4
5
例4
练习1:第29届奥运会在中国北京举行,在乒乓球比赛中,中国队的马琳、王皓、王励勤包揽了男子单打的前三名。有4位女粉丝前去献花,请问可能出现多少种献花情况。
3×3×3×3 =34 = 81
练习2: 乘积展开后共有多少项?
3×3×5=45
①
⑤
②
③
④
练习3: 用红、黄、蓝3种颜色给下图中① ② ③ ④ ⑤五个区域涂色,要求相邻两个区域的颜色不同,有多少种不同的涂法?
解:涂色可分5步进行:
第一步:涂区域①,有3种选择;
第二步:涂区域② ,有2种选择;
第三步:涂区域③ ,有1种选择;
第四步:涂区域④ ,有1种选择;
第五步:涂区域⑤ ,有2种选择;
由分步计数原理得,涂法数为 3 × 2 × 1× 1× 2 = 12
如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路可以走,从丙地到丁地有2条路。从甲地到丁地共有多少种不同地走法?
解:如图所示,从总体上看,由甲到丁有两类不同的走法,
第一类,由甲经乙去丁,又需分两步,所以m1= 2×3 =6种不同的走法;
第二类,由甲经丙去丁,也需分两步,所以m2= 4×2 =8种不同的走法;
所以从甲地到丁地共有N=6 + 8 = 14种不同的走法。
练习4
3. 四名研究生各从A、B、 C三位教授中选一位作自己的导师,共有______种选法;三名教授从四名研究生中各选一位作自己的学生,共有_____种选法。
.
24
1.从 5 名同学中选出正、副组长各 1 名,有多少种不同的选法?
5×4=20
34
变式训练
2. 汉字在计算机的机器语言中是用16位的数字表示(0或1)
你如何数出16位数字共能表示多少个不同的汉字?
延伸阅读 常用汉字数量大约是2500到7000之间,根据统计:毛泽东所有的著作仅含3136个不同的汉字.
归
纳
推
理
分
类
讨
论
数学
源于生活
数学
用于生活
小结
分类计数原理与
分步计数原理
分类计数原理:针对的是“分类”问题,其各种方法互相独立,用其中任何一种方法都可以做完这件事。
分步计数原理:针对的是“分步”问题,各个步骤的方法相互依存,只有各个步骤都完成了才算做完这件事。
都是有关做一件事情的不同方法的种数的问题。
作业布置
1. 完成课本P12 A组1、2、3
2. 阅读课本P11:子集的个数有多少
明计数之道——反思过程 顺化原理
3. 成才之路课后强化1,2,4,6,8,10
1. 一件工作可以用两种方法完成。有5人会用第一种方法完成,另有4人会用第二种方法完成。选出一个人来完成这件工作,共有多少种选法?
2.乘积( a1+ a 2+ a 3 )( b1 + b 2 )(c1 + c2 + c3 + c4 + c5 )展开后共有项?
4 + 5 = 9
3×2×5=30
3、把四封不同的信任意投入三个信箱中,不同投法种数是( ) A. 12 B.64 C.81 D.7
4、火车上有10名乘客,沿途有5个车站,乘客下车的可能方式有 ( )种
A. 510 B. 105 C. 50 D. 以上都不对
C
A
课后思考
两大原理妙无穷
解题应用各不同
多思慎密最重要
茫茫数理此中求
