1.3.1 二项式定理 课件 19张PPT
文档属性
| 名称 | 1.3.1 二项式定理 课件 19张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-05 21:43:52 | ||
图片预览






文档简介
(共19张PPT)
河南省偃师高中 任利梅
问题1:
问题2:
它研究的就是 (a+b)n 的展开式.
今天是星期三,再过8天之后是星期几?
如何利用两个计数原理得到 的展开式?
探究
在初中,我们用多项式乘法法则得到了 的展开式:
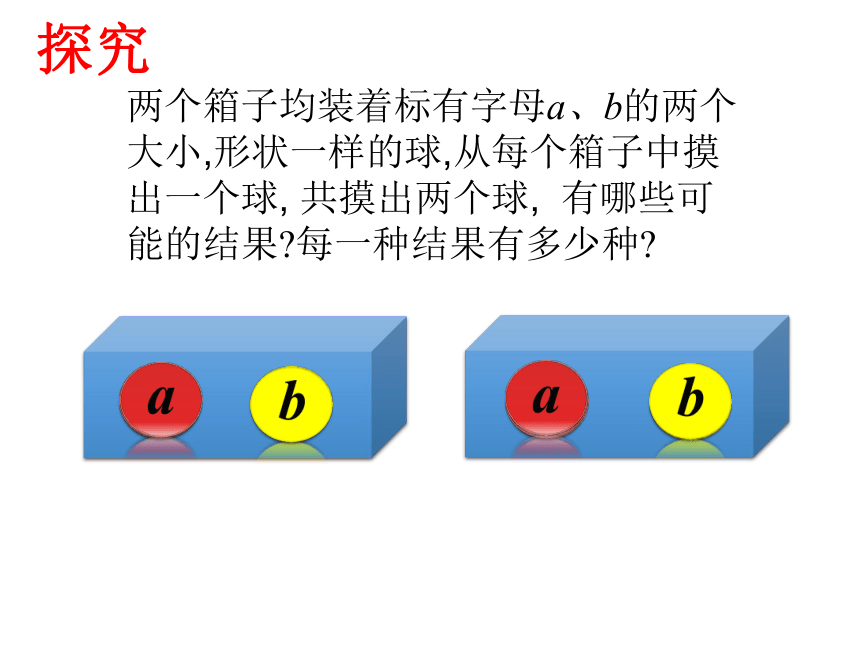
两个箱子均装着标有字母a、b的两个
大小,形状一样的球,从每个箱子中摸
出一个球, 共摸出两个球, 有哪些可
能的结果?每一种结果有多少种?
探究
从上述对具体问题的分析得到启发
an-k
二项式定理
二项式定理
一般地,
该公式称为二项式定理。其右端的多项式叫做(a+b)n的
二项展开式,共有n+1项。其中
3)若取a=1,b=x则得一个重要公式:
二项式定理
二项式定理
解:
若取a=1,b=x则得一个重要公式:
二项式定理
解:
例2.求 的二项展开式.
二项式定理
解:
例2.求 的二项展开式.
先化简,再展开。
解:
先化简,再展开。
二项式定理
解:
所以展开式第4项的系数是280,第4项的二项式系数是35.
二项式定理
解:
二项式定理
练习:P31 1、2、3、4
回顾反思 归纳总结
请同学们回顾整个过程,你在知识上和思想方法上都有哪些收获:
(1)二项式定理
(2)通项
(3)二项式系数与项的系数的区别
(4)思想方法
①归纳、猜想、证明的数学方法;
②用计数原理分析二项式的展开过程.
教学过程
课后作业
1.课本36页 习题1.3 A组第1~5题,B组第1题.
2.课时作业37页.
谢谢!
河南省偃师高中 任利梅
问题1:
问题2:
它研究的就是 (a+b)n 的展开式.
今天是星期三,再过8天之后是星期几?
如何利用两个计数原理得到 的展开式?
探究
在初中,我们用多项式乘法法则得到了 的展开式:
两个箱子均装着标有字母a、b的两个
大小,形状一样的球,从每个箱子中摸
出一个球, 共摸出两个球, 有哪些可
能的结果?每一种结果有多少种?
探究
从上述对具体问题的分析得到启发
an-k
二项式定理
二项式定理
一般地,
该公式称为二项式定理。其右端的多项式叫做(a+b)n的
二项展开式,共有n+1项。其中
3)若取a=1,b=x则得一个重要公式:
二项式定理
二项式定理
解:
若取a=1,b=x则得一个重要公式:
二项式定理
解:
例2.求 的二项展开式.
二项式定理
解:
例2.求 的二项展开式.
先化简,再展开。
解:
先化简,再展开。
二项式定理
解:
所以展开式第4项的系数是280,第4项的二项式系数是35.
二项式定理
解:
二项式定理
练习:P31 1、2、3、4
回顾反思 归纳总结
请同学们回顾整个过程,你在知识上和思想方法上都有哪些收获:
(1)二项式定理
(2)通项
(3)二项式系数与项的系数的区别
(4)思想方法
①归纳、猜想、证明的数学方法;
②用计数原理分析二项式的展开过程.
教学过程
课后作业
1.课本36页 习题1.3 A组第1~5题,B组第1题.
2.课时作业37页.
谢谢!
