1.3.1 利用导数判断函数的单调性 课件 18张PPT
文档属性
| 名称 | 1.3.1 利用导数判断函数的单调性 课件 18张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-07 09:42:33 | ||
图片预览





文档简介
(共18张PPT)
青海油田第一中学
授课内容:函数的单调性与导数
4、对数函数的导数:
5、指数函数的导数:
3、三角函数 :
1、常函数:(C)′? (c为常数);
2、幂函数 : (xn)′?
课 前 热 身
6、求下列函数的导数:
0
nxn?1
高二数学选修2-2第一章- -导数及其应用之
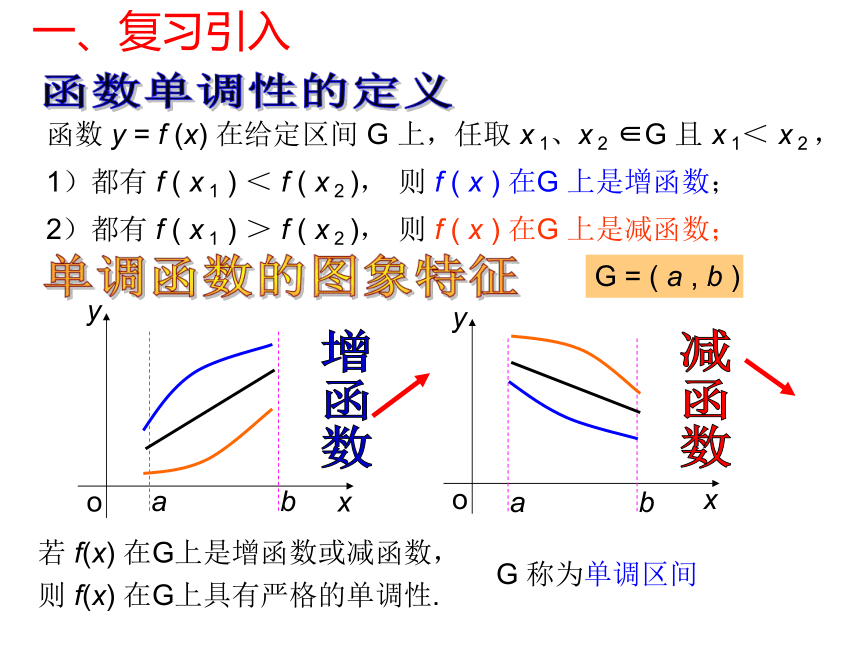
函数 y = f (x) 在给定区间 G 上,任取 x 1、x 2 ∈G 且 x 1< x 2 ,
1)都有 f ( x 1 ) < f ( x 2 ),
则 f ( x ) 在G 上是增函数;
2)都有 f ( x 1 ) > f ( x 2 ),
则 f ( x ) 在G 上是减函数;
若 f(x) 在G上是增函数或减函数,
则 f(x) 在G上具有严格的单调性.
G 称为单调区间
G = ( a , b )
一、复习引入
判断函数单调性有哪些方法?
图象法
减
增
如图:
思考:那么如何求出下列函数的单调性呢?
(1)f(x)=2x3-6x2+7 (2)f(x)=ex-x+1 (3)f(x)=sinx-x
发现问题:用单调性定义讨论函数单调性虽然
可行,但十分麻烦,尤其是在不知道函数图象
时。例如:2x3-6x2+7,是否有更为简捷的方法
呢?下面我们通过函数图象与导函数的正负来考察单调性与导数有什么关系。
x
y
O
x
y
O
x
y
O
x
y
O
y = x
y = x2
y = x3
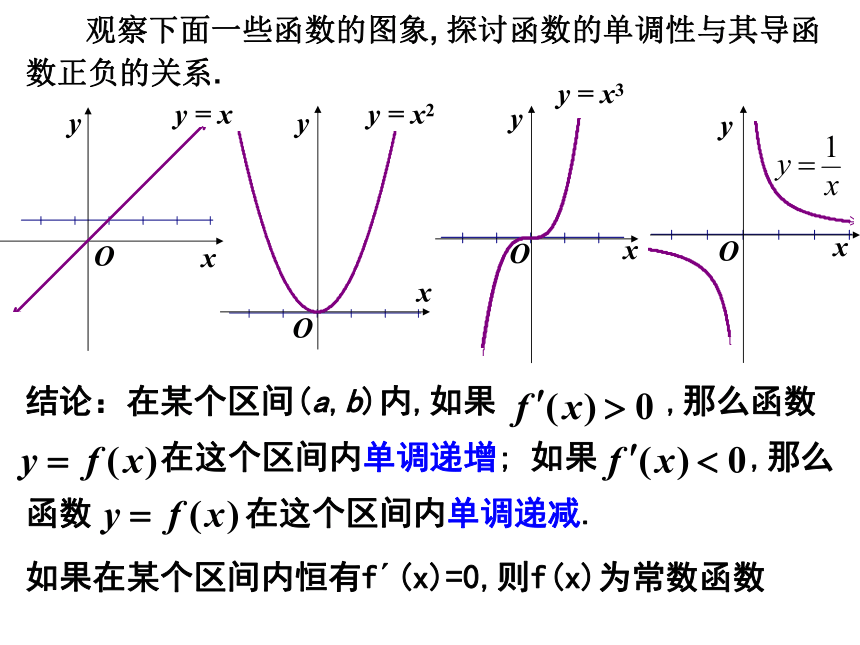
观察下面一些函数的图象, 探讨函数的单调性与其导函数正负的关系.
如果在某个区间内恒有f?(x)=0,则f(x)为常数函数
如果恒有f′(x)>0,
则 y=f(x)在这个区间(a,b)内单调递增;
如果恒有 f′(x)<0,
则y=f(x)在这个区间(a,b)内单调递减。
注意:应正确理解 “ 某个区间 ” 的含义,它必是定义域内的某个区间。
例1、已知导函数 的下列信息:
当10;
当x>4,或x<1时, <0;
当x=4,或x=1时, =0.试画出函数f(x)图象
的大致形状。
临界点
临界点
三、导数的应用:
C
变式
求函数 的单调区间。
理解训练:
注意:单调区间不可以并起来.
利用导数求函数单调区间的步骤:
说明:函数的单调区间一定是它的定义域的子区间,故求函数的单调区间一定首先要确定函数的定义域,在求出使导数的值为正或负的x的范围时,要与定义域求两者的交集.
变式、判断下列函数的单调性,并求出
单调区间:
(1) f(x)=x3+3x ;
从而函数f(x)=x3+3x
在x∈R上单调递增,
见右图。
(2) f(x)=sinx-x ; x∈(0,p)
从而函数f(x)=sinx-x
在x∈(0,?)单调递减,
见右图。
总结: 当遇到三次或三次以上的,或图象很难
画出的函数求单调性问题时,应考虑导数法。
1°什么情况下,用“导数法” 求函数单调性、
单调区间较简便?
作业:书P26-练习1
P31-习题1.3A组1、2
青海油田第一中学
授课内容:函数的单调性与导数
4、对数函数的导数:
5、指数函数的导数:
3、三角函数 :
1、常函数:(C)′? (c为常数);
2、幂函数 : (xn)′?
课 前 热 身
6、求下列函数的导数:
0
nxn?1
高二数学选修2-2第一章- -导数及其应用之
函数 y = f (x) 在给定区间 G 上,任取 x 1、x 2 ∈G 且 x 1< x 2 ,
1)都有 f ( x 1 ) < f ( x 2 ),
则 f ( x ) 在G 上是增函数;
2)都有 f ( x 1 ) > f ( x 2 ),
则 f ( x ) 在G 上是减函数;
若 f(x) 在G上是增函数或减函数,
则 f(x) 在G上具有严格的单调性.
G 称为单调区间
G = ( a , b )
一、复习引入
判断函数单调性有哪些方法?
图象法
减
增
如图:
思考:那么如何求出下列函数的单调性呢?
(1)f(x)=2x3-6x2+7 (2)f(x)=ex-x+1 (3)f(x)=sinx-x
发现问题:用单调性定义讨论函数单调性虽然
可行,但十分麻烦,尤其是在不知道函数图象
时。例如:2x3-6x2+7,是否有更为简捷的方法
呢?下面我们通过函数图象与导函数的正负来考察单调性与导数有什么关系。
x
y
O
x
y
O
x
y
O
x
y
O
y = x
y = x2
y = x3
观察下面一些函数的图象, 探讨函数的单调性与其导函数正负的关系.
如果在某个区间内恒有f?(x)=0,则f(x)为常数函数
如果恒有f′(x)>0,
则 y=f(x)在这个区间(a,b)内单调递增;
如果恒有 f′(x)<0,
则y=f(x)在这个区间(a,b)内单调递减。
注意:应正确理解 “ 某个区间 ” 的含义,它必是定义域内的某个区间。
例1、已知导函数 的下列信息:
当1
当x>4,或x<1时, <0;
当x=4,或x=1时, =0.试画出函数f(x)图象
的大致形状。
临界点
临界点
三、导数的应用:
C
变式
求函数 的单调区间。
理解训练:
注意:单调区间不可以并起来.
利用导数求函数单调区间的步骤:
说明:函数的单调区间一定是它的定义域的子区间,故求函数的单调区间一定首先要确定函数的定义域,在求出使导数的值为正或负的x的范围时,要与定义域求两者的交集.
变式、判断下列函数的单调性,并求出
单调区间:
(1) f(x)=x3+3x ;
从而函数f(x)=x3+3x
在x∈R上单调递增,
见右图。
(2) f(x)=sinx-x ; x∈(0,p)
从而函数f(x)=sinx-x
在x∈(0,?)单调递减,
见右图。
总结: 当遇到三次或三次以上的,或图象很难
画出的函数求单调性问题时,应考虑导数法。
1°什么情况下,用“导数法” 求函数单调性、
单调区间较简便?
作业:书P26-练习1
P31-习题1.3A组1、2
