1.3.3 导数的实际应用 课件 17张PPT
文档属性
| 名称 | 1.3.3 导数的实际应用 课件 17张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 495.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-07 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
1.4导数的实际应用
规格(L) 2 1.25 0.6
价格(元) 5.1 4.5 2.5
新课导入:下面是某品牌饮料的三种规格不同的产品,若它们的价格如下表所示,则
(1)对消费者而言,选择哪一种更合算呢?
(2)对制造商而言,哪一种的利润更大?
生活中经常遇到求利润最大、用料最省、效率最高等问题,这些问题通常称为优化问题.
我们知道,导数是求函数最大(小)值的有力工具,本节我们运用导数,解决一些生活中的优化问题.
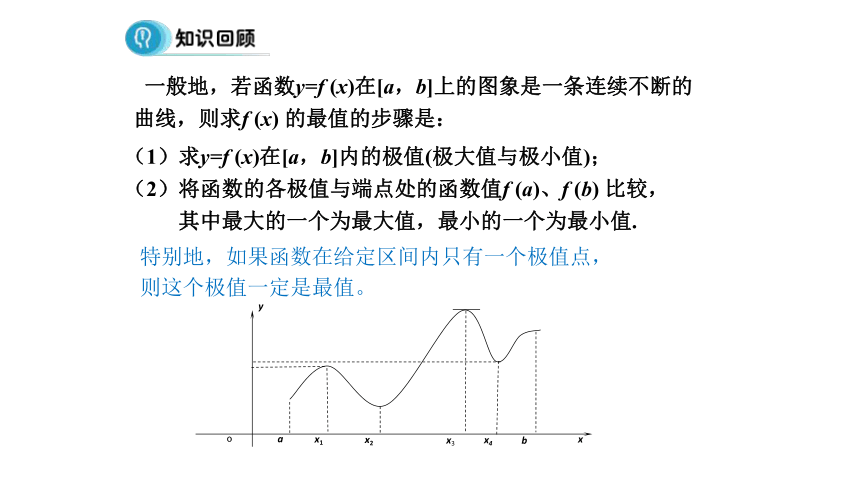
一般地,若函数y=f (x)在[a,b]上的图象是一条连续不断的
曲线,则求f (x) 的最值的步骤是:
(1)求y=f (x)在[a,b]内的极值(极大值与极小值);
(2)将函数的各极值与端点处的函数值f (a)、f (b) 比较,
其中最大的一个为最大值,最小的一个为最小值.
特别地,如果函数在给定区间内只有一个极值点,
则这个极值一定是最值。
y
o
a
x1
x2
x3
x4
b
x
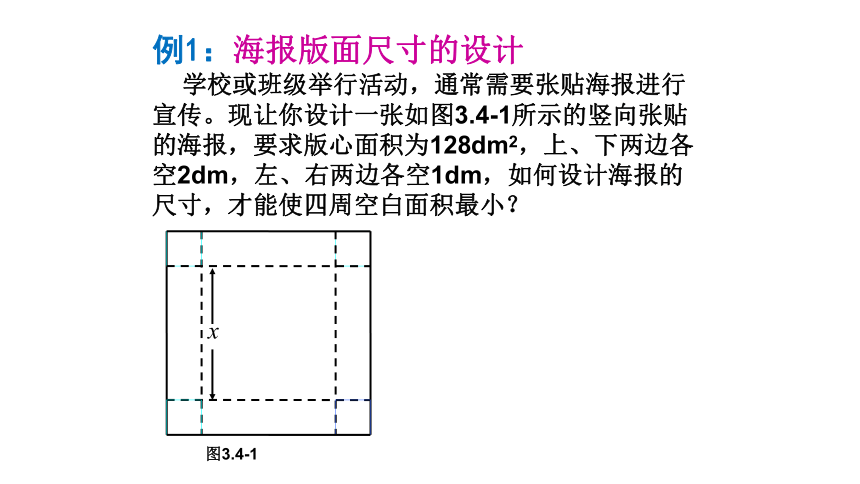
例1:海报版面尺寸的设计
学校或班级举行活动,通常需要张贴海报进行宣传。现让你设计一张如图3.4-1所示的竖向张贴的海报,要求版心面积为128dm2,上、下两边各空2dm,左、右两边各空1dm,如何设计海报的尺寸,才能使四周空白面积最小?
图3.4-1
因此,x=16是函数S(x)的极小值,也是最小值点。所以,
当版心高为16dm,宽为8dm时,能使四周空白面积最小。
解法二:由解法(一)得
2.在实际应用题目中,若函数f(x)在定义域内只有一个极值点x0 ,则不需与端点比较,f(x0)即是所求的最大值或最小值.
1.设出变量找出函数关系式;
(所说区间的也适用于开区间或无穷区间)
确定出定义域;
所得结果符合问题的实际意义。
例2:某种圆柱形的饮料罐的容积一定时,如何确定它的高与底半径,使得所用材料最省?
R
h
解 设圆柱的高为h,底面半径为R.
则表面积为 S(R)=2πRh+2πR2.
又V=πR2h(定值),
即h=2R.
可以判断S(R)只有一个极值点,且是最小值点.
答 罐高与底的直径相等时, 所用材料最省.
r (0,2) 2 (2,6]
f '(r) 0
f (r)
-
+
减函数↘
增函数↗
-1.07p
解:由于瓶子的半径为r,所以每瓶饮料的利润是
当半径r>2时,f ’(r)>0它表示 f(r) 单调递增,
即半径越大,利润越高;
当半径r<2时,f ’(r)<0 它表示 f(r) 单调递减,
即半径越大,利润越低.
1.半径为2cm 时,利润最小,这时
表示此种瓶内饮料的利润还不够瓶子的成本,
此时利润是负值。
2.半径为6cm时,利润最大。
图1.4-4
由上述例子,我们不难发现,解决优化问题的基本思路是:
上述解决优化问题的过程是一个典型的数学建模过程。
优化问题
用函数表示的数学问题
用导数解决数学问题
优化问题的答案
练习2:在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底边长为多少时,箱子容积最大?最大容积是多少?
练习1.一条长为 的铁丝截成两段,分别弯成两个正方形,要使两个正方形的面积和最小,两段铁丝的长度分别是多少?
则两个正方形面积和为
1解:设两段铁丝的长度分别为x,l-x,
其中0由问题的实际意义可知:
2解:设箱底边长为x,则箱高h=(60-x)/2.箱子容积
V(x)=x2h=(60x2-x3)/2(0令 ,解得x=0(舍去),x=40.且V(40)=16000.
由题意可知,当x过小(接近0)或过大(接近60)时,箱子的容积很小,因此,16000是最大值.
答:当x=40cm时,箱子容积最大,最大容积是16000cm3.
解决优化问题的一般步骤:
(1)审题:阅读理解文字表达的题意,分清条件和结论,
找出问题的主要关系;
(2)建模:将文字语言转化成数学语言,利用数学知识,
建立相应的数学模型;
(3)解模:把数学问题化归为常规问题,选择合适的数
学方法求解;
(4)对结果进行验证评估,定性定量分析,做出正确的
判断,确定其答案。
注意:实际应用中,准确地列出函数解析式并确定函数的定义域是关键。
1.4导数的实际应用
规格(L) 2 1.25 0.6
价格(元) 5.1 4.5 2.5
新课导入:下面是某品牌饮料的三种规格不同的产品,若它们的价格如下表所示,则
(1)对消费者而言,选择哪一种更合算呢?
(2)对制造商而言,哪一种的利润更大?
生活中经常遇到求利润最大、用料最省、效率最高等问题,这些问题通常称为优化问题.
我们知道,导数是求函数最大(小)值的有力工具,本节我们运用导数,解决一些生活中的优化问题.
一般地,若函数y=f (x)在[a,b]上的图象是一条连续不断的
曲线,则求f (x) 的最值的步骤是:
(1)求y=f (x)在[a,b]内的极值(极大值与极小值);
(2)将函数的各极值与端点处的函数值f (a)、f (b) 比较,
其中最大的一个为最大值,最小的一个为最小值.
特别地,如果函数在给定区间内只有一个极值点,
则这个极值一定是最值。
y
o
a
x1
x2
x3
x4
b
x
例1:海报版面尺寸的设计
学校或班级举行活动,通常需要张贴海报进行宣传。现让你设计一张如图3.4-1所示的竖向张贴的海报,要求版心面积为128dm2,上、下两边各空2dm,左、右两边各空1dm,如何设计海报的尺寸,才能使四周空白面积最小?
图3.4-1
因此,x=16是函数S(x)的极小值,也是最小值点。所以,
当版心高为16dm,宽为8dm时,能使四周空白面积最小。
解法二:由解法(一)得
2.在实际应用题目中,若函数f(x)在定义域内只有一个极值点x0 ,则不需与端点比较,f(x0)即是所求的最大值或最小值.
1.设出变量找出函数关系式;
(所说区间的也适用于开区间或无穷区间)
确定出定义域;
所得结果符合问题的实际意义。
例2:某种圆柱形的饮料罐的容积一定时,如何确定它的高与底半径,使得所用材料最省?
R
h
解 设圆柱的高为h,底面半径为R.
则表面积为 S(R)=2πRh+2πR2.
又V=πR2h(定值),
即h=2R.
可以判断S(R)只有一个极值点,且是最小值点.
答 罐高与底的直径相等时, 所用材料最省.
r (0,2) 2 (2,6]
f '(r) 0
f (r)
-
+
减函数↘
增函数↗
-1.07p
解:由于瓶子的半径为r,所以每瓶饮料的利润是
当半径r>2时,f ’(r)>0它表示 f(r) 单调递增,
即半径越大,利润越高;
当半径r<2时,f ’(r)<0 它表示 f(r) 单调递减,
即半径越大,利润越低.
1.半径为2cm 时,利润最小,这时
表示此种瓶内饮料的利润还不够瓶子的成本,
此时利润是负值。
2.半径为6cm时,利润最大。
图1.4-4
由上述例子,我们不难发现,解决优化问题的基本思路是:
上述解决优化问题的过程是一个典型的数学建模过程。
优化问题
用函数表示的数学问题
用导数解决数学问题
优化问题的答案
练习2:在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底边长为多少时,箱子容积最大?最大容积是多少?
练习1.一条长为 的铁丝截成两段,分别弯成两个正方形,要使两个正方形的面积和最小,两段铁丝的长度分别是多少?
则两个正方形面积和为
1解:设两段铁丝的长度分别为x,l-x,
其中0
2解:设箱底边长为x,则箱高h=(60-x)/2.箱子容积
V(x)=x2h=(60x2-x3)/2(0
由题意可知,当x过小(接近0)或过大(接近60)时,箱子的容积很小,因此,16000是最大值.
答:当x=40cm时,箱子容积最大,最大容积是16000cm3.
解决优化问题的一般步骤:
(1)审题:阅读理解文字表达的题意,分清条件和结论,
找出问题的主要关系;
(2)建模:将文字语言转化成数学语言,利用数学知识,
建立相应的数学模型;
(3)解模:把数学问题化归为常规问题,选择合适的数
学方法求解;
(4)对结果进行验证评估,定性定量分析,做出正确的
判断,确定其答案。
注意:实际应用中,准确地列出函数解析式并确定函数的定义域是关键。
