3.1.2 复数的概念 课件 23张PPT
文档属性
| 名称 | 3.1.2 复数的概念 课件 23张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 767.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-07 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
人教B版选修2-2 第三章第一节
3.1.1数系的扩充和
复数的概念
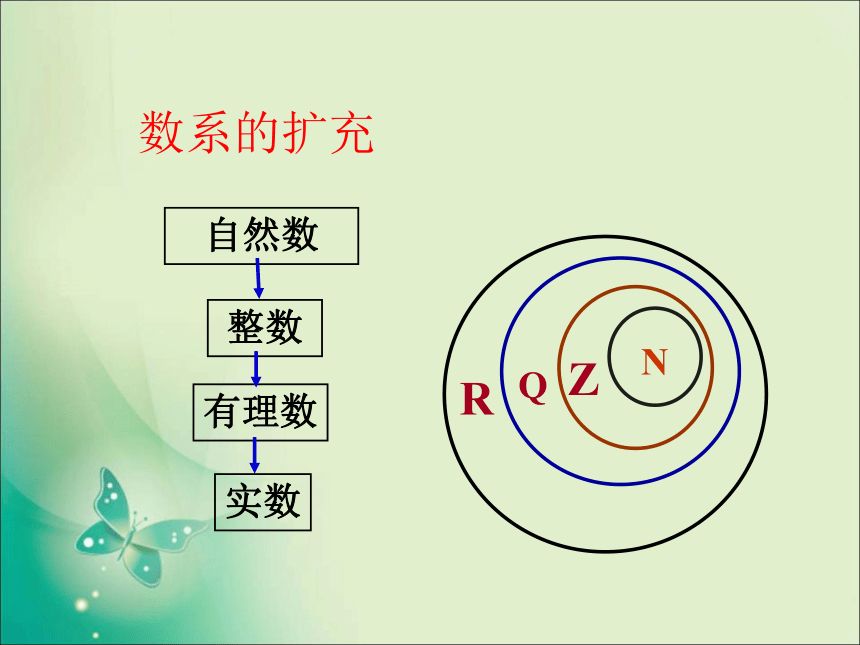
数系的扩充
自然数
自然数
自然数是“数”出来的,其历史最早可以追溯到五万年前.
负数
负数是“欠”出来的.它是由于借贷关系中量的不同意义而产生的.我国三国时期数学家刘徽(公元250年前后)首先给出了负数的定义、记法和加减运算法则.
刘徽(公元250年前后)
分数(有理数)
分数(有理数)是“分”出来的.早在古希腊时期,人类已经对有理数有了非常清楚的认识,而且他们认为有理数就是所有的数.
无理数
毕达哥拉斯(约公元前560——480年)
无理数是“推”出来的.公元前六世纪,古希腊毕达哥拉斯学派利用毕达哥拉斯定理,发现了“无理数”. “无理数”的承认(公元前4世纪)是数学发展史上的一个里程碑.
从社会生活来看为了满足生活和生产实践的需要,数的概念在不断地发展.
从数学内部来看,数集是在按某种 “规则”不断扩充的.
1545年,卡尔丹引入负数的平方根;
1637年,笛卡儿给出“虚数”的名称;
1777年,欧拉首次使用符号i表示-1的平方根;
1830年,高斯把复数与几何(向量)对应起来从而赋予复数几何上的解释
复数的起源
i 的引入
引入一个新数:
虚数单位 i
(2)实数可以与它进行四则运算,进行四则
运算时,原有的加、乘运算律仍然成立.
复数的概念
形如a+bi(a,b∈R)的数叫做复数.
(其中i是虚数单位).
全体复数所成的集合叫做复数集,用C表示
复数的代数形式
通常用字母 z 表示,即
例题讲解
例1:指出下列复数的实部和虚部
复数的相关概念
例题讲解
例2
思 考
复数集与实数集、虚数集、纯虚数集
之间有什么关系?
复数集
虚数集
实数集
纯虚数集
复数相等
两个虚数只能说相等或不相等,而不能比较大小
例题讲解
例3:已知 ,其中 ,
求 。
内容小结
虚数单位
复数概念
复数的代数形式
复数的分类
复数相等
作业布置
必做:课本P104 练习题1,2,3
选做:优化 基础巩固 全部
人教B版选修2-2 第三章第一节
3.1.1数系的扩充和
复数的概念
数系的扩充
自然数
自然数
自然数是“数”出来的,其历史最早可以追溯到五万年前.
负数
负数是“欠”出来的.它是由于借贷关系中量的不同意义而产生的.我国三国时期数学家刘徽(公元250年前后)首先给出了负数的定义、记法和加减运算法则.
刘徽(公元250年前后)
分数(有理数)
分数(有理数)是“分”出来的.早在古希腊时期,人类已经对有理数有了非常清楚的认识,而且他们认为有理数就是所有的数.
无理数
毕达哥拉斯(约公元前560——480年)
无理数是“推”出来的.公元前六世纪,古希腊毕达哥拉斯学派利用毕达哥拉斯定理,发现了“无理数”. “无理数”的承认(公元前4世纪)是数学发展史上的一个里程碑.
从社会生活来看为了满足生活和生产实践的需要,数的概念在不断地发展.
从数学内部来看,数集是在按某种 “规则”不断扩充的.
1545年,卡尔丹引入负数的平方根;
1637年,笛卡儿给出“虚数”的名称;
1777年,欧拉首次使用符号i表示-1的平方根;
1830年,高斯把复数与几何(向量)对应起来从而赋予复数几何上的解释
复数的起源
i 的引入
引入一个新数:
虚数单位 i
(2)实数可以与它进行四则运算,进行四则
运算时,原有的加、乘运算律仍然成立.
复数的概念
形如a+bi(a,b∈R)的数叫做复数.
(其中i是虚数单位).
全体复数所成的集合叫做复数集,用C表示
复数的代数形式
通常用字母 z 表示,即
例题讲解
例1:指出下列复数的实部和虚部
复数的相关概念
例题讲解
例2
思 考
复数集与实数集、虚数集、纯虚数集
之间有什么关系?
复数集
虚数集
实数集
纯虚数集
复数相等
两个虚数只能说相等或不相等,而不能比较大小
例题讲解
例3:已知 ,其中 ,
求 。
内容小结
虚数单位
复数概念
复数的代数形式
复数的分类
复数相等
作业布置
必做:课本P104 练习题1,2,3
选做:优化 基础巩固 全部
