3.1.2 复数的概念 课件 26张PPT
文档属性
| 名称 | 3.1.2 复数的概念 课件 26张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-07 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
提出问题:
结论:此方程没有实数根.
解一元二次方程
希望:此方程有解!
实数不够用!
矛盾!
如何解决?
无理数
实数(R)
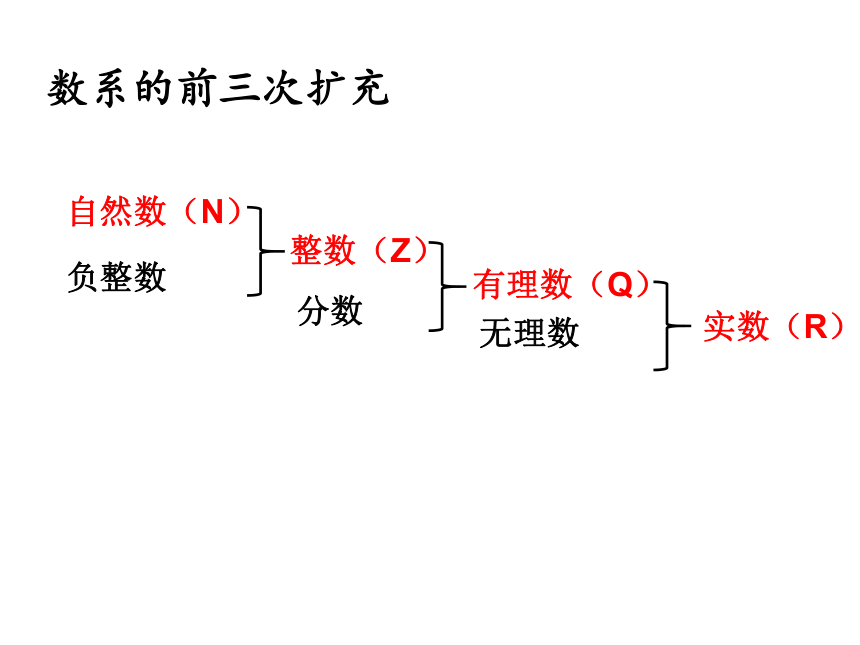
数系的前三次扩充
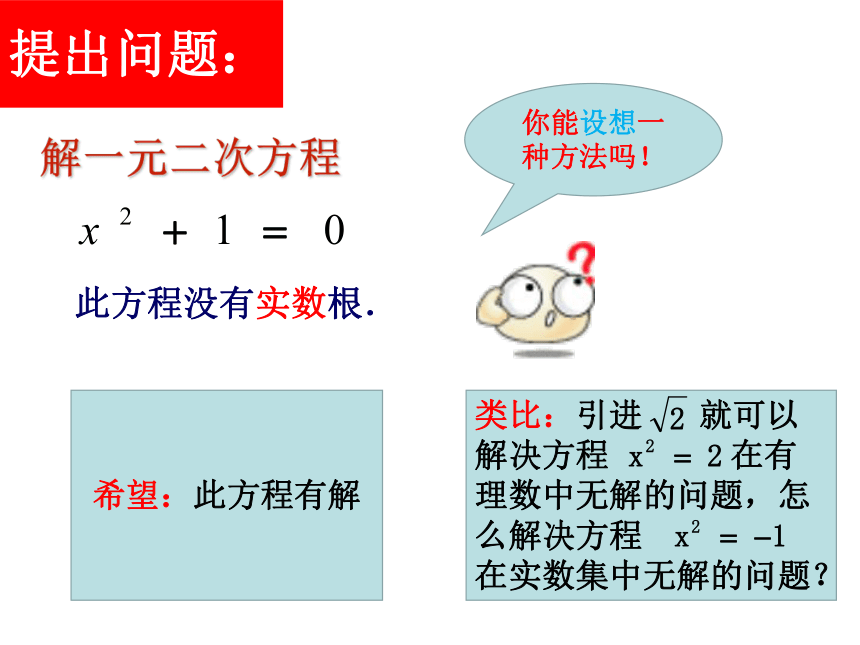
提出问题:
此方程没有实数根.
解一元二次方程
希望:此方程有解
解决问题:
在数学大师的引导下,大胆引入 虚数单位” ”,
规定:
(1) ;
(2)实数可以与i进行四则运算,进行四则运算时,原有的加法、乘法运算律仍然成立.
试一试:
请大家给出实数与虚数单位i进行加法、乘法运算的式子
1.复数的概念:形如a+bi(a,b∈R)的数叫做复数.
全体复数所形成的集合叫做复数集,一般用字母C表示 .
2、复数的代数形式:
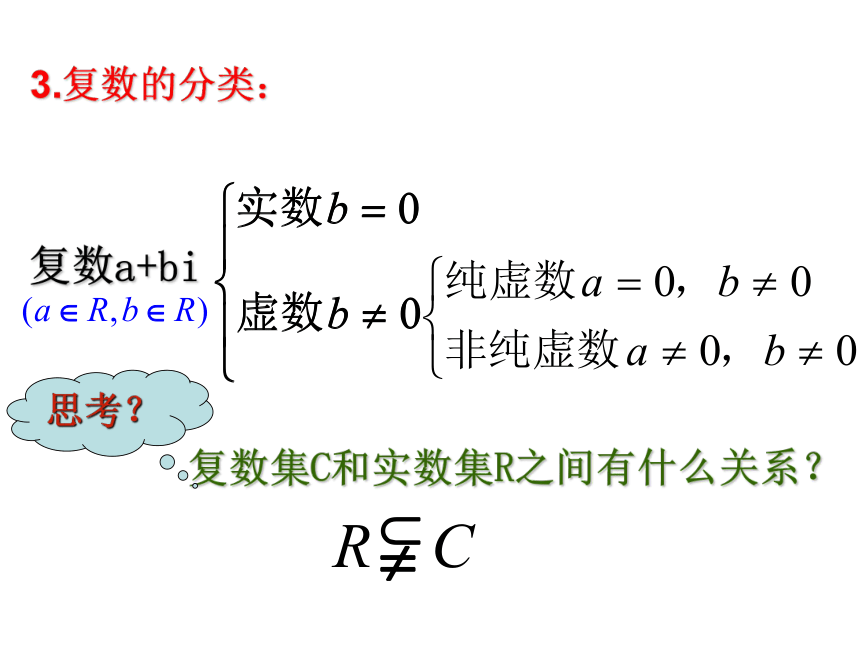
3.复数的分类:
1.说明下列数中,哪些是实数,哪些是虚数,哪些是纯虚数,并指出复数的实部与虚部.
例1: 实数m取什么值时,复数
(1)实数? (2)虚数?(3)纯虚数?
【题后总结】处理有关复数概念的问题,应找准实部、虚部,非代数形式,通过运算化为代数形式再应用定义求解
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
4.复数相等的充要条件:
解:根据复数相等的定义,得方程组
【题后总结】复数相等问题,提供了复数问题转化为实数问题的依据,这是解复数问题常用的思想方法
三、课堂小结:
1.知识方面的收获?
2.思想方法方面的收获?
3.还有其他的疑问吗?
中国是世界上最早认识应用负数的国家. 早在2000多年前的《九章算术》中,就有正数和负数的记载. 在古代人民生活中,以收入钱为正,以支出钱为负,在粮食生产中,以产量增加为正,以产量减少为负. 古代的人们为区分正数、负数,常用红色的算筹表示正,黑色的算筹表示负.
数的发展史------整数
自然数(N)
负整数
整数(Z)
分数的产生经历了一个漫长的过程. 开始人们只使用简单的分数,如一半,一半的一半等. 大约在2000年前,古希腊人已经开始用分子和分母表示分数. 后来,阿拉伯人发明了分数线,分数的表示法就成为现在的样子了.
数的发展史------有理数
分数
有理数(Q)
公元前6世纪末,毕达哥拉斯学派认为宇宙间的一切都可以归结为整数和整数之比(有理数),但其中一个学生希帕索斯提出问题:边长为1的正方形对角线的长度是多少?
数的发展史------实数
无理数
实数(R)
x
数的发展史反思
(2)数系是怎样扩充的(原则)?
(1)人们为什么要不断扩充数系?
(3)扩充前后的数集之间有何关系?
数系扩充的原则
1.从数系A扩充到数系B必须满足A是B的真子集;
2.数系A中定义了的基本运算能扩展为数系B的运算;
3.A中不是永远可行的某种运算,在B中永远可行,例如,自然数系扩充为整数系后,减法的运算就能施行;
4.B是满足上述条件的惟一的最小的扩充,例如,自然数系只能扩充为整数系,而不能一下扩展为实数系。
提出问题:
结论:此方程没有实数根.
解一元二次方程
希望:此方程有解!
实数不够用!
矛盾!
如何解决?
无理数
实数(R)
数系的前三次扩充
提出问题:
此方程没有实数根.
解一元二次方程
希望:此方程有解
解决问题:
在数学大师的引导下,大胆引入 虚数单位” ”,
规定:
(1) ;
(2)实数可以与i进行四则运算,进行四则运算时,原有的加法、乘法运算律仍然成立.
试一试:
请大家给出实数与虚数单位i进行加法、乘法运算的式子
1.复数的概念:形如a+bi(a,b∈R)的数叫做复数.
全体复数所形成的集合叫做复数集,一般用字母C表示 .
2、复数的代数形式:
3.复数的分类:
1.说明下列数中,哪些是实数,哪些是虚数,哪些是纯虚数,并指出复数的实部与虚部.
例1: 实数m取什么值时,复数
(1)实数? (2)虚数?(3)纯虚数?
【题后总结】处理有关复数概念的问题,应找准实部、虚部,非代数形式,通过运算化为代数形式再应用定义求解
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
4.复数相等的充要条件:
解:根据复数相等的定义,得方程组
【题后总结】复数相等问题,提供了复数问题转化为实数问题的依据,这是解复数问题常用的思想方法
三、课堂小结:
1.知识方面的收获?
2.思想方法方面的收获?
3.还有其他的疑问吗?
中国是世界上最早认识应用负数的国家. 早在2000多年前的《九章算术》中,就有正数和负数的记载. 在古代人民生活中,以收入钱为正,以支出钱为负,在粮食生产中,以产量增加为正,以产量减少为负. 古代的人们为区分正数、负数,常用红色的算筹表示正,黑色的算筹表示负.
数的发展史------整数
自然数(N)
负整数
整数(Z)
分数的产生经历了一个漫长的过程. 开始人们只使用简单的分数,如一半,一半的一半等. 大约在2000年前,古希腊人已经开始用分子和分母表示分数. 后来,阿拉伯人发明了分数线,分数的表示法就成为现在的样子了.
数的发展史------有理数
分数
有理数(Q)
公元前6世纪末,毕达哥拉斯学派认为宇宙间的一切都可以归结为整数和整数之比(有理数),但其中一个学生希帕索斯提出问题:边长为1的正方形对角线的长度是多少?
数的发展史------实数
无理数
实数(R)
x
数的发展史反思
(2)数系是怎样扩充的(原则)?
(1)人们为什么要不断扩充数系?
(3)扩充前后的数集之间有何关系?
数系扩充的原则
1.从数系A扩充到数系B必须满足A是B的真子集;
2.数系A中定义了的基本运算能扩展为数系B的运算;
3.A中不是永远可行的某种运算,在B中永远可行,例如,自然数系扩充为整数系后,减法的运算就能施行;
4.B是满足上述条件的惟一的最小的扩充,例如,自然数系只能扩充为整数系,而不能一下扩展为实数系。
