2.3 二次函数与一元二次方程、不等式课件(42张ppt)共两课时
文档属性
| 名称 | 2.3 二次函数与一元二次方程、不等式课件(42张ppt)共两课时 |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-06 14:53:03 | ||
图片预览











文档简介
课件42张PPT。2.2.3 二次函数与一元二次方程、不等式(共2课时)
(第1课时)
第二章 一元二次函数、方程和不等式情境导学问题 园艺师打算在绿地上用栅栏围一个矩形区域种植花卉.若栅栏的长度是24m,围成的矩形区域的面积要大于20m2,则这个矩形的边长为多少米?
情境导学设这个矩形的一条边长为xm,则另一条边长为(12-x)m.
由题意,得:(12-x)x>20,
其中x∈{x|0<x<12}. 整理得
x2-12x+20<0,x∈{x|0<x<12}. ①
求得不等式①的解集,就得到了问题的答案. 我们把只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式.一元二次不等式的定义: 一元二次不等式的一般表达式ax2+bx+c>0 (a≠0)
或ax2+bx+c<0 (a≠0),其中a,b,c均为常数.概念解析画出二次函数 的图象.当 时,y>0.yx=0或5y=x2-5x探究1 一元二次不等式的解法方程 的根为:0,5 当 时,y=0.当 时,y<0. 由图象可知:
不等式 的解集为 ;
不等式 的解集为 . 新知探究不等式
的解集是什么?小组活动:
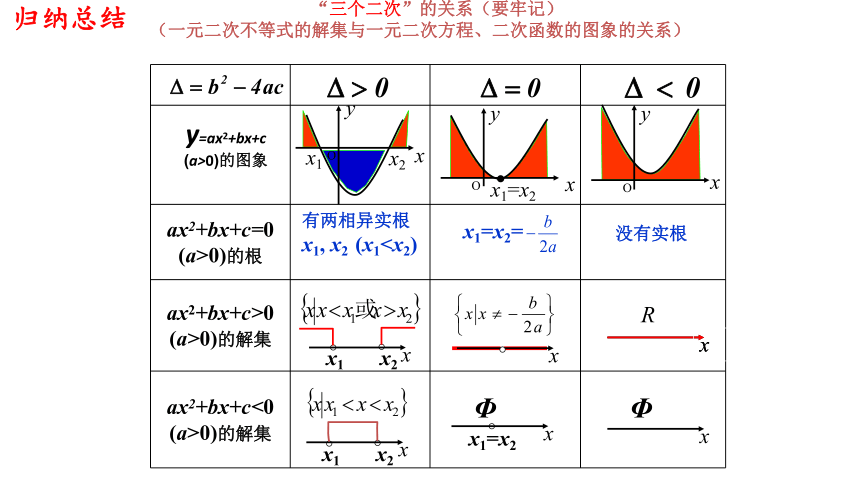
1、仿照上述过程讨论填写“三个二次”之间的关系表格。
2、讨论总结在这个过程中用到了哪些数学思想和数学方法?新知探究没有实根y=ax2+bx+c
(a>0)的图象有两相异实根
x1, x2 (x1(一元二次不等式的解集与一元二次方程、二次函数的图象的关系)归纳总结华罗庚教授说过:
数缺形时少直观
形少数时难入微
数形结合百般好
隔离分家万事非归纳总结例1:解不等式: x2-2x-15≥0 原不等式变形为(x+3)(x-5) ≥ 0 方程(x+3)(x-5)=0的
两根为: x=-3,或x=5∴ 不等式的解集
为:{x│ x ≤-3 或x ≥5}。解:典例解析例2:解不等式- x2 + 2x – 3 >0 解:整理,得 x2 - 2x + 3 < 0因为△= 4 - 12 = - 8 < 0方程 2 x2 - 3x – 2 = 0无实数根所以原不等式的解集为ф【点评】 若a<0时,先二次项系数化正!典例解析解:典例解析
结合以上例题总结:
1、求解一元二次不等式的步骤是什么?
2、解一元二次不等式中常见的错误是什么?应如何避免?
归纳总结 (1)二次项的系数变为正 (a>0)
(2) 看能否因式分解,不能分解的计算△,
(3) 求出方程ax2+bx+c=0 的实根;(画出函数图像)
(4)(结合函数图象)写出不等式的解集.解一元二次不等式ax2+bx+c>0、ax2+bx+c<0 (a>0)的步骤: 归纳总结思维导图1.不等式2x2-x-1>0的解集是√当堂达标∵2x2-x-1=(2x+1)(x-1),
∴由2x2-x-1>0,得(2x+1)(x-1)>0,
1234当堂达标2.不等式-6x2-x+2≤0的解集是√1234∵-6x2-x+2≤0,∴6x2+x-2≥0,
∴(2x-1)(3x+2)≥0,∴x≥ 或x≤ .当堂达标当堂达标4.若不等式ax2+8ax+21<0的解集是{x|-7∴-7×(-1)= ,故a=3.当堂达标5.若不等式(a-2)x2+2(a-2)x-4<0的解集为R,求实数a的取值范围.当a-2=0,即a=2时,原不等式为-4<0,
所以a=2时解集为R.
1234解得-20);(2)计算判别式,判断方程是否有根;(3)如果有根,求出方程的根;(4)写出不等式的解集,大于取两边、小于取中间。3.数学思想方法:1.“三个二次”的关系一、知识上我收获了什么?二、方法上我收获了什么?数形结合、分类讨论、转化与化归课堂小结2.2.3 二次函数与一元二次方程、不等式
(第2课时) 小试牛刀典例解析例1 一家车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量x(单位:辆)与创造的价值y(单位:元)之间有如下的关系:y=-2x2+220x.
若这家工厂希望在一个星期内利用这条流水线创收6000元以上,则在一个星期内大约应该生产多少辆摩托车?解:设这家工厂在一个星期内大约应该利用这条流水线生产x辆摩托车,根据题意,
得-2x2+220x>6000.
移项整理,得x2 -110x+3000<0.
对于方程x2 -110x+3000=0,
Δ=100>0,
方程有两个实数根x1=50,x2=60.画出二次函数y=x2 -110x+3000的图象
结合图象得不等式x2 -110x+3000<0
的解集为{x|50<x<60},
从而原不等式的解集为{x|50<x<60}.
因为狓只能取整数值,所以当这条流水线在一周内生产的摩托车
数量在51~59辆时,这家工厂能够获得6000元以上的收益.跟踪训练?典例解析?跟踪训练归纳总结当堂达标1.解一元二次不等式的一般步骤是:
(1)化为标准形式;
(2)确定判别式Δ=b2-4ac的符号;
(3)若Δ≥0,则求出该不等式对应的二次方程的根;若Δ<0,则对应的二次方程无根;
(4)联系二次函数的图象得出不等式的解集.特别地,若一元二次不等式的左边的二次三项式能分解因式,则可立即写出不等式的解集(在两根之内或两根之外).课堂小结
(第1课时)
第二章 一元二次函数、方程和不等式情境导学问题 园艺师打算在绿地上用栅栏围一个矩形区域种植花卉.若栅栏的长度是24m,围成的矩形区域的面积要大于20m2,则这个矩形的边长为多少米?
情境导学设这个矩形的一条边长为xm,则另一条边长为(12-x)m.
由题意,得:(12-x)x>20,
其中x∈{x|0<x<12}. 整理得
x2-12x+20<0,x∈{x|0<x<12}. ①
求得不等式①的解集,就得到了问题的答案. 我们把只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式.一元二次不等式的定义: 一元二次不等式的一般表达式ax2+bx+c>0 (a≠0)
或ax2+bx+c<0 (a≠0),其中a,b,c均为常数.概念解析画出二次函数 的图象.当 时,y>0.yx=0或5y=x2-5x探究1 一元二次不等式的解法方程 的根为:0,5 当 时,y=0.当 时,y<0. 由图象可知:
不等式 的解集为 ;
不等式 的解集为 . 新知探究不等式
的解集是什么?小组活动:
1、仿照上述过程讨论填写“三个二次”之间的关系表格。
2、讨论总结在这个过程中用到了哪些数学思想和数学方法?新知探究没有实根y=ax2+bx+c
(a>0)的图象有两相异实根
x1, x2 (x1
数缺形时少直观
形少数时难入微
数形结合百般好
隔离分家万事非归纳总结例1:解不等式: x2-2x-15≥0 原不等式变形为(x+3)(x-5) ≥ 0 方程(x+3)(x-5)=0的
两根为: x=-3,或x=5∴ 不等式的解集
为:{x│ x ≤-3 或x ≥5}。解:典例解析例2:解不等式- x2 + 2x – 3 >0 解:整理,得 x2 - 2x + 3 < 0因为△= 4 - 12 = - 8 < 0方程 2 x2 - 3x – 2 = 0无实数根所以原不等式的解集为ф【点评】 若a<0时,先二次项系数化正!典例解析解:典例解析
结合以上例题总结:
1、求解一元二次不等式的步骤是什么?
2、解一元二次不等式中常见的错误是什么?应如何避免?
归纳总结 (1)二次项的系数变为正 (a>0)
(2) 看能否因式分解,不能分解的计算△,
(3) 求出方程ax2+bx+c=0 的实根;(画出函数图像)
(4)(结合函数图象)写出不等式的解集.解一元二次不等式ax2+bx+c>0、ax2+bx+c<0 (a>0)的步骤: 归纳总结思维导图1.不等式2x2-x-1>0的解集是√当堂达标∵2x2-x-1=(2x+1)(x-1),
∴由2x2-x-1>0,得(2x+1)(x-1)>0,
1234当堂达标2.不等式-6x2-x+2≤0的解集是√1234∵-6x2-x+2≤0,∴6x2+x-2≥0,
∴(2x-1)(3x+2)≥0,∴x≥ 或x≤ .当堂达标当堂达标4.若不等式ax2+8ax+21<0的解集是{x|-7
所以a=2时解集为R.
1234解得-2
(第2课时) 小试牛刀典例解析例1 一家车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量x(单位:辆)与创造的价值y(单位:元)之间有如下的关系:y=-2x2+220x.
若这家工厂希望在一个星期内利用这条流水线创收6000元以上,则在一个星期内大约应该生产多少辆摩托车?解:设这家工厂在一个星期内大约应该利用这条流水线生产x辆摩托车,根据题意,
得-2x2+220x>6000.
移项整理,得x2 -110x+3000<0.
对于方程x2 -110x+3000=0,
Δ=100>0,
方程有两个实数根x1=50,x2=60.画出二次函数y=x2 -110x+3000的图象
结合图象得不等式x2 -110x+3000<0
的解集为{x|50<x<60},
从而原不等式的解集为{x|50<x<60}.
因为狓只能取整数值,所以当这条流水线在一周内生产的摩托车
数量在51~59辆时,这家工厂能够获得6000元以上的收益.跟踪训练?典例解析?跟踪训练归纳总结当堂达标1.解一元二次不等式的一般步骤是:
(1)化为标准形式;
(2)确定判别式Δ=b2-4ac的符号;
(3)若Δ≥0,则求出该不等式对应的二次方程的根;若Δ<0,则对应的二次方程无根;
(4)联系二次函数的图象得出不等式的解集.特别地,若一元二次不等式的左边的二次三项式能分解因式,则可立即写出不等式的解集(在两根之内或两根之外).课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
