人教新课标A版 选修4-5 第一讲1.1.1 不等式的基本性质(27张PPT)
文档属性
| 名称 | 人教新课标A版 选修4-5 第一讲1.1.1 不等式的基本性质(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 631.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-07 00:00:00 | ||
图片预览






文档简介
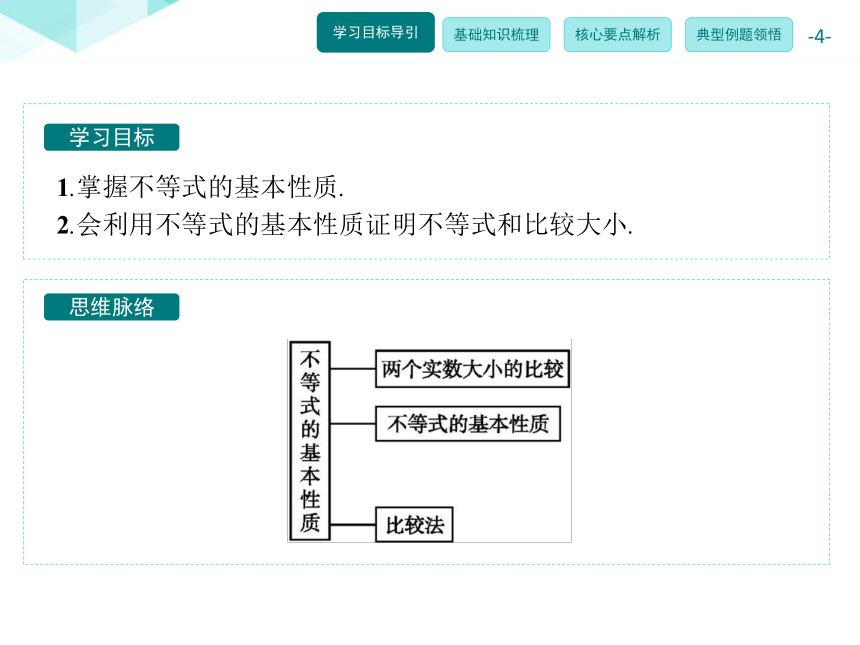
课件27张PPT。第一讲 不等式和绝对值不等式一 不等式1.不等式的基本性质学习目标思维脉络1.掌握不等式的基本性质.
2.会利用不等式的基本性质证明不等式和比较大小.知识清单预习自测1.两个实数大小的比较
(1)a>b ?a-b>0;
(2)a=b ?a-b=0;
(3)a2.不等式的基本性质
(1)如果a>b,那么bb,即a>b?b(2)如果a>b,b>c,那么a>c,即a>b,b>c ?a>c.
(3)如果a>b,那么a+c>b+c.
(4)如果a>b,c>0,那么ac>bc;如果a>b,c<0,那么ac(5)如果a>b>0,那么an>bn(n∈N,n≥2).3.作差比较法
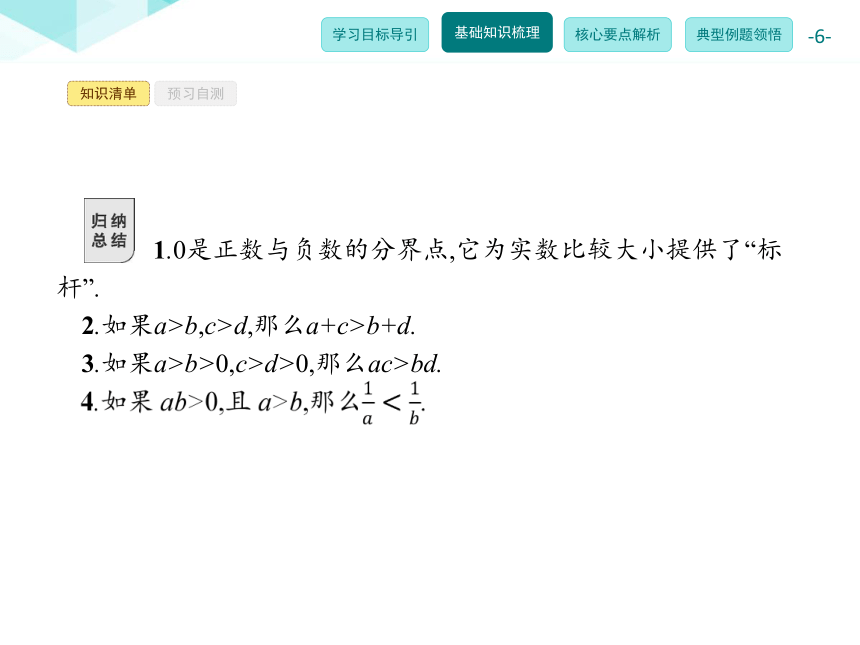
(1)理论依据:a-b>0?a>b;a-b=0?a=b;a-b<0?a(2)方法步骤:① 作差;② 变形;③ 判断符号;④ 下结论.知识清单预习自测 1.0是正数与负数的分界点,它为实数比较大小提供了“标杆”.
2.如果a>b,c>d,那么a+c>b+d.
3.如果a>b>0,c>d>0,那么ac>bd.12345知识清单预习自测1.若a>b,则下列不等式一定成立的是( ) C.-a>-b D.a-b>0
答案:D12345知识清单预习自测2.“a+c>b+d”是“a>b,且c>d”的( )
A.必要不充分条件
B.充分不必要条件
C.充要条件
D.既不充分也不必要条件
解析:∵a+c>b+d?/ a>b,且c>d,但a>b,且c>d?a+c>b+d,
∴“a+c>b+d”是“a>b,且c>d”的必要不充分条件.
答案:A12345知识清单预习自测3.若a<0,-1A.a>ab>ab2 B.ab2>ab>a
C.ab>a>ab2 D.ab>ab2>a
解析:∵a<0,-10,ab2<0,故排除A,B选项.又0a.故选D.
答案:D12345知识清单预习自测由已知可得a>0,b>0,且ab<1,
∴1-ab>0,∴M-N>0,即M>N.又M>0,N>0,∴M>N.
答案:M>N12345知识清单预习自测5.设x=a2b2+5,y=2ab-a2-4a,若x>y,则实数a,b满足的条件是 .?
解析:x-y=(ab-1)2+(a+2)2.因为x>y,所以(ab-1)2+(a+2)2>0,
所以ab-1≠0或a+2≠0,即ab≠1或a≠-2.
答案:ab≠1或a≠-2121.使用不等式的性质要注意的问题
剖析:(1)在应用传递性时,如果两个不等式中有一个带等号而另一个不带等号,那么等号是传递不过去的.如a≤b,bb?ac2>bc2;若无c≠0这个条件,则a>b?ac2>bc2就是错误结论(当c=0时,取“=”).(3)a>b>0?an>bn>0成立的条件是“n为大于0的数”,如果去掉“n为大于0的数”这个条件,取n=-1,a=3,b=2,那么就会出现3-1>2-1,即
的错误结论.122.不等式性质中的“?”和“?”表示的意思
剖析:在不等式的基本性质中,条件和结论的逻辑关系有两种:“?”与“?”,即推出关系和等价关系,或者说“不可逆关系”与“可逆关系”.这就要求必须熟记与区别不同性质的条件.题型一题型二题型三题型四不等式的基本性质
【例1】 若a,b,c∈R,a>b,则下列不等式成立的是( )解析:本题只提供了“a,b,c∈R,a>b”这个条件,而不等式的基本性质中,几乎都有类似的前提条件,但结论会根据不同的要求有所不同,因而这需要根据本题的四个选项来进行判断.选项A,还需有ab>0这个前提条件;选项B,当a,b都为负数时不成立,或一正一负时答案:C 题型一题型二题型三题型四反思对于考查不等式的基本性质的选择题,解答时,一是利用不等式的相关性质,其中,特别要注意不等号变号的影响因素,如乘数、取倒数、开方、平方等;二是对所含字母取特殊值,结合排除法去选正确的选项,这种方法一般要注意选取的值应具有某个方面的代表性,如选取0、正数、负数等.题型一题型二题型三题型四【变式训练1】 判断下列命题的真假,并简述理由.
(1)若a>b,c>d,则ac>bd;(3)若a>b,cb-d;
(4)若a>b,则an>bn(n∈N,且n≥2).题型一题型二题型三题型四解:(1)假命题.取a=3,b=2,c=-2,d=-3,即3>2,-2>-3,此时ac=bd=-6.因此(1)为假命题.
(2)假命题.因同向不等式不能相除,取a=6,b=4,c=3,d=2,(3)真命题.∵c-d.
又a>b,∴a-c>b-d,因此(3)为真命题.
(4)假命题.当a>b>0时,才能成立,取a=-2,b=-3,当n为偶数时不成立,因此(4)为假命题.题型一题型二题型三题型四用作差法比较大小 分析:比较两个数(式)的大小,将两数(式)作差,若差值为正,则前者大;若差值为负,则后者大.=(a2+1)2-2a2-[(a2+1)2-a2]=-2a2+a2=-a2.
∵a≠0,∴-a2<0.题型一题型二题型三题型四反思1.用作差法比较两个数(式)的大小时,要按照“三步一结论”的步骤进行,即:作差 变形 判断符号结论,其中变形是关键,判断符号是目的.
2.在变形中,一般是变形得越彻底越有利于下一步的判断,变形的常用技巧有:因式分解、配方、通分、分母有理化等.
3.若为几个因式的积,需对每个因式判断符号;当符号不确定时,需进行分类讨论.题型一题型二题型三题型四题型一题型二题型三题型四利用不等式的基本性质求范围
【例3】 已知60∴需先求出-y的取值范围.题型一题型二题型三题型四反思本题不能直接用x的取值范围去减或除以y的取值范围,应严格利用不等式的基本性质去求得取值范围.在有些题目中,还要注意整体代换的思想,即弄清要求与已知“范围”间的联系.题型一题型二题型三题型四【变式训练3】 已知-1易错点 同向不等式相加时,忽视前提条件致错题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四反思求代数式的取值范围需严格依据不等式的性质和运算法则进行运算,这是解答此类问题的基础.在使用不等式的性质时,如果是由两个变量的取值范围求其差的取值范围,那么一定不能直接作差,而要先转化为同向不等式后再求和.
2.会利用不等式的基本性质证明不等式和比较大小.知识清单预习自测1.两个实数大小的比较
(1)a>b ?a-b>0;
(2)a=b ?a-b=0;
(3)a
(1)如果a>b,那么b
(3)如果a>b,那么a+c>b+c.
(4)如果a>b,c>0,那么ac>bc;如果a>b,c<0,那么ac
(1)理论依据:a-b>0?a>b;a-b=0?a=b;a-b<0?a
2.如果a>b,c>d,那么a+c>b+d.
3.如果a>b>0,c>d>0,那么ac>bd.12345知识清单预习自测1.若a>b,则下列不等式一定成立的是( ) C.-a>-b D.a-b>0
答案:D12345知识清单预习自测2.“a+c>b+d”是“a>b,且c>d”的( )
A.必要不充分条件
B.充分不必要条件
C.充要条件
D.既不充分也不必要条件
解析:∵a+c>b+d?/ a>b,且c>d,但a>b,且c>d?a+c>b+d,
∴“a+c>b+d”是“a>b,且c>d”的必要不充分条件.
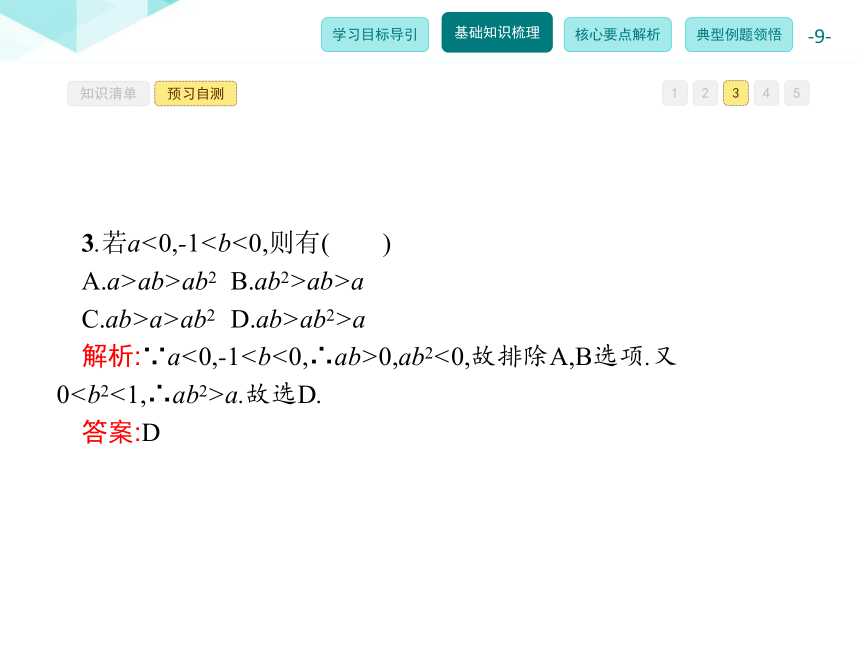
答案:A12345知识清单预习自测3.若a<0,-1
C.ab>a>ab2 D.ab>ab2>a
解析:∵a<0,-1
答案:D12345知识清单预习自测由已知可得a>0,b>0,且ab<1,
∴1-ab>0,∴M-N>0,即M>N.又M>0,N>0,∴M>N.
答案:M>N12345知识清单预习自测5.设x=a2b2+5,y=2ab-a2-4a,若x>y,则实数a,b满足的条件是 .?
解析:x-y=(ab-1)2+(a+2)2.因为x>y,所以(ab-1)2+(a+2)2>0,
所以ab-1≠0或a+2≠0,即ab≠1或a≠-2.
答案:ab≠1或a≠-2121.使用不等式的性质要注意的问题
剖析:(1)在应用传递性时,如果两个不等式中有一个带等号而另一个不带等号,那么等号是传递不过去的.如a≤b,b
的错误结论.122.不等式性质中的“?”和“?”表示的意思
剖析:在不等式的基本性质中,条件和结论的逻辑关系有两种:“?”与“?”,即推出关系和等价关系,或者说“不可逆关系”与“可逆关系”.这就要求必须熟记与区别不同性质的条件.题型一题型二题型三题型四不等式的基本性质
【例1】 若a,b,c∈R,a>b,则下列不等式成立的是( )解析:本题只提供了“a,b,c∈R,a>b”这个条件,而不等式的基本性质中,几乎都有类似的前提条件,但结论会根据不同的要求有所不同,因而这需要根据本题的四个选项来进行判断.选项A,还需有ab>0这个前提条件;选项B,当a,b都为负数时不成立,或一正一负时答案:C 题型一题型二题型三题型四反思对于考查不等式的基本性质的选择题,解答时,一是利用不等式的相关性质,其中,特别要注意不等号变号的影响因素,如乘数、取倒数、开方、平方等;二是对所含字母取特殊值,结合排除法去选正确的选项,这种方法一般要注意选取的值应具有某个方面的代表性,如选取0、正数、负数等.题型一题型二题型三题型四【变式训练1】 判断下列命题的真假,并简述理由.
(1)若a>b,c>d,则ac>bd;(3)若a>b,c
(4)若a>b,则an>bn(n∈N,且n≥2).题型一题型二题型三题型四解:(1)假命题.取a=3,b=2,c=-2,d=-3,即3>2,-2>-3,此时ac=bd=-6.因此(1)为假命题.
(2)假命题.因同向不等式不能相除,取a=6,b=4,c=3,d=2,(3)真命题.∵c
又a>b,∴a-c>b-d,因此(3)为真命题.
(4)假命题.当a>b>0时,才能成立,取a=-2,b=-3,当n为偶数时不成立,因此(4)为假命题.题型一题型二题型三题型四用作差法比较大小 分析:比较两个数(式)的大小,将两数(式)作差,若差值为正,则前者大;若差值为负,则后者大.=(a2+1)2-2a2-[(a2+1)2-a2]=-2a2+a2=-a2.
∵a≠0,∴-a2<0.题型一题型二题型三题型四反思1.用作差法比较两个数(式)的大小时,要按照“三步一结论”的步骤进行,即:作差 变形 判断符号结论,其中变形是关键,判断符号是目的.
2.在变形中,一般是变形得越彻底越有利于下一步的判断,变形的常用技巧有:因式分解、配方、通分、分母有理化等.
3.若为几个因式的积,需对每个因式判断符号;当符号不确定时,需进行分类讨论.题型一题型二题型三题型四题型一题型二题型三题型四利用不等式的基本性质求范围
【例3】 已知60
