人教A版高二数学 函数的极值与导数(48张ppt)
文档属性
| 名称 | 人教A版高二数学 函数的极值与导数(48张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-07 16:21:32 | ||
图片预览







文档简介
(共48张PPT)
高二年级 数学
函数的极值与导数
函数的性质
单调性
函数的单调性
与导数的关系
用导数研究函数单调性的方法
f '(x)>0,函数单调递增;
f '(x)<0,函数单调递减.
1.求导;2.求临界点;3.列表;4.单调区间.
复习回顾
解:f '(x)=3x2+6x-24=3(x+4)(x-2).
x (-∞,-4) -4 (-4,2) 2 (2,+∞)
f '(x) 0 0
f (x)
+
+
f '(x)>0,(x+4)(x-2)>0 即x<-4或x>2;
令 f '(x)=0,解得临界点x=-4,或x=2.
1.求出函数f (x)=x3+3x2-24x-20的单调区间.
复习回顾
解:f '(x)=3x2+6x-24=3(x+4)(x-2).
x (-∞,-4) -4 (-4,2) 2 (2,+∞)
f '(x) 0 0
f (x)
f (x)的单调递增区间为(-∞,-4),(2,+∞).
+
+
-
f '(x)<0,(x+4)(x-2)<0 即 -4令 f '(x)=0,解得临界点x=-4,或x=2.
1.求出函数f (x)=x3+3x2-24x-20的单调区间.
复习回顾
解:f '(x)=3x2+6x-24=3(x+4)(x-2).
x (-∞,-4) -4 (-4,2) 2 (2,+∞)
f '(x) 0 0
f (x)
求导数—求临界点—列表—写单调区间
+
+
-
f (x)的单调递减区间为(-4,2).
令 f '(x)=0,解得临界点x=-4,或x=2.
1.求出函数f (x)=x3+3x2-24x-20的单调区间.
复习回顾
f (x)的单调递增区间为(-∞,-4),(2,+∞).
解:f '(x)=3x2+6x-24=3(x+4)(x-2).
x (-∞,-4) -4 (-4,2) 2 (2,+∞)
f '(x) 0 0
f (x)
临界点附近
函数图象有
什么特点?
求导数—求临界点—列表—写单调区间
+
+
-
令 f '(x)=0,解得临界点x=-4,或x=2.
1.求出函数f (x)=x3+3x2-24x-20的单调区间.
复习回顾
f (x)的单调递增区间为(-∞,-4),(2,+∞).
f (x)的单调递减区间为(-4,2).
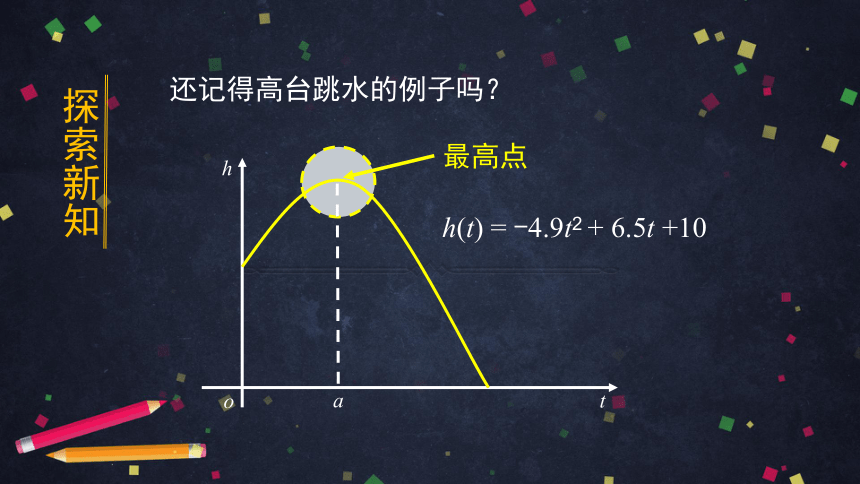
还记得高台跳水的例子吗?
a
t
h
o
最高点
h(t) = -4.9t2 + 6.5t +10
探索新知
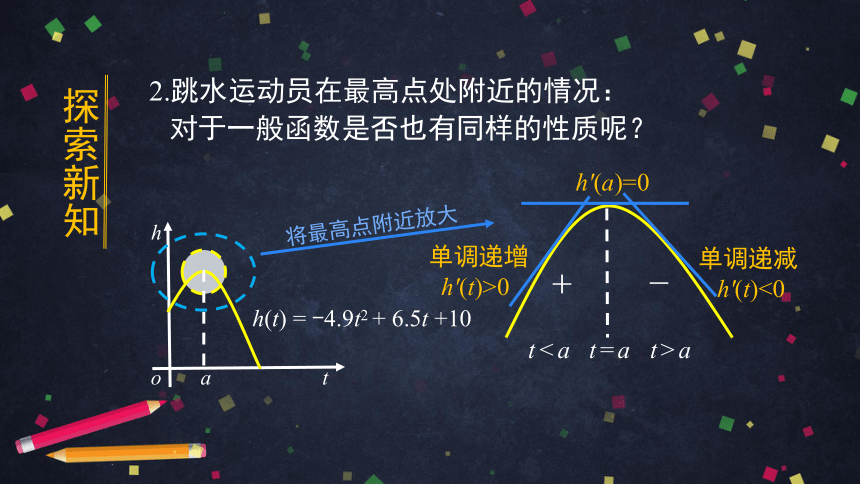
2.跳水运动员在最高点处附近的情况:
(1)当t = a时,运动员距水面高度最大,
h(t)在此点的导数是多少呢?
a
t
h
o
h(t) = -4.9t2 + 6.5t +10
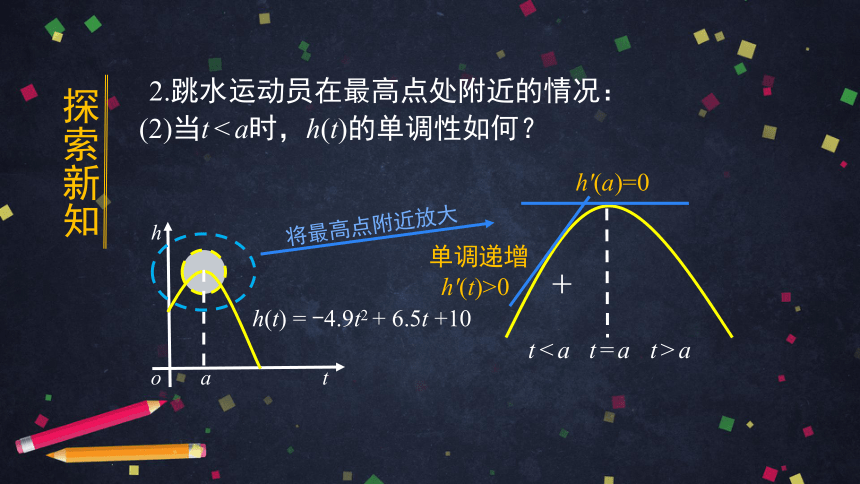
h'(a)=0
探索新知
将最高点附近放大
t = a
t < a
t > a
2.跳水运动员在最高点处附近的情况:
(2)当t < a时,h(t)的单调性如何?
单调递增
h'(t)>0
将最高点附近放大
a
t
h
o
+
h'(a)=0
探索新知
t = a
t < a
t > a
h(t) = -4.9t2 + 6.5t +10
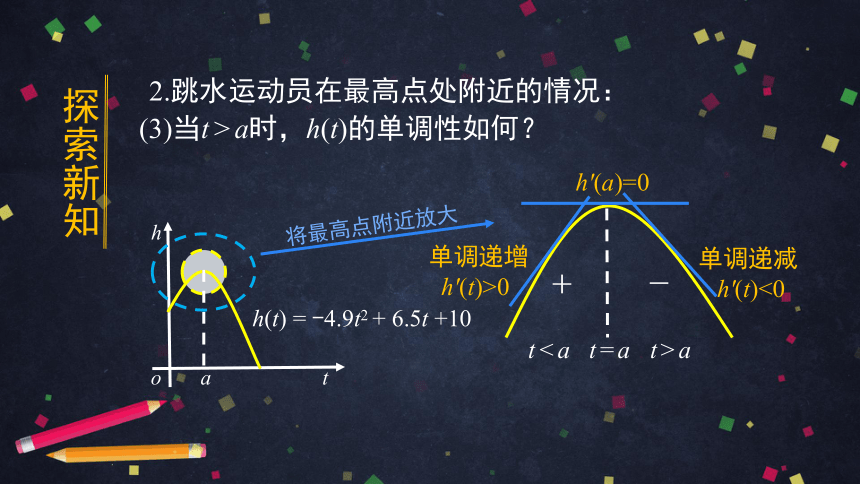
2.跳水运动员在最高点处附近的情况:
单调递减
h'(t)<0
(3)当t > a时,h(t)的单调性如何?
单调递增
h'(t)>0
将最高点附近放大
a
t
h
o
t = a
t < a
t > a
+
-
h'(a)=0
探索新知
h(t) = -4.9t2 + 6.5t +10
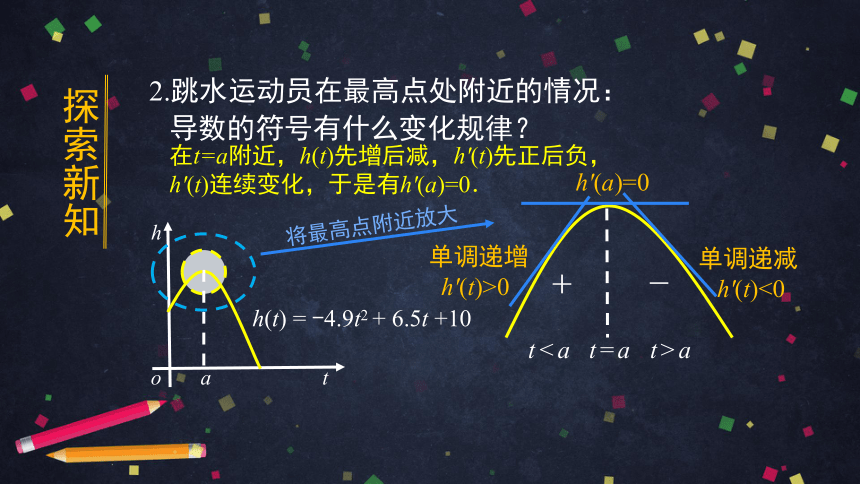
2.跳水运动员在最高点处附近的情况:
导数的符号有什么变化规律?
在t=a附近,h(t)先增后减,h'(t)先正后负,
h'(t)连续变化,于是有h'(a)=0.
单调递减
h'(t)<0
单调递增
h'(t)>0
将最高点附近放大
a
t
h
o
+
-
h'(a)=0
探索新知
t = a
t < a
t > a
h(t) = -4.9t2 + 6.5t +10
2.跳水运动员在最高点处附近的情况:
对于一般函数是否也有同样的性质呢?
单调递减
h'(t)<0
单调递增
h'(t)>0
将最高点附近放大
a
t
h
o
+
-
h'(a)=0
探索新知
t = a
t < a
t > a
h(t) = -4.9t2 + 6.5t +10
3.(1) 如图,函数 y = f (x) 在c,d,e,f,g,h点的函数值与这些点附近的函数值有什么关系?y = f (x) 在这些点的导数值是多少?在这些点附近,y = f (x) 的导数的符号有什么规律?
c d e o f g h x
y
探索新知
y = f (x)
x
y
o
a
b
f '(x)>0
f '(x)>0
f '(x)<0
f '(x)<0
极小值点
极大值点
f '(a)=0
f '(b)=0
3.(2) 如图,函数y=f (x)在a,b点的函数值与这些点附近的函数值有什么关系?y=f (x)在这些点的导数值是多少?在这些点附近,y=f (x)的导数的符号有什么规律?
探索新知
x
y
o
a
b
y=f (x)
x xb
f '(x) + 0 -
f (x) 单调
递增 极大值 单调
递减
f (a)
f (b)
x xa
f '(x) - 0 +
f (x) 单调
递减 极小值 单调
递增
探索新知
一般地,设函数 f (x) 在点 x0 附近有定义, 如果对 x0 附近的所有的点,都有 f (x) < f (x0),我们就说 f (x0) 是 f (x) 的一个极大值,点 x0叫做函数 y = f (x) 的极大值点.
若 f (x) > f (x0),则称 f (x0)是 f (x) 的一个极小值,点 x0 叫做函数 y = f (x) 的极小值点.极小值点、极大值点统称为极值点,极大值和极小值统称为极值.
发现规律
练习 试指出下面函数在[a,b]的极值点与极值,并说出哪些是极大值点,哪些是极小值点.
y
a
b
x1
x2
x3
x4
o
x
f (x4)
f (x3)
f (x1)
f (x2)
发现规律
极大值点:
x1
,x3
极小值点:
x2
,x4
极大值:
f (x1)
,f (x3)
极小值:
f (x2)
,f (x4)
理解极值概念时需注意的几点
深化理解
理解极值概念时需注意的几点
(1)函数的极值是一个局部概念,是仅对某一点的左右两侧附近的点而言的.
深化理解
理解极值概念时需注意的几点
(1)函数的极值是一个局部概念,是仅对某一点的左右两侧附近的点而言的.
(2)极值点是函数定义域内的点,而函数定义域的端点绝不是函数的极值点.
深化理解
理解极值概念时需注意的几点
(1)函数的极值是一个局部概念,是仅对某一点的左右两侧附近的点而言的.
(2)极值点是函数定义域内的点,而函数定义域的端点绝不是函数的极值点.
(3)若f (x)在[a,b]内有极值,那么f (x)在[a,b]内绝不是单调函数,即单调函数在定义域内没有极值.
深化理解
理解极值概念时需注意的几点
(4)极大值与极小值没有必然的大小关系.一个函数在其定义域内可以有许多个极小值和极大值,在某一点的极小值可能大于另一点的极大值(如图(1)).
深化理解
理解极值概念时需注意的几点
(5)若函数f (x)在[a,b]上有极值,它的极值点的分布是有规律的(如图(2)),相邻两个极大值点之间必有一个极小值点,同样相邻两个极小值点之间必有一个极大值点.
深化理解
y
x
o
探究1 极值点处导数值(即切线斜率)有何特点?
结论:极值点处如果有切线,那么切线是水平的,
即 f ?(x)=0.
a
b
y=f (x)
x1
x2
x3
f ?(x1)=0
f ?(x2)=0
f ?(x3)=0
思考 若寻找可导函数的极值点,可否只
由 f '(x) = 0求得即可?
深入探究
分析:x =0是否为函数f (x)=x3的极值点?
f? (x)=3x2 ,当f? (x)=0时,x =0,
而x =0不是该函数的极值点.
x
y
o
f (x) ? x3
探究2 若 f ?(x0)=0,则 x0是否为极值点?
结论:f '(x0)=0是可导函数在x0处取得
极值的必要而不充分条件.
深入探究
f? (x0) =0 x0 是可导函数f (x)的极值点
x0左右两侧导数异号 x0是函数f (x)的极值点 f? (x0)=0
f ?(x)<0
y
x
o
x1
a
b
y=f (x)
极大值点两侧
极小值点两侧
f ?(x)<0
f ?(x)>0
f ?(x)>0
x2
深入探究
探究3 极值点两侧导数正负符号有何规律?
x xx2
f?(x)
f (x)
x xx1
f?(x)
f (x)
增
+
0
-
极大值
减
-
0
增
减
极小值
+
注意:(1)f?(x0)=0时,x0不一定是极值点.
(2)只有f?(x0)=0且x0两侧单调性不同,x0才是极值点.
(3)求极值点,可以先求满足f?(x0) =0的
点x0,再列表判断单调性.
结论:极值点两侧,导数正负符号相异.
探究3 极值点两侧导数正负符号有何规律?
深入探究
例1 求函数 的极值.
学以致用
求导函数f '(x)
求满足f?(x0) =0的x0
判断x0两侧单调性
若x0两侧单调性不同,则f (x0)为极值
分析:
例1 求函数 的极值.
令 f '(x) = 0,解得 x = 2,或 x = -2.
f '(x) > 0,即 x>2,或 x<-2;
f '(x) < 0,即 -2解:因为 ,
所以 f '(x) = x2 - 4 = (x-2)(x+2).
学以致用
例1 求函数 的极值.
当 x 变化时,f '(x), f (x)的变化情况如下表:
x (–∞, –2) –2 (–2, 2) 2 (2, +∞)
f '(x) 0 0
f (x)
–
+
+
单调递增
单调递减
单调递增
所以,当x = –2时,f (x)有极大值 ;
当x = 2时,f (x)有极小值 .
学以致用
例1 求函数 的极值.
令f '(x) = 0,解得x = 2,或 x = -2.
f '(x) > 0,即x>2,或 x<-2;
f '(x) < 0,即-2解:因为 ,
所以f '(x) = x2-4 =(x-2)(x+2).
学以致用
求导整理
求解方程
例1 求函数 的极值.
当 x 变化时,f '(x),f (x)的变化情况如下表:
x (–∞, –2) –2 (–2, 2) 2 ( 2, +∞)
f '(x) 0 0
f (x)
–
+
+
单调递增
单调递减
单调递增
所以,当x = –2时,f (x)有极大值 ;
当x = 2时,f (x)有极小值 .
学以致用
列表断号
求出极值
-2
o
x
y
2
学以致用
例2 求函数f (x)=lnx-x 的极值.
学以致用
求导函数f '(x)
求满足f?(x0) =0的x0
判断x0两侧单调性
若x0两侧单调性不同,则f (x0)为极值
分析:
考虑f (x)的定义域
例2 求函数f (x)=lnx-x 的极值.
解:因为f (x)=lnx-x ,所以
学以致用
x (0, 1) 1 (1, +∞)
f '(x) + 0 -
f (x)
所以,当x=1时,函数有极大值-1;函数无极小值.
极大值
当 x 变化时,f '(x), f (x)的变化情况如下表:
例2 求函数f (x)=lnx-x 的极值.
学以致用
注意:(1)列表时不要忽视定义域;
(2)某些函数可能仅有一个极值.
例3 求函数 的极值.
学以致用
分析:
求f (x)的定义域
求导函数f '(x)
求满足f?(x0) =0的x0
判断x0两侧单调性
若x0两侧单调性不同,则f (x0)为极值
例3 求函数 的极值.
学以致用
x (-∞,-1) -1 (-1,0) (0,1) 1 (1,+∞)
f '(x) + 0 - - 0 +
f (x)
所以,当 x = -1时,函数有极大值-2;
极大值
极小值
例3 求函数 的极值.
当 x 变化时,f '(x), f (x)的变化情况如下表:
导函数的正负是
交替出现的吗?
学以致用
注意:导函数的正负不一定交替出现,
要具体问题具体分析.
当 x = 1时,函数有极小值2.
求函数极值的一般方法:
归纳方法
求函数极值的一般方法:
(1)确定函数的定义域;
归纳方法
求函数极值的一般方法:
(1)确定函数的定义域;
(2)求方程 f '(x) = 0的解;
归纳方法
求函数极值的一般方法:
(1)确定函数的定义域;
(2)求方程 f '(x) = 0的解;
(3)用方程 f '(x) = 0的解,顺次将函数的定义
域分成若干个开区间,并列成表格;
归纳方法
求函数极值的一般方法:
(1)确定函数的定义域;
(2)求方程 f '(x) = 0的解;
(3)用方程 f '(x) = 0的解,顺次将函数的定义
域分成若干个开区间,并列成表格;
(4)由 f '(x) 在方程 f '(x) = 0的解左右的符号来
判断 f (x) 在此处取得极值的情况.
归纳方法
若在x0附近,f '(x) 左正右负,则 f (x0) 为极大值;
+
-
x0
-
+
x0
若在x0附近,f '(x) 左负右正,则 f (x0) 为极小值.
解方程 f '(x) = 0.当 f '(x0) = 0 时:
归纳方法
函数极值
函数极值的定义
函数极值的求法
1.求导;2.求极值点;
3.列表;4.求极值.
函数的性质
单调性
函数的单调性
与导数的关系
用导数研究函数单调性的方法
总结提升
反映函数在某一点
附近的局部性质
1.下图是导函数 y=f '(x) 的图象,试找出函数 y=f (x) 的极值点,并指出哪些是极大值点,哪些是极小值点.
a
b
x
y
x1
o
x2
x3
x4
x5
x6
课后作业
2.求下列函数的极值:
(1) f (x) = 6x2- x- 2 ;
(2) f (x) = x3- 27x ;
(3) f (x) = 6 +12x - x3 ;
(4) f (x) = 3x - x3 .
课后作业
高二年级 数学
函数的极值与导数
函数的性质
单调性
函数的单调性
与导数的关系
用导数研究函数单调性的方法
f '(x)>0,函数单调递增;
f '(x)<0,函数单调递减.
1.求导;2.求临界点;3.列表;4.单调区间.
复习回顾
解:f '(x)=3x2+6x-24=3(x+4)(x-2).
x (-∞,-4) -4 (-4,2) 2 (2,+∞)
f '(x) 0 0
f (x)
+
+
f '(x)>0,(x+4)(x-2)>0 即x<-4或x>2;
令 f '(x)=0,解得临界点x=-4,或x=2.
1.求出函数f (x)=x3+3x2-24x-20的单调区间.
复习回顾
解:f '(x)=3x2+6x-24=3(x+4)(x-2).
x (-∞,-4) -4 (-4,2) 2 (2,+∞)
f '(x) 0 0
f (x)
f (x)的单调递增区间为(-∞,-4),(2,+∞).
+
+
-
f '(x)<0,(x+4)(x-2)<0 即 -4
1.求出函数f (x)=x3+3x2-24x-20的单调区间.
复习回顾
解:f '(x)=3x2+6x-24=3(x+4)(x-2).
x (-∞,-4) -4 (-4,2) 2 (2,+∞)
f '(x) 0 0
f (x)
求导数—求临界点—列表—写单调区间
+
+
-
f (x)的单调递减区间为(-4,2).
令 f '(x)=0,解得临界点x=-4,或x=2.
1.求出函数f (x)=x3+3x2-24x-20的单调区间.
复习回顾
f (x)的单调递增区间为(-∞,-4),(2,+∞).
解:f '(x)=3x2+6x-24=3(x+4)(x-2).
x (-∞,-4) -4 (-4,2) 2 (2,+∞)
f '(x) 0 0
f (x)
临界点附近
函数图象有
什么特点?
求导数—求临界点—列表—写单调区间
+
+
-
令 f '(x)=0,解得临界点x=-4,或x=2.
1.求出函数f (x)=x3+3x2-24x-20的单调区间.
复习回顾
f (x)的单调递增区间为(-∞,-4),(2,+∞).
f (x)的单调递减区间为(-4,2).
还记得高台跳水的例子吗?
a
t
h
o
最高点
h(t) = -4.9t2 + 6.5t +10
探索新知
2.跳水运动员在最高点处附近的情况:
(1)当t = a时,运动员距水面高度最大,
h(t)在此点的导数是多少呢?
a
t
h
o
h(t) = -4.9t2 + 6.5t +10
h'(a)=0
探索新知
将最高点附近放大
t = a
t < a
t > a
2.跳水运动员在最高点处附近的情况:
(2)当t < a时,h(t)的单调性如何?
单调递增
h'(t)>0
将最高点附近放大
a
t
h
o
+
h'(a)=0
探索新知
t = a
t < a
t > a
h(t) = -4.9t2 + 6.5t +10
2.跳水运动员在最高点处附近的情况:
单调递减
h'(t)<0
(3)当t > a时,h(t)的单调性如何?
单调递增
h'(t)>0
将最高点附近放大
a
t
h
o
t = a
t < a
t > a
+
-
h'(a)=0
探索新知
h(t) = -4.9t2 + 6.5t +10
2.跳水运动员在最高点处附近的情况:
导数的符号有什么变化规律?
在t=a附近,h(t)先增后减,h'(t)先正后负,
h'(t)连续变化,于是有h'(a)=0.
单调递减
h'(t)<0
单调递增
h'(t)>0
将最高点附近放大
a
t
h
o
+
-
h'(a)=0
探索新知
t = a
t < a
t > a
h(t) = -4.9t2 + 6.5t +10
2.跳水运动员在最高点处附近的情况:
对于一般函数是否也有同样的性质呢?
单调递减
h'(t)<0
单调递增
h'(t)>0
将最高点附近放大
a
t
h
o
+
-
h'(a)=0
探索新知
t = a
t < a
t > a
h(t) = -4.9t2 + 6.5t +10
3.(1) 如图,函数 y = f (x) 在c,d,e,f,g,h点的函数值与这些点附近的函数值有什么关系?y = f (x) 在这些点的导数值是多少?在这些点附近,y = f (x) 的导数的符号有什么规律?
c d e o f g h x
y
探索新知
y = f (x)
x
y
o
a
b
f '(x)>0
f '(x)>0
f '(x)<0
f '(x)<0
极小值点
极大值点
f '(a)=0
f '(b)=0
3.(2) 如图,函数y=f (x)在a,b点的函数值与这些点附近的函数值有什么关系?y=f (x)在这些点的导数值是多少?在这些点附近,y=f (x)的导数的符号有什么规律?
探索新知
x
y
o
a
b
y=f (x)
x xb
f '(x) + 0 -
f (x) 单调
递增 极大值 单调
递减
f (a)
f (b)
x xa
f '(x) - 0 +
f (x) 单调
递减 极小值 单调
递增
探索新知
一般地,设函数 f (x) 在点 x0 附近有定义, 如果对 x0 附近的所有的点,都有 f (x) < f (x0),我们就说 f (x0) 是 f (x) 的一个极大值,点 x0叫做函数 y = f (x) 的极大值点.
若 f (x) > f (x0),则称 f (x0)是 f (x) 的一个极小值,点 x0 叫做函数 y = f (x) 的极小值点.极小值点、极大值点统称为极值点,极大值和极小值统称为极值.
发现规律
练习 试指出下面函数在[a,b]的极值点与极值,并说出哪些是极大值点,哪些是极小值点.
y
a
b
x1
x2
x3
x4
o
x
f (x4)
f (x3)
f (x1)
f (x2)
发现规律
极大值点:
x1
,x3
极小值点:
x2
,x4
极大值:
f (x1)
,f (x3)
极小值:
f (x2)
,f (x4)
理解极值概念时需注意的几点
深化理解
理解极值概念时需注意的几点
(1)函数的极值是一个局部概念,是仅对某一点的左右两侧附近的点而言的.
深化理解
理解极值概念时需注意的几点
(1)函数的极值是一个局部概念,是仅对某一点的左右两侧附近的点而言的.
(2)极值点是函数定义域内的点,而函数定义域的端点绝不是函数的极值点.
深化理解
理解极值概念时需注意的几点
(1)函数的极值是一个局部概念,是仅对某一点的左右两侧附近的点而言的.
(2)极值点是函数定义域内的点,而函数定义域的端点绝不是函数的极值点.
(3)若f (x)在[a,b]内有极值,那么f (x)在[a,b]内绝不是单调函数,即单调函数在定义域内没有极值.
深化理解
理解极值概念时需注意的几点
(4)极大值与极小值没有必然的大小关系.一个函数在其定义域内可以有许多个极小值和极大值,在某一点的极小值可能大于另一点的极大值(如图(1)).
深化理解
理解极值概念时需注意的几点
(5)若函数f (x)在[a,b]上有极值,它的极值点的分布是有规律的(如图(2)),相邻两个极大值点之间必有一个极小值点,同样相邻两个极小值点之间必有一个极大值点.
深化理解
y
x
o
探究1 极值点处导数值(即切线斜率)有何特点?
结论:极值点处如果有切线,那么切线是水平的,
即 f ?(x)=0.
a
b
y=f (x)
x1
x2
x3
f ?(x1)=0
f ?(x2)=0
f ?(x3)=0
思考 若寻找可导函数的极值点,可否只
由 f '(x) = 0求得即可?
深入探究
分析:x =0是否为函数f (x)=x3的极值点?
f? (x)=3x2 ,当f? (x)=0时,x =0,
而x =0不是该函数的极值点.
x
y
o
f (x) ? x3
探究2 若 f ?(x0)=0,则 x0是否为极值点?
结论:f '(x0)=0是可导函数在x0处取得
极值的必要而不充分条件.
深入探究
f? (x0) =0 x0 是可导函数f (x)的极值点
x0左右两侧导数异号 x0是函数f (x)的极值点 f? (x0)=0
f ?(x)<0
y
x
o
x1
a
b
y=f (x)
极大值点两侧
极小值点两侧
f ?(x)<0
f ?(x)>0
f ?(x)>0
x2
深入探究
探究3 极值点两侧导数正负符号有何规律?
x x
f?(x)
f (x)
x x
f?(x)
f (x)
增
+
0
-
极大值
减
-
0
增
减
极小值
+
注意:(1)f?(x0)=0时,x0不一定是极值点.
(2)只有f?(x0)=0且x0两侧单调性不同,x0才是极值点.
(3)求极值点,可以先求满足f?(x0) =0的
点x0,再列表判断单调性.
结论:极值点两侧,导数正负符号相异.
探究3 极值点两侧导数正负符号有何规律?
深入探究
例1 求函数 的极值.
学以致用
求导函数f '(x)
求满足f?(x0) =0的x0
判断x0两侧单调性
若x0两侧单调性不同,则f (x0)为极值
分析:
例1 求函数 的极值.
令 f '(x) = 0,解得 x = 2,或 x = -2.
f '(x) > 0,即 x>2,或 x<-2;
f '(x) < 0,即 -2
所以 f '(x) = x2 - 4 = (x-2)(x+2).
学以致用
例1 求函数 的极值.
当 x 变化时,f '(x), f (x)的变化情况如下表:
x (–∞, –2) –2 (–2, 2) 2 (2, +∞)
f '(x) 0 0
f (x)
–
+
+
单调递增
单调递减
单调递增
所以,当x = –2时,f (x)有极大值 ;
当x = 2时,f (x)有极小值 .
学以致用
例1 求函数 的极值.
令f '(x) = 0,解得x = 2,或 x = -2.
f '(x) > 0,即x>2,或 x<-2;
f '(x) < 0,即-2
所以f '(x) = x2-4 =(x-2)(x+2).
学以致用
求导整理
求解方程
例1 求函数 的极值.
当 x 变化时,f '(x),f (x)的变化情况如下表:
x (–∞, –2) –2 (–2, 2) 2 ( 2, +∞)
f '(x) 0 0
f (x)
–
+
+
单调递增
单调递减
单调递增
所以,当x = –2时,f (x)有极大值 ;
当x = 2时,f (x)有极小值 .
学以致用
列表断号
求出极值
-2
o
x
y
2
学以致用
例2 求函数f (x)=lnx-x 的极值.
学以致用
求导函数f '(x)
求满足f?(x0) =0的x0
判断x0两侧单调性
若x0两侧单调性不同,则f (x0)为极值
分析:
考虑f (x)的定义域
例2 求函数f (x)=lnx-x 的极值.
解:因为f (x)=lnx-x ,所以
学以致用
x (0, 1) 1 (1, +∞)
f '(x) + 0 -
f (x)
所以,当x=1时,函数有极大值-1;函数无极小值.
极大值
当 x 变化时,f '(x), f (x)的变化情况如下表:
例2 求函数f (x)=lnx-x 的极值.
学以致用
注意:(1)列表时不要忽视定义域;
(2)某些函数可能仅有一个极值.
例3 求函数 的极值.
学以致用
分析:
求f (x)的定义域
求导函数f '(x)
求满足f?(x0) =0的x0
判断x0两侧单调性
若x0两侧单调性不同,则f (x0)为极值
例3 求函数 的极值.
学以致用
x (-∞,-1) -1 (-1,0) (0,1) 1 (1,+∞)
f '(x) + 0 - - 0 +
f (x)
所以,当 x = -1时,函数有极大值-2;
极大值
极小值
例3 求函数 的极值.
当 x 变化时,f '(x), f (x)的变化情况如下表:
导函数的正负是
交替出现的吗?
学以致用
注意:导函数的正负不一定交替出现,
要具体问题具体分析.
当 x = 1时,函数有极小值2.
求函数极值的一般方法:
归纳方法
求函数极值的一般方法:
(1)确定函数的定义域;
归纳方法
求函数极值的一般方法:
(1)确定函数的定义域;
(2)求方程 f '(x) = 0的解;
归纳方法
求函数极值的一般方法:
(1)确定函数的定义域;
(2)求方程 f '(x) = 0的解;
(3)用方程 f '(x) = 0的解,顺次将函数的定义
域分成若干个开区间,并列成表格;
归纳方法
求函数极值的一般方法:
(1)确定函数的定义域;
(2)求方程 f '(x) = 0的解;
(3)用方程 f '(x) = 0的解,顺次将函数的定义
域分成若干个开区间,并列成表格;
(4)由 f '(x) 在方程 f '(x) = 0的解左右的符号来
判断 f (x) 在此处取得极值的情况.
归纳方法
若在x0附近,f '(x) 左正右负,则 f (x0) 为极大值;
+
-
x0
-
+
x0
若在x0附近,f '(x) 左负右正,则 f (x0) 为极小值.
解方程 f '(x) = 0.当 f '(x0) = 0 时:
归纳方法
函数极值
函数极值的定义
函数极值的求法
1.求导;2.求极值点;
3.列表;4.求极值.
函数的性质
单调性
函数的单调性
与导数的关系
用导数研究函数单调性的方法
总结提升
反映函数在某一点
附近的局部性质
1.下图是导函数 y=f '(x) 的图象,试找出函数 y=f (x) 的极值点,并指出哪些是极大值点,哪些是极小值点.
a
b
x
y
x1
o
x2
x3
x4
x5
x6
课后作业
2.求下列函数的极值:
(1) f (x) = 6x2- x- 2 ;
(2) f (x) = x3- 27x ;
(3) f (x) = 6 +12x - x3 ;
(4) f (x) = 3x - x3 .
课后作业
