2019-2020学年高一下学期五一假期作业数学试题(三角函数)(含答案及解析)
文档属性
| 名称 | 2019-2020学年高一下学期五一假期作业数学试题(三角函数)(含答案及解析) |  | |
| 格式 | zip | ||
| 文件大小 | 788.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-06 11:28:05 | ||
图片预览




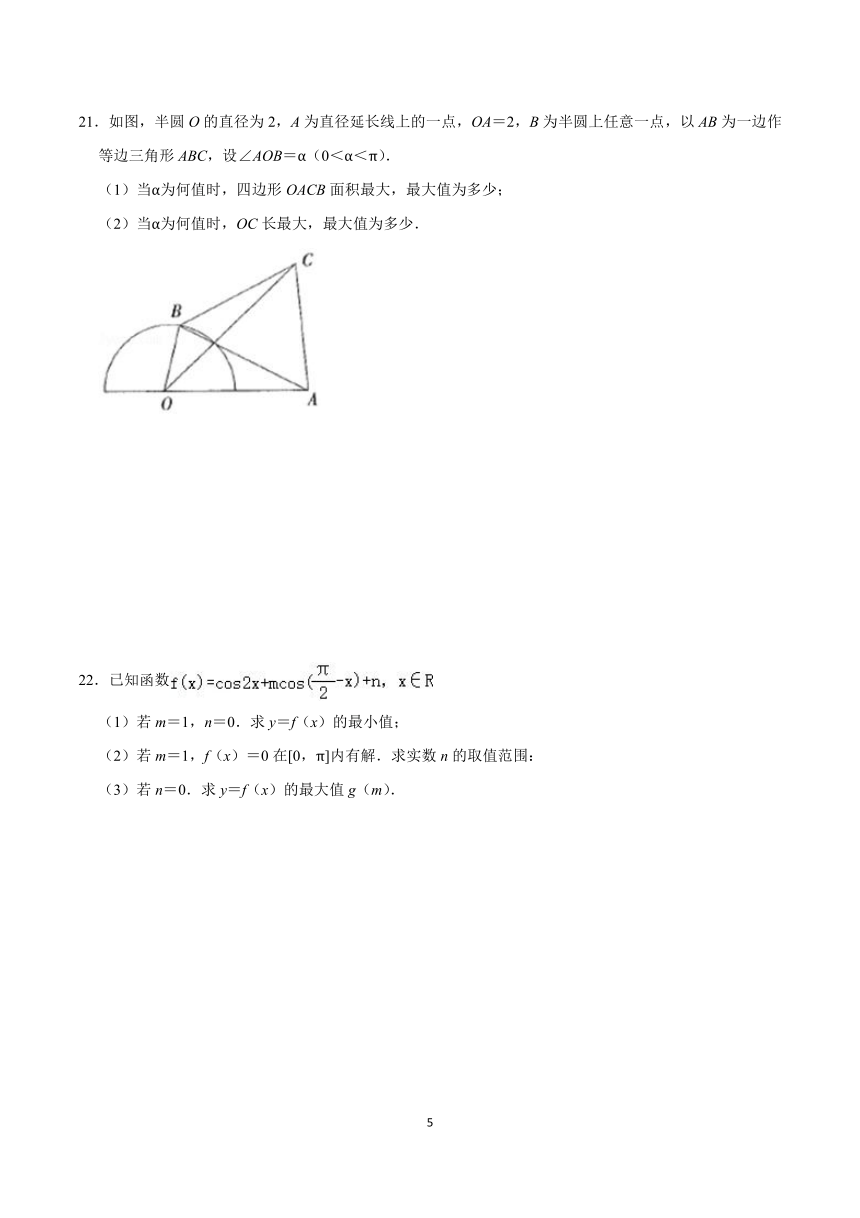
文档简介
1
高一数学阶段性练习(五一假期)
一.选择题(共 8 小题)
1.计算 sin5°cos55°﹣cos175°sin125°的结果是( )
A. B. C. D.
2.若 tanα= ,tan(α+β)= ,则 tanβ=( )
A. B. C. D.
3.若 π≤α≤ π,则 + 等于( )
A.﹣2cos B.2cos C.﹣2sin D.2sin
4.在△ABC中,已知 sinA=2sinBcosC,则该三角形的形状是( )
A.等边三角形 B.直角三角形
C.等腰三角形 D.等腰直角三角形
5.已知 ,那么 的值为( )
A.2 B.﹣2 C. D.2或
6.在△ABC中,AD为 BC边上的中线,E为边 AD的中点,若 ,则 可用 表示为( )
A. B. C. D.
7.在△ABC中,角 A,B,C所对的边分别为 a,b,c下列结论:
①若 a2>b2+c2,则△ABC为钝角三角形;
②若 a2=b2+c2+bc,则 A为 60°;
③若 a2+b2>c2,则△ABC为锐角三角形;
④若 A:B:C=1:2:3,则:a:b:c=1: :2.
其中正确的个数为( )
A.1 B.2 C.3 D.4
8.如图,有一辆汽车在一条水平的公路上向正西行驶,汽车在 A点测得公路北侧山顶 D的仰角为 30°,
汽车行驶 300m后到达 B点测得山顶 D在北偏西 30°方向上,且仰角为 45°,则山的高度 CD为( )
2
A.150 m B.150m C.300 m D.300m
二.多选题(共 4 小题)
9.三角形两边之差为 2,夹角的余弦值为 ,面积为 14,那么,这个三角形的此两边长分别是( )
A.5 B.6 C.7 D.8
10.如图,设△ABC的内角 A,B,C所对的边分别为 a,b,c, ,且 .若
点 D是△ABC外一点,DC=1,DA=3,下列说法中,正确的命题是( )
A.△ABC的内角
B.△ABC的内角
C.四边形 ABCD面积的最大值为
D.四边形 ABCD面积无最大值
11.在△ABC中,角 A,B,C所对的边分别为 a,b,c,且(a+b):(a+c):(b+c)=9:10:11,则下
列结论正确的是( )
A.sinA:sinB:sinC=4:5:6
B.△ABC是钝角三角形
C.△ABC的最大内角是最小内角的 2倍
D.若 c=6,则△ABC外接圆半径为
3
12.已知△ABC的内角 A,B,C所对的边分别为 a,b,c,下列四个命题中正确的命题是( )
A.若 ,则△ABC一定是等边三角形
B.若 acosA=bcosB,则△ABC一定是等腰三角形
C.若 bcosC+ccosB=b,则△ABC一定是等腰三角形
D.若 a2+b2﹣c2>0,则△ABC一定是锐角三角形
三.填空题(共 4 小题)
13.函数 f(x)=asin(x+ )+3sin(x﹣ )是偶函数,则 a= ,f(x)的最大值是 .
14.若 ,其中θ∈[0,π],则 |的最大值为 .
15. = .
16.已知△ABC,若存在△A1B1C1,满足 ,则称△A1B1C1是△ABC的一个“对
偶”三角形,若等腰△ABC存在“对偶”三角形,则其底角的弧度数为 .
四.解答题(共 6 小题)
17.如图,在△ABC中,已知点 D在 BC边上,AD⊥AC, ,AD=3,△ABD的面积为 .
(1)求 sin∠BAC的值;
(2)求 BD的长.
4
18.在△ABC中,角 A,B,C所对的边分别是 a,b,c.已知 .
(1)求 b的值;
(2)求△ABC的面积.
19.已知函数
(1)当 m=0时,求 f(x)在区间 上的取值范围;
(2)当 tanα=2时, ,求 m的值.
20.已知函数 在 R 上的最大值为 3
(1)求 m的值及函数 f(x)的单调递增区间
(2)若锐角△ABC中角 A、B,C所对的边分别为 a、b、c,且 f(A)=0,求 的取值范围
5
21.如图,半圆 O的直径为 2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以 AB为一边作
等边三角形 ABC,设∠AOB=α(0<α<π).
(1)当α为何值时,四边形 OACB面积最大,最大值为多少;
(2)当α为何值时,OC长最大,最大值为多少.
22.已知函数
(1)若 m=1,n=0.求 y=f(x)的最小值;
(2)若 m=1,f(x)=0在[0,π]内有解.求实数 n的取值范围:
(3)若 n=0.求 y=f(x)的最大值 g(m).
6
试题解析
一.选择题(共 8 小题)
1.计算 sin5°cos55°﹣cos175°sin125°的结果是( )
A. B. C. D.
【解答】sin5°cos55°﹣cos175°sin125°
=sin5°cos55°+cos5°sin55°
=sin60°
= .
故选:D.
2.若 tanα= ,tan(α+β)= ,则 tanβ=( )
A. B. C. D.
【解答】∵tanα= ,tan(α+β)= ,则 tanβ=tan[(α+β)﹣α]= =
= ,
故选:A.
3.若 π≤α≤ π,则 + 等于( )
A.﹣2cos B.2cos C.﹣2sin D.2sin
【解答】∵ π≤α≤ π,∴ ∈[ , ],∴sin ≤cos <0,
则 + = +
=|cos +sin |+|cos ﹣sin |=﹣cos ﹣sin +cos ﹣sin =﹣2sin ,
故选:C.
4.在△ABC中,已知 sinA=2sinBcosC,则该三角形的形状是( )
A.等边三角形 B.直角三角形
C.等腰三角形 D.等腰直角三角形
7
【解答】因为 sinA=2sinBcosc,所以 sin(B+C)=2sinBcosC,
所以 sinBcosC﹣sinCcosB=0,即 sin(B﹣C)=0,
因为 A,B,C是三角形内角,所以 B=C.
所以三角形是等腰三角形.
故选:C.
5.已知 ,那么 的值为( )
A.2 B.﹣2 C. D.2或
【解答】∵sin2 +cos2 =1
∴ = = =﹣
解得 tan =2或
故选:D.
6.在△ABC中,AD为 BC边上的中线,E为边 AD的中点,若 ,则 可用 表示为( )
A. B. C. D.
【解答】由题意可得, = = ,
则 = = = .
故选:B.
7.在△ABC中,角 A,B,C所对的边分别为 a,b,c下列结论:
①若 a2>b2+c2,则△ABC为钝角三角形;
②若 a2=b2+c2+bc,则 A为 60°;
③若 a2+b2>c2,则△ABC为锐角三角形;
④若 A:B:C=1:2:3,则:a:b:c=1: :2.
其中正确的个数为( )
A.1 B.2 C.3 D.4
【解答】①若 a2>b2+c2,则 cosA= <0,则角 A是钝角,则△ABC为钝角三角形,故①正
确,
8
②若 a2=b2+c2+bc,则 b2+c2﹣a2=﹣bc,则 cosA= = ,则 A为 120°,故②错
误,
③若 a2+b2>c2,则 cosC= >0,则角 C是锐角,无法判断角 A,B的取值,故△ABC为锐
角三角形不正确,故③错误;
④若 A:B:C=1:2:3,则 A=30°,B=60°,C=90°,
则 a:b:c=sinA:sinB:sinC= : :1=1: :2,故④正确,
故正确是①④,
故选:B.
8.如图,有一辆汽车在一条水平的公路上向正西行驶,汽车在 A点测得公路北侧山顶 D的仰角为 30°,
汽车行驶 300m后到达 B点测得山顶 D在北偏西 30°方向上,且仰角为 45°,则山的高度 CD为( )
A.150 m B.150m C.300 m D.300m
【解答】由题意可得在直角三角形 DCA中,∠DAC=30°,DC⊥AC,
设 CD=h,可得 AC=htan60°= h,
在直角三角形 DCB中,∠DBC=45°,DC⊥BC,
可得 CB=htan45°=h,
又∠CBA=120°,可得 AC2=AB2+CB2﹣2AB?CB?cos120°,
即为 3h2=3002+h2+300h,
解得 h=300(负的舍去).
故选:D.
9.三角形两边之差为 2,夹角的余弦值为 ,面积为 14,那么,这个三角形的此两边长分别是( )
A.3和 5 B.4和 6 C.6和 8 D.5和 7
【解答】如图所示,
9
假设已知 a﹣c=2, ,S△ABC=14.
∵0<B<π,∴ = .
又 14= ,∴ac=35.
联立 ,∵a,c>0,解得
∴这个三角形的此两边长分别是 5和 7.
故选:D.
二.多选题(共 4 小题)
10.如图,设△ABC的内角 A,B,C所对的边分别为 a,b,c, ,且 .若
点 D是△ABC外一点,DC=1,DA=3,下列说法中,正确的命题是( )
A.△ABC的内角
B.△ABC的内角
C.四边形 ABCD面积的最大值为
D.四边形 ABCD面积无最大值
【解答】∵ ,
∴ (sinAcosC+sinCcosA)=2sinB?sinB,
∴sinB= ,
∴B= .故 A正确.
又∵ .
∴C= ,故 B正确.
等边△ABC中,设 AC=x,x>0,
在△ADC中,由余弦定理可得:AC2=AD2+CD2﹣2AD?CD?cosD,
10
由于 AD=3,DC=1,代入上式可得:x2=10﹣6cosD
∴S 四边形 ABCD=S△ABC+S△ACD= + = + = +
=3sin(D﹣ )+ ,
∴四边形 ABCD面积的最大值为 ,故 C正确.
故选:ABC.
11.在△ABC中,角 A,B,C所对的边分别为 a,b,c,且(a+b):(a+c):(b+c)=9:10:11,则下
列结论正确的是( )
A.sinA:sinB:sinC=4:5:6
B.△ABC是钝角三角形
C.△ABC的最大内角是最小内角的 2倍
D.若 c=6,则△ABC外接圆半径为
【解答】(a+b):(a+c):(b+c)=9:10:11,可设 a+b=9t,a+c=10t,b+c=11t,
解得 a=4t,b=5t,c=6t,t>0,
可得 sinA:sinB:sinC=a:b:c=4:5:6,故 A正确;
由 c为最大边,可得 cosC= = = >0,即 C为锐角,故 B错误;
由 cosA= = = ,由 cos2A=2cos2A﹣1=2× ﹣1= =cosC,
由 2A,C∈(0,π),可得 2A=C,故 C正确;
若 c=6,可得 2R= = = ,△ABC外接圆半径为 ,故 D正确.
故选:ACD.
12.已知△ABC的内角 A,B,C所对的边分别为 a,b,c,下列四个命题中正确的命题是( )
A.若 ,则△ABC一定是等边三角形
B.若 acosA=bcosB,则△ABC一定是等腰三角形
C.若 bcosC+ccosB=b,则△ABC一定是等腰三角形
D.若 a2+b2﹣c2>0,则△ABC一定是锐角三角形
【解答】对于 A,若 ,则 ,即 tanA=tanB=tanC,即 A=B=
C,即△ABC是等边三角形,故正确;
11
对于 B,若 acosA=bcosB,则由正弦定理得 2rsinAcosA=2rsinBcosB,即 sin2A=sin2B,则 2A=2B或 2A+2B
=180,即 A=B或 A+B=90°,则△ABC为等腰三角形或直角三角形,故错误;
对于 C,若 bcosC+ccosB=b,sinBcosC+sinCcosB=sin(B+C)=sinA=sinB,即 A=B,则△ABC是等
腰三角形,故正确;
对于 D,△ABC中,∵a2+b2﹣c2>0,∴角 C为锐角,但△ABC不一定是锐角三角形,故错误;
故选:AC.
三.填空题(共 4 小题)
13.函数 f(x)=asin(x+ )+3sin(x﹣ )是偶函数,则 a= ﹣3 ,f(x)的最大值是 3 .
【解答】∵函数 f(x)=asin(x+ )+3sin(x﹣ )是偶函数,则 f(﹣x)=f(x),
即 asin(﹣x+ )+3sin(﹣x﹣ )=[asin(x+ )+3sin(x﹣ )],
即﹣asinxcos +acosxsin ﹣3(sinxcos +cosxsin )=asinxcos +acosxsin +3(sinxcos ﹣
cosxsin ).
求得 a=﹣3.
故 f(x)=﹣3sin(x+ )+3sin(x﹣ )=﹣3(sinxcos +cosxsin )+3(sinxcos ﹣cosxsin )
=﹣6cosxsin =﹣3 cosx,
故函数 f(x)的最大值为 3 .
14.若 ,其中θ∈[0,π],则 |的最大值为 3 .
【解答】 ,
所以 θ+4sinθ+2,
因为θ∈[0,π],令 t=sinθ∈[0,1],
所以 +4t+2=3( )2+ ,
所以当 t=1时,取最大值 9,
所以 |的最大值为 3,
故答案为:3.
15. = 8 .
12
【解答】原式= = = = =
8. 故答案为:8
16.已知△ABC,若存在△A1B1C1,满足 ,则称△A1B1C1是△ABC的一个“对
偶”三角形,若等腰△ABC存在“对偶”三角形,则其底角的弧度数为 .
【解答】设 A=B,由已知得 sinA1=sinB1,cosA=sinA1,cosB=sinB1,cosC=sinC1,则 A1=B1,
所以 A+A1= ,B+B1= ,C+C1= (舍)或 A+A1= ,B+B1= ,C=C1﹣ ,
解得 C= ,A=B= = .
故答案是: .
四.解答题(共 6 小题)
17.如图,在△ABC中,已知点 D在 BC边上,AD⊥AC, ,AD=3,△ABD的面积为 .
(1)求 sin∠BAC的值;
(2)求 BD的长.
【解答】(1)△ABD的面积为
解得 ,
又易知∠BAD为锐角,所以 ,
所以 .
(2)根据余弦定理可得:cos∠BAD= ,
∴ = , ∴解得 BD= .
18.在△ABC中,角 A,B,C所对的边分别是 a,b,c.已知 .
13
(1)求 b的值;
(2)求△ABC的面积.
【解答】(1)∵cosA= ,A∈(0,π),∴sinA= = ,
∴sinB=sin(A+ )=cosA= .
由正弦定理可得:b= = =3 .
(2)由 B=A+ ,可知:B为钝角.
A,C为锐角.
由余弦定理可得:a2=b2+c2﹣2bccosA,
∴32= +c2﹣2× c× ,
化为:c2﹣4 c+9=0,c<b.
解得 c= .
∴△ABC的面积 S= = = .
19.已知函数
(1)当 m=0时,求 f(x)在区间 上的取值范围;
(2)当 tanα=2时, ,求 m的值.
【解答】(1)当 m=0时,f(x)=f(x)=sin2x+sinxcosx= +
=
由于
所以:
f(x)
(2)由于
14
=
所以:f(α)=
tanα=2
所以: ,cos2α=
由于:
解得:m=﹣4
20.已知函数 在 R 上的最大值为 3
(1)求 m的值及函数 f(x)的单调递增区间
(2)若锐角△ABC中角 A、B,C所对的边分别为 a、b、c,且 f(A)=0,求 的取值范围
【解答】(1)
= = ,
由已知 2+m=3,∴m=1,
因此 ,
令 ,得 ,
因此函数 f(x)的单调递增区间为
(2)由已知 ,∴ ,
由 得 ,
因此 ∴ ,
∴ ,
∵为锐角三角形△ABC,∴ ,解得 ,
15
因此 ,那么 ,
∴求 的取值范围为 .
21.如图,半圆 O的直径为 2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以 AB为一边作
等边三角形 ABC,设∠AOB=α(0<α<π).
(1)当α为何值时,四边形 OACB面积最大,最大值为多少;
(2)当α为何值时,OC长最大,最大值为多少.
【解答】(1)由题意,在△OAB中,AB2=5﹣4cosα,
三角形 S△AOB=sinα,
三角形
四边形 OABC的面积为 .
∵0<α<π,
∴当 ,即 时,四边形 OABC的面积最大,
故得当 ,四边形 OABC的面积最大且最大值为 .
(2)△OAB中,
∴
∴ .
△OAC中,OC2=OA2+AC2﹣2OA?AC?cos∠OAC=
即
∵ ,
∴ ,即 时,OC有最大值.
16
故得当 时,OC有最大值 3.
22.已知函数
(1)若 m=1,n=0.求 y=f(x)的最小值;
(2)若 m=1,f(x)=0在[0,π]内有解.求实数 n的取值范围:
(3)若 n=0.求 y=f(x)的最大值 g(m).
【解答】(1)对于函数 f(x)=cos2x+mcos( ﹣x)+n=cos2x+msinx+n,
若 m=1,n=0,则函数 f(x)=cos2x+sinx,
当 ,k∈Z 时,cos2x和 sinx 同时取得最小值﹣1,
故 f(x)取得最小值为﹣2;
(2)若 m=1,f(x)=cos2x+sinx+n=0在[0,π]内有解,
故直线 y=n和曲线 y=﹣cos2x﹣sinx在[0,π]内有交点,
由 y=﹣cos2x﹣sinx=2sin2x﹣sinx﹣1,
令 sinx=t,t∈[0,1],则 y=2t2﹣t﹣1∈ ,
∴实数 n的取值范围是 ;
(3)若 n=0,则 f(x)=cos2x+msinx=﹣2sin2x+msinx+1,
令 sinx=t,t∈[﹣1,1],
则 y=﹣2t2+mt+1,对称轴方程为 t= .
当 <﹣1,即 m<﹣4时,g(m)=﹣m﹣1;
当﹣1 ,即﹣4≤m≤4,g(m)= ;
当 >1,即 m>4时,g(m)=m﹣1.
综上,g(m)=
高一数学阶段性练习(五一假期)
一.选择题(共 8 小题)
1.计算 sin5°cos55°﹣cos175°sin125°的结果是( )
A. B. C. D.
2.若 tanα= ,tan(α+β)= ,则 tanβ=( )
A. B. C. D.
3.若 π≤α≤ π,则 + 等于( )
A.﹣2cos B.2cos C.﹣2sin D.2sin
4.在△ABC中,已知 sinA=2sinBcosC,则该三角形的形状是( )
A.等边三角形 B.直角三角形
C.等腰三角形 D.等腰直角三角形
5.已知 ,那么 的值为( )
A.2 B.﹣2 C. D.2或
6.在△ABC中,AD为 BC边上的中线,E为边 AD的中点,若 ,则 可用 表示为( )
A. B. C. D.
7.在△ABC中,角 A,B,C所对的边分别为 a,b,c下列结论:
①若 a2>b2+c2,则△ABC为钝角三角形;
②若 a2=b2+c2+bc,则 A为 60°;
③若 a2+b2>c2,则△ABC为锐角三角形;
④若 A:B:C=1:2:3,则:a:b:c=1: :2.
其中正确的个数为( )
A.1 B.2 C.3 D.4
8.如图,有一辆汽车在一条水平的公路上向正西行驶,汽车在 A点测得公路北侧山顶 D的仰角为 30°,
汽车行驶 300m后到达 B点测得山顶 D在北偏西 30°方向上,且仰角为 45°,则山的高度 CD为( )
2
A.150 m B.150m C.300 m D.300m
二.多选题(共 4 小题)
9.三角形两边之差为 2,夹角的余弦值为 ,面积为 14,那么,这个三角形的此两边长分别是( )
A.5 B.6 C.7 D.8
10.如图,设△ABC的内角 A,B,C所对的边分别为 a,b,c, ,且 .若
点 D是△ABC外一点,DC=1,DA=3,下列说法中,正确的命题是( )
A.△ABC的内角
B.△ABC的内角
C.四边形 ABCD面积的最大值为
D.四边形 ABCD面积无最大值
11.在△ABC中,角 A,B,C所对的边分别为 a,b,c,且(a+b):(a+c):(b+c)=9:10:11,则下
列结论正确的是( )
A.sinA:sinB:sinC=4:5:6
B.△ABC是钝角三角形
C.△ABC的最大内角是最小内角的 2倍
D.若 c=6,则△ABC外接圆半径为
3
12.已知△ABC的内角 A,B,C所对的边分别为 a,b,c,下列四个命题中正确的命题是( )
A.若 ,则△ABC一定是等边三角形
B.若 acosA=bcosB,则△ABC一定是等腰三角形
C.若 bcosC+ccosB=b,则△ABC一定是等腰三角形
D.若 a2+b2﹣c2>0,则△ABC一定是锐角三角形
三.填空题(共 4 小题)
13.函数 f(x)=asin(x+ )+3sin(x﹣ )是偶函数,则 a= ,f(x)的最大值是 .
14.若 ,其中θ∈[0,π],则 |的最大值为 .
15. = .
16.已知△ABC,若存在△A1B1C1,满足 ,则称△A1B1C1是△ABC的一个“对
偶”三角形,若等腰△ABC存在“对偶”三角形,则其底角的弧度数为 .
四.解答题(共 6 小题)
17.如图,在△ABC中,已知点 D在 BC边上,AD⊥AC, ,AD=3,△ABD的面积为 .
(1)求 sin∠BAC的值;
(2)求 BD的长.
4
18.在△ABC中,角 A,B,C所对的边分别是 a,b,c.已知 .
(1)求 b的值;
(2)求△ABC的面积.
19.已知函数
(1)当 m=0时,求 f(x)在区间 上的取值范围;
(2)当 tanα=2时, ,求 m的值.
20.已知函数 在 R 上的最大值为 3
(1)求 m的值及函数 f(x)的单调递增区间
(2)若锐角△ABC中角 A、B,C所对的边分别为 a、b、c,且 f(A)=0,求 的取值范围
5
21.如图,半圆 O的直径为 2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以 AB为一边作
等边三角形 ABC,设∠AOB=α(0<α<π).
(1)当α为何值时,四边形 OACB面积最大,最大值为多少;
(2)当α为何值时,OC长最大,最大值为多少.
22.已知函数
(1)若 m=1,n=0.求 y=f(x)的最小值;
(2)若 m=1,f(x)=0在[0,π]内有解.求实数 n的取值范围:
(3)若 n=0.求 y=f(x)的最大值 g(m).
6
试题解析
一.选择题(共 8 小题)
1.计算 sin5°cos55°﹣cos175°sin125°的结果是( )
A. B. C. D.
【解答】sin5°cos55°﹣cos175°sin125°
=sin5°cos55°+cos5°sin55°
=sin60°
= .
故选:D.
2.若 tanα= ,tan(α+β)= ,则 tanβ=( )
A. B. C. D.
【解答】∵tanα= ,tan(α+β)= ,则 tanβ=tan[(α+β)﹣α]= =
= ,
故选:A.
3.若 π≤α≤ π,则 + 等于( )
A.﹣2cos B.2cos C.﹣2sin D.2sin
【解答】∵ π≤α≤ π,∴ ∈[ , ],∴sin ≤cos <0,
则 + = +
=|cos +sin |+|cos ﹣sin |=﹣cos ﹣sin +cos ﹣sin =﹣2sin ,
故选:C.
4.在△ABC中,已知 sinA=2sinBcosC,则该三角形的形状是( )
A.等边三角形 B.直角三角形
C.等腰三角形 D.等腰直角三角形
7
【解答】因为 sinA=2sinBcosc,所以 sin(B+C)=2sinBcosC,
所以 sinBcosC﹣sinCcosB=0,即 sin(B﹣C)=0,
因为 A,B,C是三角形内角,所以 B=C.
所以三角形是等腰三角形.
故选:C.
5.已知 ,那么 的值为( )
A.2 B.﹣2 C. D.2或
【解答】∵sin2 +cos2 =1
∴ = = =﹣
解得 tan =2或
故选:D.
6.在△ABC中,AD为 BC边上的中线,E为边 AD的中点,若 ,则 可用 表示为( )
A. B. C. D.
【解答】由题意可得, = = ,
则 = = = .
故选:B.
7.在△ABC中,角 A,B,C所对的边分别为 a,b,c下列结论:
①若 a2>b2+c2,则△ABC为钝角三角形;
②若 a2=b2+c2+bc,则 A为 60°;
③若 a2+b2>c2,则△ABC为锐角三角形;
④若 A:B:C=1:2:3,则:a:b:c=1: :2.
其中正确的个数为( )
A.1 B.2 C.3 D.4
【解答】①若 a2>b2+c2,则 cosA= <0,则角 A是钝角,则△ABC为钝角三角形,故①正
确,
8
②若 a2=b2+c2+bc,则 b2+c2﹣a2=﹣bc,则 cosA= = ,则 A为 120°,故②错
误,
③若 a2+b2>c2,则 cosC= >0,则角 C是锐角,无法判断角 A,B的取值,故△ABC为锐
角三角形不正确,故③错误;
④若 A:B:C=1:2:3,则 A=30°,B=60°,C=90°,
则 a:b:c=sinA:sinB:sinC= : :1=1: :2,故④正确,
故正确是①④,
故选:B.
8.如图,有一辆汽车在一条水平的公路上向正西行驶,汽车在 A点测得公路北侧山顶 D的仰角为 30°,
汽车行驶 300m后到达 B点测得山顶 D在北偏西 30°方向上,且仰角为 45°,则山的高度 CD为( )
A.150 m B.150m C.300 m D.300m
【解答】由题意可得在直角三角形 DCA中,∠DAC=30°,DC⊥AC,
设 CD=h,可得 AC=htan60°= h,
在直角三角形 DCB中,∠DBC=45°,DC⊥BC,
可得 CB=htan45°=h,
又∠CBA=120°,可得 AC2=AB2+CB2﹣2AB?CB?cos120°,
即为 3h2=3002+h2+300h,
解得 h=300(负的舍去).
故选:D.
9.三角形两边之差为 2,夹角的余弦值为 ,面积为 14,那么,这个三角形的此两边长分别是( )
A.3和 5 B.4和 6 C.6和 8 D.5和 7
【解答】如图所示,
9
假设已知 a﹣c=2, ,S△ABC=14.
∵0<B<π,∴ = .
又 14= ,∴ac=35.
联立 ,∵a,c>0,解得
∴这个三角形的此两边长分别是 5和 7.
故选:D.
二.多选题(共 4 小题)
10.如图,设△ABC的内角 A,B,C所对的边分别为 a,b,c, ,且 .若
点 D是△ABC外一点,DC=1,DA=3,下列说法中,正确的命题是( )
A.△ABC的内角
B.△ABC的内角
C.四边形 ABCD面积的最大值为
D.四边形 ABCD面积无最大值
【解答】∵ ,
∴ (sinAcosC+sinCcosA)=2sinB?sinB,
∴sinB= ,
∴B= .故 A正确.
又∵ .
∴C= ,故 B正确.
等边△ABC中,设 AC=x,x>0,
在△ADC中,由余弦定理可得:AC2=AD2+CD2﹣2AD?CD?cosD,
10
由于 AD=3,DC=1,代入上式可得:x2=10﹣6cosD
∴S 四边形 ABCD=S△ABC+S△ACD= + = + = +
=3sin(D﹣ )+ ,
∴四边形 ABCD面积的最大值为 ,故 C正确.
故选:ABC.
11.在△ABC中,角 A,B,C所对的边分别为 a,b,c,且(a+b):(a+c):(b+c)=9:10:11,则下
列结论正确的是( )
A.sinA:sinB:sinC=4:5:6
B.△ABC是钝角三角形
C.△ABC的最大内角是最小内角的 2倍
D.若 c=6,则△ABC外接圆半径为
【解答】(a+b):(a+c):(b+c)=9:10:11,可设 a+b=9t,a+c=10t,b+c=11t,
解得 a=4t,b=5t,c=6t,t>0,
可得 sinA:sinB:sinC=a:b:c=4:5:6,故 A正确;
由 c为最大边,可得 cosC= = = >0,即 C为锐角,故 B错误;
由 cosA= = = ,由 cos2A=2cos2A﹣1=2× ﹣1= =cosC,
由 2A,C∈(0,π),可得 2A=C,故 C正确;
若 c=6,可得 2R= = = ,△ABC外接圆半径为 ,故 D正确.
故选:ACD.
12.已知△ABC的内角 A,B,C所对的边分别为 a,b,c,下列四个命题中正确的命题是( )
A.若 ,则△ABC一定是等边三角形
B.若 acosA=bcosB,则△ABC一定是等腰三角形
C.若 bcosC+ccosB=b,则△ABC一定是等腰三角形
D.若 a2+b2﹣c2>0,则△ABC一定是锐角三角形
【解答】对于 A,若 ,则 ,即 tanA=tanB=tanC,即 A=B=
C,即△ABC是等边三角形,故正确;
11
对于 B,若 acosA=bcosB,则由正弦定理得 2rsinAcosA=2rsinBcosB,即 sin2A=sin2B,则 2A=2B或 2A+2B
=180,即 A=B或 A+B=90°,则△ABC为等腰三角形或直角三角形,故错误;
对于 C,若 bcosC+ccosB=b,sinBcosC+sinCcosB=sin(B+C)=sinA=sinB,即 A=B,则△ABC是等
腰三角形,故正确;
对于 D,△ABC中,∵a2+b2﹣c2>0,∴角 C为锐角,但△ABC不一定是锐角三角形,故错误;
故选:AC.
三.填空题(共 4 小题)
13.函数 f(x)=asin(x+ )+3sin(x﹣ )是偶函数,则 a= ﹣3 ,f(x)的最大值是 3 .
【解答】∵函数 f(x)=asin(x+ )+3sin(x﹣ )是偶函数,则 f(﹣x)=f(x),
即 asin(﹣x+ )+3sin(﹣x﹣ )=[asin(x+ )+3sin(x﹣ )],
即﹣asinxcos +acosxsin ﹣3(sinxcos +cosxsin )=asinxcos +acosxsin +3(sinxcos ﹣
cosxsin ).
求得 a=﹣3.
故 f(x)=﹣3sin(x+ )+3sin(x﹣ )=﹣3(sinxcos +cosxsin )+3(sinxcos ﹣cosxsin )
=﹣6cosxsin =﹣3 cosx,
故函数 f(x)的最大值为 3 .
14.若 ,其中θ∈[0,π],则 |的最大值为 3 .
【解答】 ,
所以 θ+4sinθ+2,
因为θ∈[0,π],令 t=sinθ∈[0,1],
所以 +4t+2=3( )2+ ,
所以当 t=1时,取最大值 9,
所以 |的最大值为 3,
故答案为:3.
15. = 8 .
12
【解答】原式= = = = =
8. 故答案为:8
16.已知△ABC,若存在△A1B1C1,满足 ,则称△A1B1C1是△ABC的一个“对
偶”三角形,若等腰△ABC存在“对偶”三角形,则其底角的弧度数为 .
【解答】设 A=B,由已知得 sinA1=sinB1,cosA=sinA1,cosB=sinB1,cosC=sinC1,则 A1=B1,
所以 A+A1= ,B+B1= ,C+C1= (舍)或 A+A1= ,B+B1= ,C=C1﹣ ,
解得 C= ,A=B= = .
故答案是: .
四.解答题(共 6 小题)
17.如图,在△ABC中,已知点 D在 BC边上,AD⊥AC, ,AD=3,△ABD的面积为 .
(1)求 sin∠BAC的值;
(2)求 BD的长.
【解答】(1)△ABD的面积为
解得 ,
又易知∠BAD为锐角,所以 ,
所以 .
(2)根据余弦定理可得:cos∠BAD= ,
∴ = , ∴解得 BD= .
18.在△ABC中,角 A,B,C所对的边分别是 a,b,c.已知 .
13
(1)求 b的值;
(2)求△ABC的面积.
【解答】(1)∵cosA= ,A∈(0,π),∴sinA= = ,
∴sinB=sin(A+ )=cosA= .
由正弦定理可得:b= = =3 .
(2)由 B=A+ ,可知:B为钝角.
A,C为锐角.
由余弦定理可得:a2=b2+c2﹣2bccosA,
∴32= +c2﹣2× c× ,
化为:c2﹣4 c+9=0,c<b.
解得 c= .
∴△ABC的面积 S= = = .
19.已知函数
(1)当 m=0时,求 f(x)在区间 上的取值范围;
(2)当 tanα=2时, ,求 m的值.
【解答】(1)当 m=0时,f(x)=f(x)=sin2x+sinxcosx= +
=
由于
所以:
f(x)
(2)由于
14
=
所以:f(α)=
tanα=2
所以: ,cos2α=
由于:
解得:m=﹣4
20.已知函数 在 R 上的最大值为 3
(1)求 m的值及函数 f(x)的单调递增区间
(2)若锐角△ABC中角 A、B,C所对的边分别为 a、b、c,且 f(A)=0,求 的取值范围
【解答】(1)
= = ,
由已知 2+m=3,∴m=1,
因此 ,
令 ,得 ,
因此函数 f(x)的单调递增区间为
(2)由已知 ,∴ ,
由 得 ,
因此 ∴ ,
∴ ,
∵为锐角三角形△ABC,∴ ,解得 ,
15
因此 ,那么 ,
∴求 的取值范围为 .
21.如图,半圆 O的直径为 2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以 AB为一边作
等边三角形 ABC,设∠AOB=α(0<α<π).
(1)当α为何值时,四边形 OACB面积最大,最大值为多少;
(2)当α为何值时,OC长最大,最大值为多少.
【解答】(1)由题意,在△OAB中,AB2=5﹣4cosα,
三角形 S△AOB=sinα,
三角形
四边形 OABC的面积为 .
∵0<α<π,
∴当 ,即 时,四边形 OABC的面积最大,
故得当 ,四边形 OABC的面积最大且最大值为 .
(2)△OAB中,
∴
∴ .
△OAC中,OC2=OA2+AC2﹣2OA?AC?cos∠OAC=
即
∵ ,
∴ ,即 时,OC有最大值.
16
故得当 时,OC有最大值 3.
22.已知函数
(1)若 m=1,n=0.求 y=f(x)的最小值;
(2)若 m=1,f(x)=0在[0,π]内有解.求实数 n的取值范围:
(3)若 n=0.求 y=f(x)的最大值 g(m).
【解答】(1)对于函数 f(x)=cos2x+mcos( ﹣x)+n=cos2x+msinx+n,
若 m=1,n=0,则函数 f(x)=cos2x+sinx,
当 ,k∈Z 时,cos2x和 sinx 同时取得最小值﹣1,
故 f(x)取得最小值为﹣2;
(2)若 m=1,f(x)=cos2x+sinx+n=0在[0,π]内有解,
故直线 y=n和曲线 y=﹣cos2x﹣sinx在[0,π]内有交点,
由 y=﹣cos2x﹣sinx=2sin2x﹣sinx﹣1,
令 sinx=t,t∈[0,1],则 y=2t2﹣t﹣1∈ ,
∴实数 n的取值范围是 ;
(3)若 n=0,则 f(x)=cos2x+msinx=﹣2sin2x+msinx+1,
令 sinx=t,t∈[﹣1,1],
则 y=﹣2t2+mt+1,对称轴方程为 t= .
当 <﹣1,即 m<﹣4时,g(m)=﹣m﹣1;
当﹣1 ,即﹣4≤m≤4,g(m)= ;
当 >1,即 m>4时,g(m)=m﹣1.
综上,g(m)=
