人教版七年级下册数学课件:7.1.2 平面直角坐标系 (共16张PPT)
文档属性
| 名称 | 人教版七年级下册数学课件:7.1.2 平面直角坐标系 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-04 11:47:17 | ||
图片预览



文档简介
(共16张PPT)
意志、悟性、想象力以及感觉上的一切作用,全由思维而来。
——笛卡尔
A
B
O
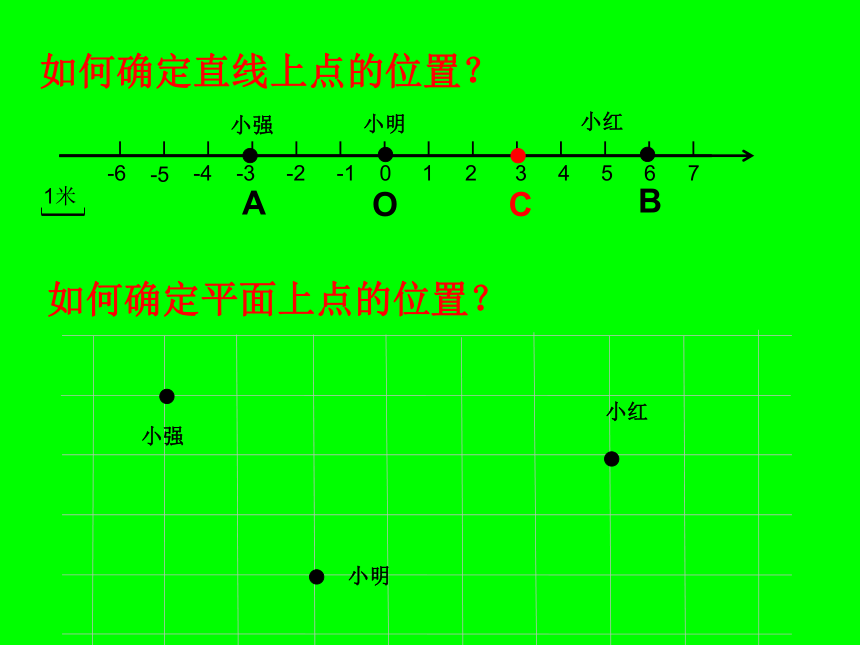
如何确定直线上点的位置?
小红
小明
小强
7.1.2 平面直角坐标系
自主探究
1.什么是平面直角坐标系?
2.什么是横轴、纵轴、坐标原点?
3.两坐标轴将平面分成几个部分?
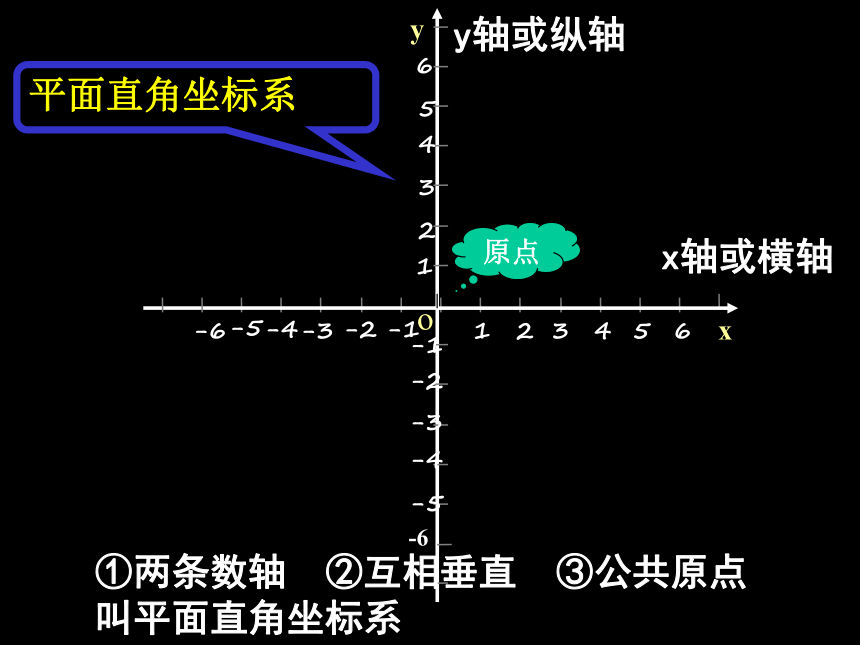
x轴或横轴
y轴或纵轴
原点
①两条数轴 ②互相垂直 ③公共原点 叫平面直角坐标系
平面直角坐标系
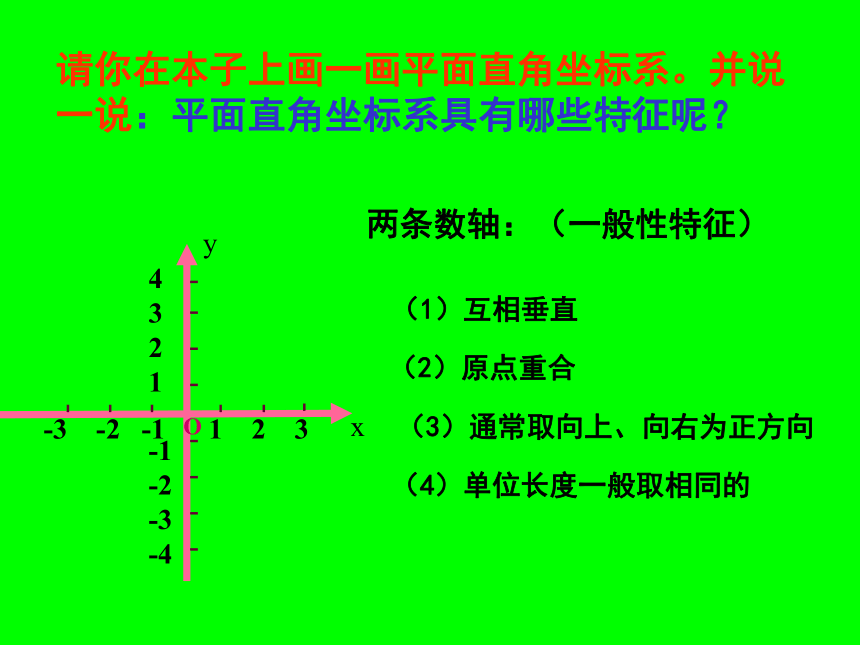
请你在本子上画一画平面直角坐标系。并说一说:平面直角坐标系具有哪些特征呢?
O
X
O
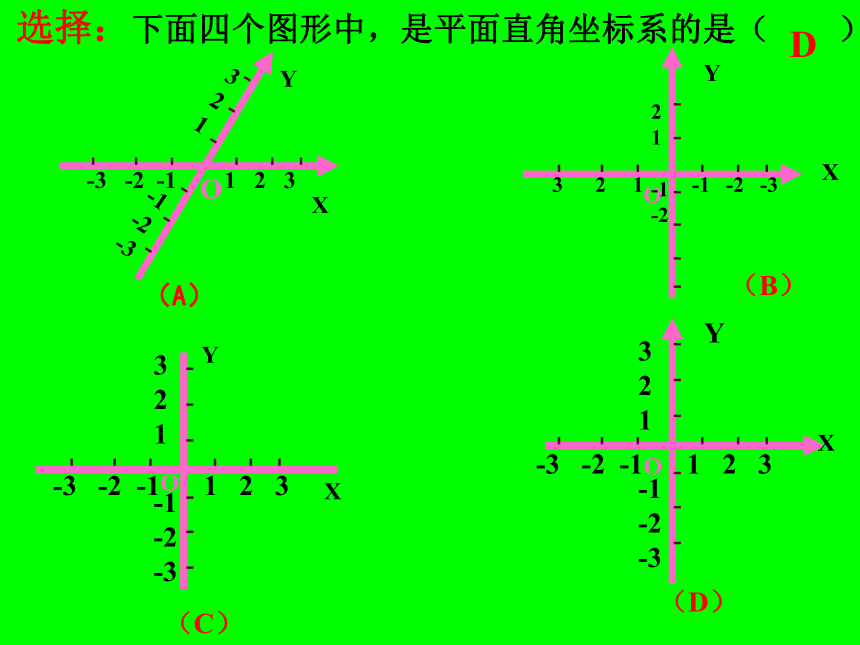
选择:下面四个图形中,是平面直角坐标系的是( )
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
Y
X
X
Y
(A)
3 2 1 -1 -2 -3
X
Y
(B)
2
1
-1
-2
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
(C)
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
Y
(D)
O
D
第一象限
第二象限
第三象限
第四象限
注 意:坐标轴上的点不属于任何象限。
·
A
A的横坐标为4
A的纵坐标为2
有序数对(4, 2)就叫做A的坐标
记作:A(4,2)
B(-4,1)
M
N
·
B
·
C
·
A
·
E
·
D
( 2,3 )
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
例1、写出图中A、B、C、D、E各点的坐标。
坐标是有序
数对。
1.下列各点分别在坐标平面的什么位置上?
A(3,2)
B(0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)
G(0、0)
第一象限
第三象限
第二象限
第四象限
y轴负半轴上
x轴负半轴上
原点
达标检测:
2.点A(0,-1)的位置在平面直角坐标系的 .
3.若点N(a+5,a-2)在x轴上,则点N的坐标为 .
y轴负半轴
(7, 0)
4.若点P(x,y)的坐标满足xy=0,则点p在( )
A.原点 B. x轴上 C. y轴上 D. x轴上或y轴上
D
火车站
兴林广场
县人民医院
第二中学
实验学校
客运站
南山广场
(0,3)
(3,1)
(-2,1)
(-2,-2)
(0,0)
(0,-5)
(4,-7)
5.已知点M(2,-3),则M到x轴的距离为 ,到y轴的距离为 .
6.已知点P到x轴和y轴的距离分别是2和5,求P点的坐标。
3
P(5,2) 或 P(5,-2) 或 P(-5,2)或P(-5,-2)
2
7.如图, 矩形ABCD的长宽分别是6 , 4 , 建立适当的坐标系,并写出各个顶点的坐标.
B
C
D
A
解:如图,以点C为坐标原点,分别以CD,CB所在的直线为x轴, y轴建立直角坐标系.此时C点坐标为(0,0)由CD长为6,CB长为4, 可得D,B,A的坐标分别为 D( 6,0 ),
B(0,4), A(6,4)
x
y
0
(0 , 0 )
( 0 , 4 )
( 6 , 4 )
( 6 , 0)
1
1
如图, 矩形ABCD的长宽分别是6 , 4 , 建立适当的坐标系,并写出各个顶点的坐标.
B
C
D
A
解:如图,分别以两对边中
点的连线为x轴,y轴建立
直角坐标系.此时各顶点
坐标为A(3,2),B(-3,2),
C(-3,-2),D(3,-2 ) .
x
y
0
(-3, -2 )
( -3 , 2)
( 3, 2 )
( 3 , -2)
1
1
意志、悟性、想象力以及感觉上的一切作用,全由思维而来。
——笛卡尔
A
B
O
如何确定直线上点的位置?
小红
小明
小强
7.1.2 平面直角坐标系
自主探究
1.什么是平面直角坐标系?
2.什么是横轴、纵轴、坐标原点?
3.两坐标轴将平面分成几个部分?
x轴或横轴
y轴或纵轴
原点
①两条数轴 ②互相垂直 ③公共原点 叫平面直角坐标系
平面直角坐标系
请你在本子上画一画平面直角坐标系。并说一说:平面直角坐标系具有哪些特征呢?
O
X
O
选择:下面四个图形中,是平面直角坐标系的是( )
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
Y
X
X
Y
(A)
3 2 1 -1 -2 -3
X
Y
(B)
2
1
-1
-2
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
(C)
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
Y
(D)
O
D
第一象限
第二象限
第三象限
第四象限
注 意:坐标轴上的点不属于任何象限。
·
A
A的横坐标为4
A的纵坐标为2
有序数对(4, 2)就叫做A的坐标
记作:A(4,2)
B(-4,1)
M
N
·
B
·
C
·
A
·
E
·
D
( 2,3 )
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
例1、写出图中A、B、C、D、E各点的坐标。
坐标是有序
数对。
1.下列各点分别在坐标平面的什么位置上?
A(3,2)
B(0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)
G(0、0)
第一象限
第三象限
第二象限
第四象限
y轴负半轴上
x轴负半轴上
原点
达标检测:
2.点A(0,-1)的位置在平面直角坐标系的 .
3.若点N(a+5,a-2)在x轴上,则点N的坐标为 .
y轴负半轴
(7, 0)
4.若点P(x,y)的坐标满足xy=0,则点p在( )
A.原点 B. x轴上 C. y轴上 D. x轴上或y轴上
D
火车站
兴林广场
县人民医院
第二中学
实验学校
客运站
南山广场
(0,3)
(3,1)
(-2,1)
(-2,-2)
(0,0)
(0,-5)
(4,-7)
5.已知点M(2,-3),则M到x轴的距离为 ,到y轴的距离为 .
6.已知点P到x轴和y轴的距离分别是2和5,求P点的坐标。
3
P(5,2) 或 P(5,-2) 或 P(-5,2)或P(-5,-2)
2
7.如图, 矩形ABCD的长宽分别是6 , 4 , 建立适当的坐标系,并写出各个顶点的坐标.
B
C
D
A
解:如图,以点C为坐标原点,分别以CD,CB所在的直线为x轴, y轴建立直角坐标系.此时C点坐标为(0,0)由CD长为6,CB长为4, 可得D,B,A的坐标分别为 D( 6,0 ),
B(0,4), A(6,4)
x
y
0
(0 , 0 )
( 0 , 4 )
( 6 , 4 )
( 6 , 0)
1
1
如图, 矩形ABCD的长宽分别是6 , 4 , 建立适当的坐标系,并写出各个顶点的坐标.
B
C
D
A
解:如图,分别以两对边中
点的连线为x轴,y轴建立
直角坐标系.此时各顶点
坐标为A(3,2),B(-3,2),
C(-3,-2),D(3,-2 ) .
x
y
0
(-3, -2 )
( -3 , 2)
( 3, 2 )
( 3 , -2)
1
1
