人教版数学七下5.2.2 平行线的判定课件(78张ppt)
文档属性
| 名称 | 人教版数学七下5.2.2 平行线的判定课件(78张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-04 18:14:28 | ||
图片预览








文档简介
(共78张PPT)
初一年级 数学
平行线的判定
平行
相交
平行线的定义
平行线的画法
平行公理及推论
同一平面内不重合的两条直线
复习回顾
垂直
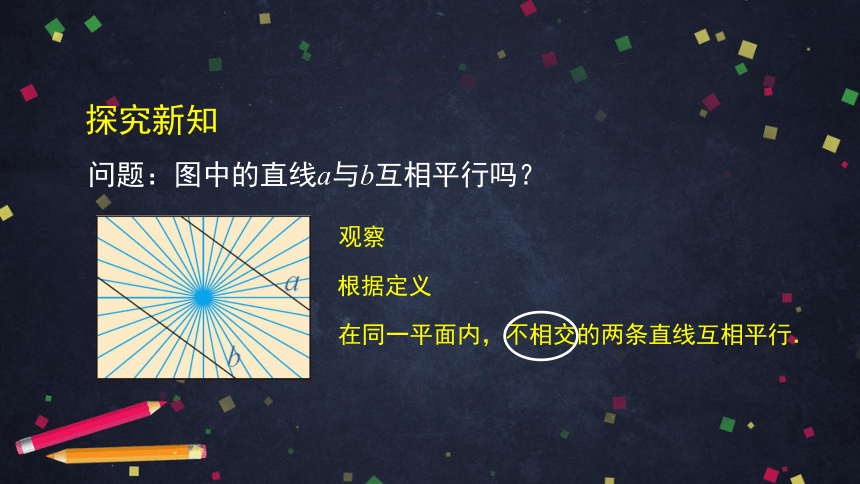
问题:图中的直线a与b互相平行吗?
a
b
探究新知
在同一平面内,不相交的两条直线互相平行.
观察
根据定义
问题:图中的直线a与b互相平行吗?
a
b
探究新知
难以直接根据定义来判断两条直线是否平行
探究新知
还有什么方法能判断两条直线是否平行?
A
B
C
D
如果AB∥EF,那么AB∥CD .
问题没有解决!
E
F
如何判断?
探究新知
再画一条与CD平行的直线EF,
A
B
C
D
还有什么方法能判断两条直线是否平行?
寻求新方法
探究新知
知识和经验
A
B
C
D
还有什么方法能判断两条直线是否平行?
B
C
A
D
O
类比垂直
数量关系
位置关系
探究新知
思考:可否由数量关系判定两条直线平行?
A
B
C
D
探究新知
数量关系
位置关系
a
c
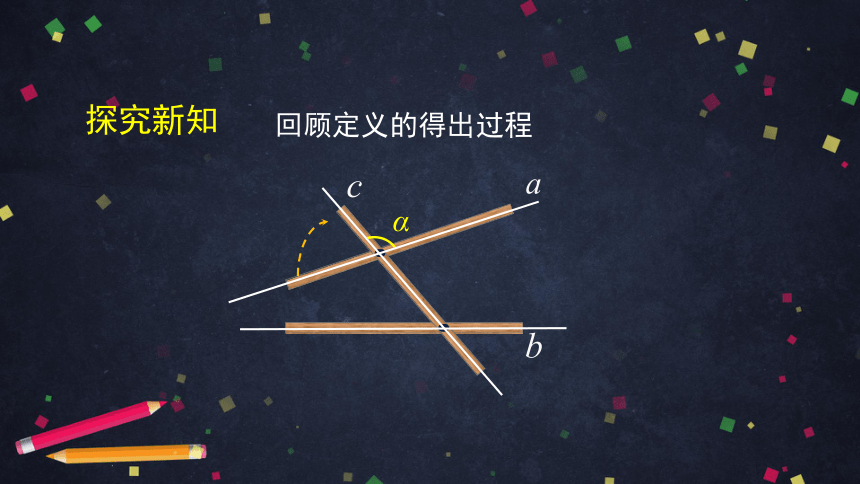
回顾定义的得出过程
探究新知
b
a
c
α
探究新知
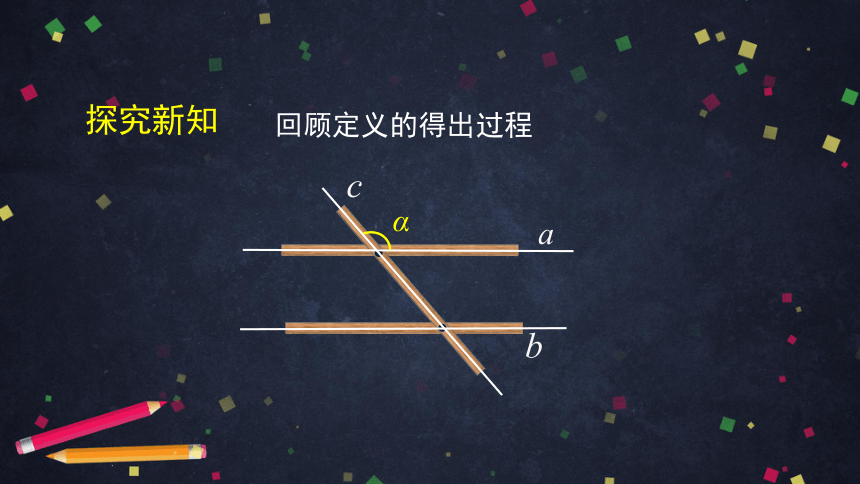
回顾定义的得出过程
b
α
c
探究新知
回顾定义的得出过程
a
b
a
b
c
转动a的过程中, 的度数也随之改变.
α
探究新知
回顾定义的得出过程
α
猜想:可以由数量关系判定两条直线平行.
A
B
C
D
探究新知
数量关系
判定平行
A
B
.
P
探究新知
回顾平行线的画法
A
B
.
P
探究新知
回顾平行线的画法
A
B
.
P
探究新知
回顾平行线的画法
A
B
.
P
1
探究新知
回顾平行线的画法
1
A
B
.
P
60°
探究新知
回顾平行线的画法
A
B
.
P
探究新知
回顾平行线的画法
A
B
.
P
2
探究新知
回顾平行线的画法
A
B
.
P
2
探究新知
回顾平行线的画法
A
B
.
P
2
探究新知
回顾平行线的画法
A
B
1
C
D
.
P
H
G
E
F
2
探究新知
60°
回顾平行线的画法
1
A
B
C
D
H
2
H
G
E
F
探究新知
回顾平行线的画法
.
P
关键因素
两个角相等
A
B
E
F
G
1
C
D
2
H
探究新知
对平行线画法的再认识
探究新知
A
B
C
D
E
F
G
H
2
1
∠1=∠2
AB∥CD
平行线的判定方法
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
同位角相等,两直线平行.
简单说成:
A
B
C
D
E
F
G
H
2
1
∠1=∠2
a∥b
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
c
a
b
2
1
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
因为∠1=∠2,
所以a∥b.
c
a
b
2
1
推理过程:
∠1和∠2是同位角
定义
判定
难以实现
发现问题
思路梳理
定义
判定
类比垂直
猜想
难以实现
发现问题
思路梳理
定义
判定
类比垂直
猜想
画平行线
判定方法
难以实现
发现问题
思路梳理
思考:有没有其他的判定方法?
再探新知
a
b
引入截线
借助同位角
思考:有没有其他的判定方法?
再探新知
a
b
c
同位角、内错角、同旁内角
两条直线被第三条直线所截
思考:有没有其他的判定方法?
再探新知
c
a
b
3
2
1
4
∠2和∠3是内错角
∠4和∠2是同旁内角
如果∠2=∠3,
能得出a∥b吗?
思考:有没有其他的判定方法?
再探新知
c
a
b
2
3
猜想:如果∠2=∠3,则a∥b.
再探新知
c
a
b
2
3
如何说明这个猜想是正确的?
猜想:如果∠2=∠3,则a∥b.
再探新知
c
a
b
2
3
猜想:如果∠2=∠3,则a∥b.
已经有什么
方法了?
再探新知
c
a
b
2
3
∠1=∠2
同位角相等,两直线平行.
猜想:如果∠2=∠3,则a∥b.
再探新知
c
a
b
2
1
3
猜想:如果∠2=∠3,则a∥b.
∠1=∠2
a∥b
已知∠2=∠3
?
再探新知
c
a
b
2
1
3
猜想:如果∠2=∠3,则a∥b.
已知∠2=∠3
再探新知
c
a
b
2
1
3
∠1=∠2
∠3和∠1应该有怎样的数量关系呢?
猜想:如果∠2=∠3,则a∥b.
已知∠2=∠3
再探新知
c
a
b
2
1
3
∠1=∠2
∠3=∠1
?
猜想:如果∠2=∠3,则a∥b.
c
a
b
2
1
3
∠3=∠1
再探新知
∠3和∠1是对顶角
∠3=∠1
∠2=∠3
∠1=∠2
a∥b
猜想:如果∠2=∠3,则a∥b.
再探新知
c
a
b
2
1
3
因为∠2=∠3,而∠3=∠1,
推理得出结论
再探新知
所以∠1=∠2.
从而a∥b.
c
a
b
2
1
3
c
a
b
2
1
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
内错角相等,两直线平行.
简单说成:
如图,
因为∠1=∠2,
所以a∥b.
c
a
b
2
1
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
内错角相等,两直线平行.
新问题
已解决的问题
转化
同位角相等,两直线平行.
提出问题
得出结论
猜想
推理
思路梳理
如图,∠2和∠4是一对同旁内角.
思考:它们满足怎样的数量关系时能判断a∥b?
再探新知
c
a
b
2
1
3
4
∠2=∠4?
再探新知
×
∠2+∠4=180°
c
a
b
2
1
3
4
猜想:如果∠2+∠4=180°, 则a∥b.
如何说明这个猜想是正确的?
再探新知
c
a
b
2
1
3
4
猜想:如果∠2+∠4=180°, 则a∥b.
判定方法1
同位角相等,两直线平行.
判定方法2
内错角相等,两直线平行.
再探新知
c
a
b
2
1
3
4
a∥b
∠1=∠2
或∠3=∠2
猜想:如果∠2+∠4=180°, 则a∥b.
再探新知
c
a
b
2
1
3
4
已知∠2+∠4=180°
?
a∥b
∠1=∠2
或∠3=∠2
猜想:如果∠2+∠4=180°, 则a∥b.
再探新知
c
a
b
2
1
3
4
已知∠2+∠4=180°
?
∠1=∠2
猜想:如果∠2+∠4=180°, 则a∥b.
再探新知
c
a
b
2
1
3
4
∠4和∠1是邻补角
猜想:如果∠2+∠4=180°, 则a∥b.
再探新知
∠4+∠1=180°
c
a
b
2
1
3
4
∠2+∠4=180°
∠4+∠1=180°
∠1=∠2
(同角的补角相等)
猜想:如果∠2+∠4=180°, 则a∥b.
再探新知
c
a
b
2
1
3
4
推理过程
因为∠2+∠4=180°,∠4+∠1=180°,
再探新知
从而a∥b.
所以∠1=∠2 .
c
a
b
2
1
3
4
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
c
a
b
2
1
简单说成:
同旁内角互补,两直线平行.
如图,
因为∠1+∠2=180°,
所以a∥b.
c
a
b
2
1
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
已知∠2+∠4=180°
?
a∥b
∠3=∠2
再探新知
能否利用“内错角相等,两直线平行”得到判定方法3呢?
c
a
b
2
1
3
4
∠2+∠4=180°
∠3=∠2
∠3+∠4=180°
(同角的补角相等)
能否利用“内错角相等,两直线平行”得到判定方法3呢?
再探新知
c
a
b
2
1
3
4
推理过程
所以∠3=∠2.
所以a∥b.
再探新知
因为∠2+∠4=180°,∠3+∠4=180°,
c
a
b
2
1
3
4
提出问题
得出结论
猜想
推理
已知∠2+∠4=180°
a∥b
∠1=∠2
或∠3=∠2
∠3+∠4=180°
∠4+∠1=180°
c
a
b
2
1
3
4
思路梳理
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定
角的数量关系
直线的位置关系
归纳总结
问题1 如图,你能说出木工用图中的角尺画平行线的道理吗?
解决问题
A
B
C
D
E
F
解答:用角尺画平行线实际上是画出了两个直角,根据“同位角相等(也可以根据内错角相等,同旁内角互补),两直线平行”,这样画出的就是平行线.
解决问题
A
B
C
D
E
F
A
D
B
E
C
O
问题2 如图,为了加固房屋,要在屋架上加一根横梁DE,
使DE∥BC,如果∠ABC=31°,∠ADE应为多少度?
D
B
E
C
A
角的数量关系
∠ABC=∠ADE
同位角
DE∥BC
答:∠ADE应为31°.
解决问题
A
B
C
D
平行线的判定
课堂小结
平行线的判定
E
F
利用同位角,内错角和同旁内角的数量关系即可判断AB,CD是否平行.
A
B
C
D
课堂小结
新问题
新方法
探究新方法
猜想
已有知识和学习经验
解决
解决不了
课堂小结
推理验证
判定方法2,判定方法3.
新问题
已解决的问题
转化
同位角相等,两直线平行.
提出问题
得出结论
猜想
推理
课堂小结
提出问题
得出结论
猜想
推理
隐含条件
结合已知
解决问题
课堂小结
图形
作业1
如图,这是小明同学自己制作的英语抄写纸的一部分,其中的横格线互相平行吗?你有多少种判别方法?
课后作业
作业2
通过本节课的学习,你觉得最大的收获是什么?遇到新问题时我们可以如何解决呢?
课后作业
同学们再见!
初一年级 数学
平行线的判定
平行
相交
平行线的定义
平行线的画法
平行公理及推论
同一平面内不重合的两条直线
复习回顾
垂直
问题:图中的直线a与b互相平行吗?
a
b
探究新知
在同一平面内,不相交的两条直线互相平行.
观察
根据定义
问题:图中的直线a与b互相平行吗?
a
b
探究新知
难以直接根据定义来判断两条直线是否平行
探究新知
还有什么方法能判断两条直线是否平行?
A
B
C
D
如果AB∥EF,那么AB∥CD .
问题没有解决!
E
F
如何判断?
探究新知
再画一条与CD平行的直线EF,
A
B
C
D
还有什么方法能判断两条直线是否平行?
寻求新方法
探究新知
知识和经验
A
B
C
D
还有什么方法能判断两条直线是否平行?
B
C
A
D
O
类比垂直
数量关系
位置关系
探究新知
思考:可否由数量关系判定两条直线平行?
A
B
C
D
探究新知
数量关系
位置关系
a
c
回顾定义的得出过程
探究新知
b
a
c
α
探究新知
回顾定义的得出过程
b
α
c
探究新知
回顾定义的得出过程
a
b
a
b
c
转动a的过程中, 的度数也随之改变.
α
探究新知
回顾定义的得出过程
α
猜想:可以由数量关系判定两条直线平行.
A
B
C
D
探究新知
数量关系
判定平行
A
B
.
P
探究新知
回顾平行线的画法
A
B
.
P
探究新知
回顾平行线的画法
A
B
.
P
探究新知
回顾平行线的画法
A
B
.
P
1
探究新知
回顾平行线的画法
1
A
B
.
P
60°
探究新知
回顾平行线的画法
A
B
.
P
探究新知
回顾平行线的画法
A
B
.
P
2
探究新知
回顾平行线的画法
A
B
.
P
2
探究新知
回顾平行线的画法
A
B
.
P
2
探究新知
回顾平行线的画法
A
B
1
C
D
.
P
H
G
E
F
2
探究新知
60°
回顾平行线的画法
1
A
B
C
D
H
2
H
G
E
F
探究新知
回顾平行线的画法
.
P
关键因素
两个角相等
A
B
E
F
G
1
C
D
2
H
探究新知
对平行线画法的再认识
探究新知
A
B
C
D
E
F
G
H
2
1
∠1=∠2
AB∥CD
平行线的判定方法
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
同位角相等,两直线平行.
简单说成:
A
B
C
D
E
F
G
H
2
1
∠1=∠2
a∥b
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
c
a
b
2
1
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
因为∠1=∠2,
所以a∥b.
c
a
b
2
1
推理过程:
∠1和∠2是同位角
定义
判定
难以实现
发现问题
思路梳理
定义
判定
类比垂直
猜想
难以实现
发现问题
思路梳理
定义
判定
类比垂直
猜想
画平行线
判定方法
难以实现
发现问题
思路梳理
思考:有没有其他的判定方法?
再探新知
a
b
引入截线
借助同位角
思考:有没有其他的判定方法?
再探新知
a
b
c
同位角、内错角、同旁内角
两条直线被第三条直线所截
思考:有没有其他的判定方法?
再探新知
c
a
b
3
2
1
4
∠2和∠3是内错角
∠4和∠2是同旁内角
如果∠2=∠3,
能得出a∥b吗?
思考:有没有其他的判定方法?
再探新知
c
a
b
2
3
猜想:如果∠2=∠3,则a∥b.
再探新知
c
a
b
2
3
如何说明这个猜想是正确的?
猜想:如果∠2=∠3,则a∥b.
再探新知
c
a
b
2
3
猜想:如果∠2=∠3,则a∥b.
已经有什么
方法了?
再探新知
c
a
b
2
3
∠1=∠2
同位角相等,两直线平行.
猜想:如果∠2=∠3,则a∥b.
再探新知
c
a
b
2
1
3
猜想:如果∠2=∠3,则a∥b.
∠1=∠2
a∥b
已知∠2=∠3
?
再探新知
c
a
b
2
1
3
猜想:如果∠2=∠3,则a∥b.
已知∠2=∠3
再探新知
c
a
b
2
1
3
∠1=∠2
∠3和∠1应该有怎样的数量关系呢?
猜想:如果∠2=∠3,则a∥b.
已知∠2=∠3
再探新知
c
a
b
2
1
3
∠1=∠2
∠3=∠1
?
猜想:如果∠2=∠3,则a∥b.
c
a
b
2
1
3
∠3=∠1
再探新知
∠3和∠1是对顶角
∠3=∠1
∠2=∠3
∠1=∠2
a∥b
猜想:如果∠2=∠3,则a∥b.
再探新知
c
a
b
2
1
3
因为∠2=∠3,而∠3=∠1,
推理得出结论
再探新知
所以∠1=∠2.
从而a∥b.
c
a
b
2
1
3
c
a
b
2
1
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
内错角相等,两直线平行.
简单说成:
如图,
因为∠1=∠2,
所以a∥b.
c
a
b
2
1
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
内错角相等,两直线平行.
新问题
已解决的问题
转化
同位角相等,两直线平行.
提出问题
得出结论
猜想
推理
思路梳理
如图,∠2和∠4是一对同旁内角.
思考:它们满足怎样的数量关系时能判断a∥b?
再探新知
c
a
b
2
1
3
4
∠2=∠4?
再探新知
×
∠2+∠4=180°
c
a
b
2
1
3
4
猜想:如果∠2+∠4=180°, 则a∥b.
如何说明这个猜想是正确的?
再探新知
c
a
b
2
1
3
4
猜想:如果∠2+∠4=180°, 则a∥b.
判定方法1
同位角相等,两直线平行.
判定方法2
内错角相等,两直线平行.
再探新知
c
a
b
2
1
3
4
a∥b
∠1=∠2
或∠3=∠2
猜想:如果∠2+∠4=180°, 则a∥b.
再探新知
c
a
b
2
1
3
4
已知∠2+∠4=180°
?
a∥b
∠1=∠2
或∠3=∠2
猜想:如果∠2+∠4=180°, 则a∥b.
再探新知
c
a
b
2
1
3
4
已知∠2+∠4=180°
?
∠1=∠2
猜想:如果∠2+∠4=180°, 则a∥b.
再探新知
c
a
b
2
1
3
4
∠4和∠1是邻补角
猜想:如果∠2+∠4=180°, 则a∥b.
再探新知
∠4+∠1=180°
c
a
b
2
1
3
4
∠2+∠4=180°
∠4+∠1=180°
∠1=∠2
(同角的补角相等)
猜想:如果∠2+∠4=180°, 则a∥b.
再探新知
c
a
b
2
1
3
4
推理过程
因为∠2+∠4=180°,∠4+∠1=180°,
再探新知
从而a∥b.
所以∠1=∠2 .
c
a
b
2
1
3
4
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
c
a
b
2
1
简单说成:
同旁内角互补,两直线平行.
如图,
因为∠1+∠2=180°,
所以a∥b.
c
a
b
2
1
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
已知∠2+∠4=180°
?
a∥b
∠3=∠2
再探新知
能否利用“内错角相等,两直线平行”得到判定方法3呢?
c
a
b
2
1
3
4
∠2+∠4=180°
∠3=∠2
∠3+∠4=180°
(同角的补角相等)
能否利用“内错角相等,两直线平行”得到判定方法3呢?
再探新知
c
a
b
2
1
3
4
推理过程
所以∠3=∠2.
所以a∥b.
再探新知
因为∠2+∠4=180°,∠3+∠4=180°,
c
a
b
2
1
3
4
提出问题
得出结论
猜想
推理
已知∠2+∠4=180°
a∥b
∠1=∠2
或∠3=∠2
∠3+∠4=180°
∠4+∠1=180°
c
a
b
2
1
3
4
思路梳理
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定
角的数量关系
直线的位置关系
归纳总结
问题1 如图,你能说出木工用图中的角尺画平行线的道理吗?
解决问题
A
B
C
D
E
F
解答:用角尺画平行线实际上是画出了两个直角,根据“同位角相等(也可以根据内错角相等,同旁内角互补),两直线平行”,这样画出的就是平行线.
解决问题
A
B
C
D
E
F
A
D
B
E
C
O
问题2 如图,为了加固房屋,要在屋架上加一根横梁DE,
使DE∥BC,如果∠ABC=31°,∠ADE应为多少度?
D
B
E
C
A
角的数量关系
∠ABC=∠ADE
同位角
DE∥BC
答:∠ADE应为31°.
解决问题
A
B
C
D
平行线的判定
课堂小结
平行线的判定
E
F
利用同位角,内错角和同旁内角的数量关系即可判断AB,CD是否平行.
A
B
C
D
课堂小结
新问题
新方法
探究新方法
猜想
已有知识和学习经验
解决
解决不了
课堂小结
推理验证
判定方法2,判定方法3.
新问题
已解决的问题
转化
同位角相等,两直线平行.
提出问题
得出结论
猜想
推理
课堂小结
提出问题
得出结论
猜想
推理
隐含条件
结合已知
解决问题
课堂小结
图形
作业1
如图,这是小明同学自己制作的英语抄写纸的一部分,其中的横格线互相平行吗?你有多少种判别方法?
课后作业
作业2
通过本节课的学习,你觉得最大的收获是什么?遇到新问题时我们可以如何解决呢?
课后作业
同学们再见!
