人教版数学七下 5.2.2平行线的判定的应用课件(53张ppt)
文档属性
| 名称 | 人教版数学七下 5.2.2平行线的判定的应用课件(53张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-04 18:15:08 | ||
图片预览








文档简介
(共53张PPT)
初一年级 数学
平行线的判定的应用
平行线的判定方法有哪些?
(1)定义.
(2)平行公理的推论 若a//b,b//c,则a//c.
(3)判定方法1 同位角相等,两直线平行.
(4)判定方法2 内错角相等,两直线平行.
(5)判定方法3 同旁内角互补,两直线平行.
复习回顾
平行线的判定方法
同位角相等, 两直线平行.
内错角相等, 两直线平行.
同旁内角互补,两直线平行.
特殊位置的角的数量关系
条件
复习回顾
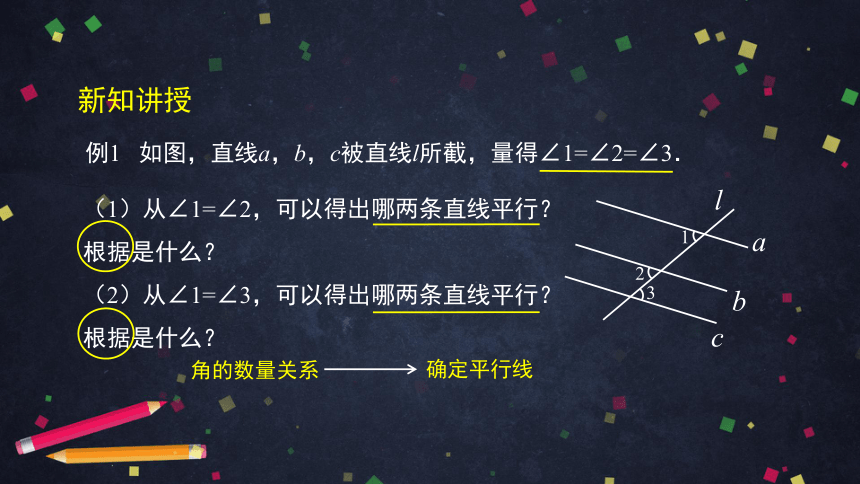
例1 如图,直线a,b,c被直线l所截,量得∠1=∠2=∠3.
新知讲授
a
b
c
1
l
2
3
(1)从∠1=∠2,可以得出哪两条直线平行?
根据是什么?
(2)从∠1=∠3,可以得出哪两条直线平行?
根据是什么?
角的数量关系
确定平行线
(1)从∠1=∠2,可以得出哪两条直线平行?
根据是什么?
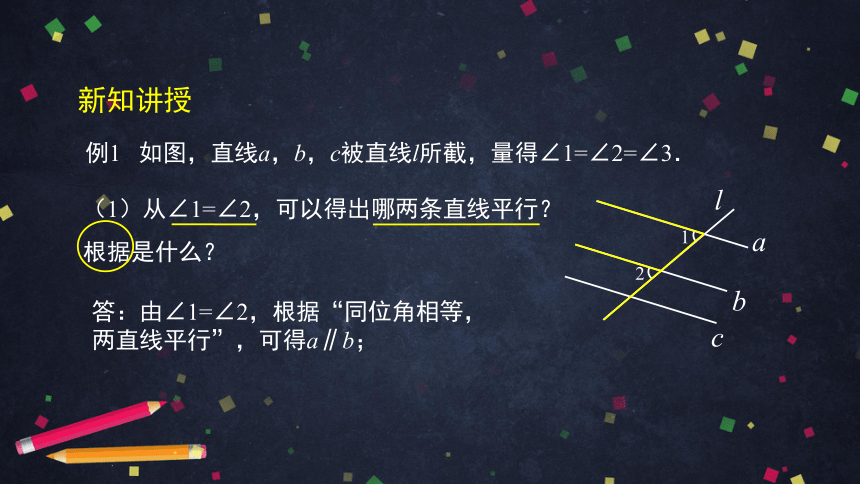
例1 如图,直线a,b,c被直线l所截,量得∠1=∠2=∠3.
新知讲授
a
b
c
1
l
2
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
被截线
(1)从∠1=∠2,可以得出哪两条直线平行?
根据是什么?
例1 如图,直线a,b,c被直线l所截,量得∠1=∠2=∠3.
新知讲授
识别角
a
b
c
1
l
2
角的边
确定截线
被截线:
直线a,b
∠1的两边所在直线:直线a,直线l
∠2的两边所在直线:直线b,直线l
截线
(1)从∠1=∠2,可以得出哪两条直线平行?
根据是什么?
例1 如图,直线a,b,c被直线l所截,量得∠1=∠2=∠3.
新知讲授
a
b
c
1
l
2
∠1和∠2是直线a,直线b被直线l所截形成的同位角
a∥b
a
b
c
1
l
2
例1 如图,直线a,b,c被直线l所截,量得∠1=∠2=∠3.
新知讲授
(1)从∠1=∠2,可以得出哪两条直线平行?
根据是什么?
答:由∠1=∠2,根据“同位角相等,
两直线平行”,可得a∥b;
例1 如图,直线a,b,c被直线l所截,量得∠1=∠2=∠3.
新知讲授
(2)从∠1=∠3,可以得出哪两条直线平行?
根据是什么?
a
b
c
1
l
3
∠1和∠3有怎样的位置关系
识别角
角的边
确定截线
被截线:
直线a,c
∠1的两边所在直线:直线a,直线l
∠3的两边所在直线:直线c,直线l
截线
例1 如图,直线a,b,c被直线l所截,量得∠1=∠2=∠3.
新知讲授
(2)从∠1=∠3,可以得出哪两条直线平行?
根据是什么?
a
b
c
1
l
3
∠1和∠3直线a,直线c被直线l所截形成的内错角
a∥c
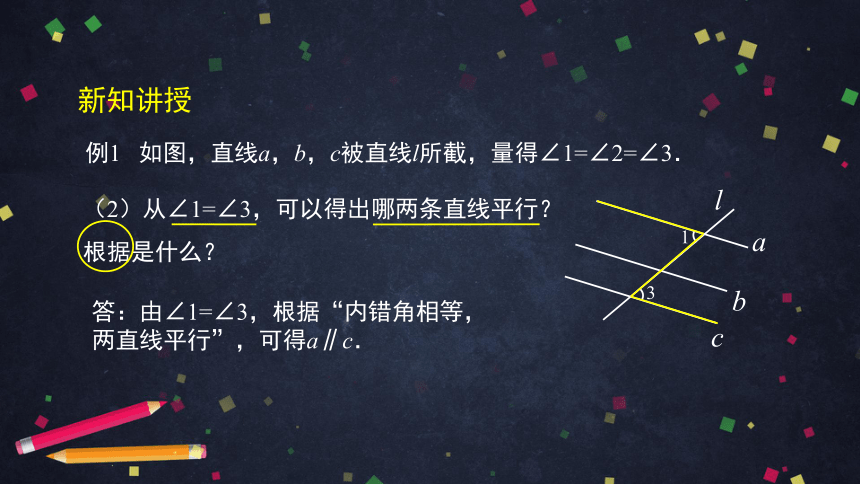
例1 如图,直线a,b,c被直线l所截,量得∠1=∠2=∠3.
新知讲授
(2)从∠1=∠3,可以得出哪两条直线平行?
根据是什么?
答:由∠1=∠3,根据“内错角相等,
两直线平行”,可得a∥c.
a
b
c
1
l
3
识别角
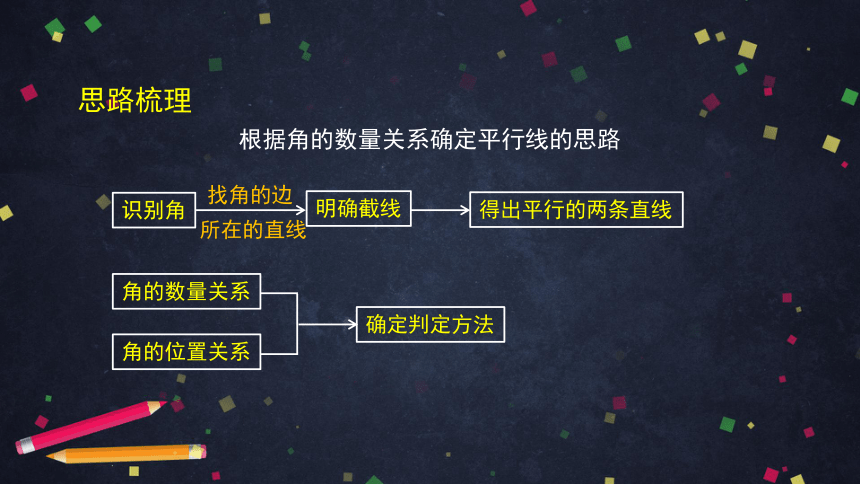
思路梳理
明确截线
得出平行的两条直线
找角的边
根据角的数量关系确定平行线的思路
所在的直线
角的数量关系
角的位置关系
确定判定方法
新知讲授
练习 如图,BE是AB的延长线.
(1)由∠CBE =∠A可以判定哪两条直线平行?根据是什么?
(2)由∠CBE =∠C可以判定哪两条直线平行?根据是什么?
角的数量关系
确定平行线
B
E
A
C
D
B
E
A
C
D
新知讲授
练习 如图,BE是AB的延长线.
(1)由∠CBE =∠A可以判定哪两条直线平行?根据是什么?
∠CBE两边所在直线:BC,BE
∠A两边所在直线:AD,AB
截线:AE
B
E
A
C
D
新知讲授
同位角相等,两直线平行
练习 如图,BE是AB的延长线.
(1)由∠CBE =∠A可以判定哪两条直线平行?根据是什么?
AD∥BC
B
E
A
C
D
新知讲授
练习 如图,BE是AB的延长线.
(2)由∠CBE =∠C可以判定哪两条直线平行?根据是什么?
内错角相等,两直线平行.
DC∥BE
例2 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线有怎样的位置关系?为什么?
新知讲授
画出图形
这两条直线平行
b
a
c
b⊥a
c⊥a
∠1=90°
∠2=90°
∠1=∠2
b∥c
新知讲授
例2 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线有怎样的位置关系?为什么?
2
1
b
a
c
用符号“∵”表示“因为”,
新知讲授
2
1
b
a
c
用符号“∵”表示“因为”,
符号“∴”表示“所以”.
新知讲授
2
1
b
a
c
答:这两条直线平行.理由如下:
如图,
∵b⊥a,
∴∠1=90°.
同理 ∠2=90° .
∴∠1=∠2 .
∵∠1和∠2是同位角,
∴b∥c (同位角相等,两直线平行) .
新知讲授
2
1
b
a
c
画图
猜想
得出结论
推理
解题小结
例2 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线有怎样的位置关系?为什么?
a
b
c
平行
角的数量关系
同位角相等
内错角相等
同旁内角互补
思考:你还能利用其它方法说明b∥c吗?
新知讲授
b
a
c
b⊥a
c⊥a
∠1=90°
∠3=90°
∠1=∠3
b∥c
∠1和∠3是内错角
新知讲授
b
a
c
3
1
推理如下:
如图,
∵b⊥a,
∴∠1=90°.
同理 ∠3=90° .
∴∠1=∠3 .
∵∠1和∠3是内错角,
∴b∥c (内错角相等,两直线平行).
新知讲授
b
a
c
3
1
平行
角的数量关系
同位角相等
内错角相等
同旁内角互补
新知讲授
思考:你还能利用其它方法说明b∥c吗?
b
a
c
b⊥a
c⊥a
∠1=90°
∠4=90°
∠1+∠4=180°
b∥c
∠1和∠4是同旁内角
新知讲授
b
a
c
同旁内角互补,两直线平行.
4
1
推理过程:
如图,
∵b⊥a,
∴∠1=90°.
同理 ∠4=90° .
∴∠1+∠4=180° .
∵∠1和∠4是同旁内角,
∴b∥c (同旁内角互补,两直线平行).
新知讲授
b
a
c
1
4
判定两条直线平行
选择方法
所需的条件
思路梳理
推理
已知
例2 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线有怎样的位置关系?为什么?
画图
猜想
得出结论
推理
b
a
c
找方法所需的条件
分析已知和未知
明确角的位置关系
选择方法判定两条直线平行
找角的边
思路梳理
平行线的判定的应用
所在直线
根据角的数量关系确定平行线
∠2+∠3=180°
a∥b
?
∠2和∠3不是同旁内角
巩固提升
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
3
a
c
b
4
5
1
2
(已知)
同位角相等
内错角相等
同旁内角互补
∠2+∠3=180°
a∥b
(已知)
?
巩固提升
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
∠4和∠3是同位角
3
a
c
b
4
5
1
2
∠2+∠3=180°
a∥b
∠4和∠3是同位角
∠4+∠2=180°
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
∠4=∠3
?
3
a
c
b
5
1
2
巩固提升
(已知)
4
∠2+∠3=180°
a∥b
(已知)
∠4+∠2=180°
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
∠4=∠3
3
a
c
b
5
1
2
巩固提升
4
答:当∠2+∠3=180°时,直线a,b平行.
理由如下:
如图,∵ ∠2+∠3=180°(已知),
∠2+∠4=180°(邻补角定义),
∴∠4=∠3 (同角的补角相等) .
∵∠4和∠3是同位角,
∴ a∥b (同位角相等,两直线平行) .
3
a
c
b
5
1
2
巩固提升
4
∠2+∠3=180°
(已知)
内错角相等
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
?
3
a
c
b
5
1
2
巩固提升
4
∠2+∠3=180°
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
∠4=∠5
∠4和∠5是内错角
?
3
a
c
b
5
1
2
巩固提升
∠3=∠5
∠4+∠2=180°
(已知)
4
∠2+∠3=180°
∠4=∠5
∠3=∠5
∠4+∠2=180°
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
?
3
a
c
b
5
1
2
巩固提升
4
∠2+∠3=180°
∠3=∠5
∠4+∠2=180°
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
3
a
c
b
5
1
2
巩固提升
∠2+∠5=180°
4
∠2+∠3=180°
∠3=∠5
∠4+∠2=180°
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
3
a
c
b
5
1
2
巩固提升
∠2+∠5=180°
4
∠2+∠3=180°
∠3=∠5
∠4+∠2=180°
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
3
a
c
b
5
1
2
巩固提升
∠2+∠5=180°
∠4=∠5
4
推理过程
如图,
∵ ∠2+∠3=180°(已知),
∠3=∠5(对顶角相等),
∴∠2+∠5 =180° .
∵∠2+∠4 =180°(邻补角定义),
∴∠4=∠5 (同角的补角相等).
∵∠4和∠5是内错角,
∴ a∥b (内错角相等,两直线平行) .
3
a
c
b
5
1
2
巩固提升
4
平行线判定的应用
条件不明显时
进行推理
挖掘图形中隐含条件
解决问题
思路梳理
找方法所需的条件
分析已知和未知
选择方法判定两条直线平行
结合已知
∠2+∠3=180°
a∥b
同旁内角互补
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
?
3
a
c
b
4
5
1
2
巩固提升
(已知)
∠2+∠3=180°
a∥b
同旁内角互补
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
∠5和∠6是同旁内角
?
3
a
c
b
4
5
1
6
2
巩固提升
(已知)
∠2+∠3=180°
(已知)
∠3=∠5
(对顶角相等)
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
3
a
c
b
4
5
1
6
2
巩固提升
∠2=∠6
同旁内角互补
a∥b
∠2+∠3=180°
(已知)
∠2=∠6
∠3=∠5
∠5+∠6=180°
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
3
a
c
b
4
5
1
6
2
巩固提升
a∥b
?
(对顶角相等)
∠2+∠3=180°
∠6
∠5
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
3
a
c
b
4
5
1
6
2
巩固提升
∠5+∠6=180°
a∥b
条件不直接时
进行推理
结合已知
挖掘图形中隐含条件
判定方法所需的条件
课堂小结
找方法所需的条件
分析已知和未知
选择方法判定两条直线平行
明确角的位置关系
找角的边
所在直线
根据角的数量关系确定平行线
平行线的判定的应用
课堂小结
分析已知和未知
题目特征
设计操作步骤
实施
反思总结
梳理思路方法
储备思路方法
解决
符合
解决问题的一般思路
1.如图,当∠1=∠2时,直线a,b平行吗?为什么?
a
c
b
2
作业
1
2.通过本节课的学习,你觉得最大的收获是什么?在应用平行线的判定的时候一般思路是什么?
作业
同学们再见!
初一年级 数学
平行线的判定的应用
平行线的判定方法有哪些?
(1)定义.
(2)平行公理的推论 若a//b,b//c,则a//c.
(3)判定方法1 同位角相等,两直线平行.
(4)判定方法2 内错角相等,两直线平行.
(5)判定方法3 同旁内角互补,两直线平行.
复习回顾
平行线的判定方法
同位角相等, 两直线平行.
内错角相等, 两直线平行.
同旁内角互补,两直线平行.
特殊位置的角的数量关系
条件
复习回顾
例1 如图,直线a,b,c被直线l所截,量得∠1=∠2=∠3.
新知讲授
a
b
c
1
l
2
3
(1)从∠1=∠2,可以得出哪两条直线平行?
根据是什么?
(2)从∠1=∠3,可以得出哪两条直线平行?
根据是什么?
角的数量关系
确定平行线
(1)从∠1=∠2,可以得出哪两条直线平行?
根据是什么?
例1 如图,直线a,b,c被直线l所截,量得∠1=∠2=∠3.
新知讲授
a
b
c
1
l
2
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
被截线
(1)从∠1=∠2,可以得出哪两条直线平行?
根据是什么?
例1 如图,直线a,b,c被直线l所截,量得∠1=∠2=∠3.
新知讲授
识别角
a
b
c
1
l
2
角的边
确定截线
被截线:
直线a,b
∠1的两边所在直线:直线a,直线l
∠2的两边所在直线:直线b,直线l
截线
(1)从∠1=∠2,可以得出哪两条直线平行?
根据是什么?
例1 如图,直线a,b,c被直线l所截,量得∠1=∠2=∠3.
新知讲授
a
b
c
1
l
2
∠1和∠2是直线a,直线b被直线l所截形成的同位角
a∥b
a
b
c
1
l
2
例1 如图,直线a,b,c被直线l所截,量得∠1=∠2=∠3.
新知讲授
(1)从∠1=∠2,可以得出哪两条直线平行?
根据是什么?
答:由∠1=∠2,根据“同位角相等,
两直线平行”,可得a∥b;
例1 如图,直线a,b,c被直线l所截,量得∠1=∠2=∠3.
新知讲授
(2)从∠1=∠3,可以得出哪两条直线平行?
根据是什么?
a
b
c
1
l
3
∠1和∠3有怎样的位置关系
识别角
角的边
确定截线
被截线:
直线a,c
∠1的两边所在直线:直线a,直线l
∠3的两边所在直线:直线c,直线l
截线
例1 如图,直线a,b,c被直线l所截,量得∠1=∠2=∠3.
新知讲授
(2)从∠1=∠3,可以得出哪两条直线平行?
根据是什么?
a
b
c
1
l
3
∠1和∠3直线a,直线c被直线l所截形成的内错角
a∥c
例1 如图,直线a,b,c被直线l所截,量得∠1=∠2=∠3.
新知讲授
(2)从∠1=∠3,可以得出哪两条直线平行?
根据是什么?
答:由∠1=∠3,根据“内错角相等,
两直线平行”,可得a∥c.
a
b
c
1
l
3
识别角
思路梳理
明确截线
得出平行的两条直线
找角的边
根据角的数量关系确定平行线的思路
所在的直线
角的数量关系
角的位置关系
确定判定方法
新知讲授
练习 如图,BE是AB的延长线.
(1)由∠CBE =∠A可以判定哪两条直线平行?根据是什么?
(2)由∠CBE =∠C可以判定哪两条直线平行?根据是什么?
角的数量关系
确定平行线
B
E
A
C
D
B
E
A
C
D
新知讲授
练习 如图,BE是AB的延长线.
(1)由∠CBE =∠A可以判定哪两条直线平行?根据是什么?
∠CBE两边所在直线:BC,BE
∠A两边所在直线:AD,AB
截线:AE
B
E
A
C
D
新知讲授
同位角相等,两直线平行
练习 如图,BE是AB的延长线.
(1)由∠CBE =∠A可以判定哪两条直线平行?根据是什么?
AD∥BC
B
E
A
C
D
新知讲授
练习 如图,BE是AB的延长线.
(2)由∠CBE =∠C可以判定哪两条直线平行?根据是什么?
内错角相等,两直线平行.
DC∥BE
例2 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线有怎样的位置关系?为什么?
新知讲授
画出图形
这两条直线平行
b
a
c
b⊥a
c⊥a
∠1=90°
∠2=90°
∠1=∠2
b∥c
新知讲授
例2 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线有怎样的位置关系?为什么?
2
1
b
a
c
用符号“∵”表示“因为”,
新知讲授
2
1
b
a
c
用符号“∵”表示“因为”,
符号“∴”表示“所以”.
新知讲授
2
1
b
a
c
答:这两条直线平行.理由如下:
如图,
∵b⊥a,
∴∠1=90°.
同理 ∠2=90° .
∴∠1=∠2 .
∵∠1和∠2是同位角,
∴b∥c (同位角相等,两直线平行) .
新知讲授
2
1
b
a
c
画图
猜想
得出结论
推理
解题小结
例2 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线有怎样的位置关系?为什么?
a
b
c
平行
角的数量关系
同位角相等
内错角相等
同旁内角互补
思考:你还能利用其它方法说明b∥c吗?
新知讲授
b
a
c
b⊥a
c⊥a
∠1=90°
∠3=90°
∠1=∠3
b∥c
∠1和∠3是内错角
新知讲授
b
a
c
3
1
推理如下:
如图,
∵b⊥a,
∴∠1=90°.
同理 ∠3=90° .
∴∠1=∠3 .
∵∠1和∠3是内错角,
∴b∥c (内错角相等,两直线平行).
新知讲授
b
a
c
3
1
平行
角的数量关系
同位角相等
内错角相等
同旁内角互补
新知讲授
思考:你还能利用其它方法说明b∥c吗?
b
a
c
b⊥a
c⊥a
∠1=90°
∠4=90°
∠1+∠4=180°
b∥c
∠1和∠4是同旁内角
新知讲授
b
a
c
同旁内角互补,两直线平行.
4
1
推理过程:
如图,
∵b⊥a,
∴∠1=90°.
同理 ∠4=90° .
∴∠1+∠4=180° .
∵∠1和∠4是同旁内角,
∴b∥c (同旁内角互补,两直线平行).
新知讲授
b
a
c
1
4
判定两条直线平行
选择方法
所需的条件
思路梳理
推理
已知
例2 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线有怎样的位置关系?为什么?
画图
猜想
得出结论
推理
b
a
c
找方法所需的条件
分析已知和未知
明确角的位置关系
选择方法判定两条直线平行
找角的边
思路梳理
平行线的判定的应用
所在直线
根据角的数量关系确定平行线
∠2+∠3=180°
a∥b
?
∠2和∠3不是同旁内角
巩固提升
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
3
a
c
b
4
5
1
2
(已知)
同位角相等
内错角相等
同旁内角互补
∠2+∠3=180°
a∥b
(已知)
?
巩固提升
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
∠4和∠3是同位角
3
a
c
b
4
5
1
2
∠2+∠3=180°
a∥b
∠4和∠3是同位角
∠4+∠2=180°
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
∠4=∠3
?
3
a
c
b
5
1
2
巩固提升
(已知)
4
∠2+∠3=180°
a∥b
(已知)
∠4+∠2=180°
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
∠4=∠3
3
a
c
b
5
1
2
巩固提升
4
答:当∠2+∠3=180°时,直线a,b平行.
理由如下:
如图,∵ ∠2+∠3=180°(已知),
∠2+∠4=180°(邻补角定义),
∴∠4=∠3 (同角的补角相等) .
∵∠4和∠3是同位角,
∴ a∥b (同位角相等,两直线平行) .
3
a
c
b
5
1
2
巩固提升
4
∠2+∠3=180°
(已知)
内错角相等
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
?
3
a
c
b
5
1
2
巩固提升
4
∠2+∠3=180°
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
∠4=∠5
∠4和∠5是内错角
?
3
a
c
b
5
1
2
巩固提升
∠3=∠5
∠4+∠2=180°
(已知)
4
∠2+∠3=180°
∠4=∠5
∠3=∠5
∠4+∠2=180°
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
?
3
a
c
b
5
1
2
巩固提升
4
∠2+∠3=180°
∠3=∠5
∠4+∠2=180°
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
3
a
c
b
5
1
2
巩固提升
∠2+∠5=180°
4
∠2+∠3=180°
∠3=∠5
∠4+∠2=180°
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
3
a
c
b
5
1
2
巩固提升
∠2+∠5=180°
4
∠2+∠3=180°
∠3=∠5
∠4+∠2=180°
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
3
a
c
b
5
1
2
巩固提升
∠2+∠5=180°
∠4=∠5
4
推理过程
如图,
∵ ∠2+∠3=180°(已知),
∠3=∠5(对顶角相等),
∴∠2+∠5 =180° .
∵∠2+∠4 =180°(邻补角定义),
∴∠4=∠5 (同角的补角相等).
∵∠4和∠5是内错角,
∴ a∥b (内错角相等,两直线平行) .
3
a
c
b
5
1
2
巩固提升
4
平行线判定的应用
条件不明显时
进行推理
挖掘图形中隐含条件
解决问题
思路梳理
找方法所需的条件
分析已知和未知
选择方法判定两条直线平行
结合已知
∠2+∠3=180°
a∥b
同旁内角互补
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
?
3
a
c
b
4
5
1
2
巩固提升
(已知)
∠2+∠3=180°
a∥b
同旁内角互补
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
∠5和∠6是同旁内角
?
3
a
c
b
4
5
1
6
2
巩固提升
(已知)
∠2+∠3=180°
(已知)
∠3=∠5
(对顶角相等)
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
3
a
c
b
4
5
1
6
2
巩固提升
∠2=∠6
同旁内角互补
a∥b
∠2+∠3=180°
(已知)
∠2=∠6
∠3=∠5
∠5+∠6=180°
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
3
a
c
b
4
5
1
6
2
巩固提升
a∥b
?
(对顶角相等)
∠2+∠3=180°
∠6
∠5
1.如图,当∠2+∠3=180°时,直线a,b平行吗?为什么?
3
a
c
b
4
5
1
6
2
巩固提升
∠5+∠6=180°
a∥b
条件不直接时
进行推理
结合已知
挖掘图形中隐含条件
判定方法所需的条件
课堂小结
找方法所需的条件
分析已知和未知
选择方法判定两条直线平行
明确角的位置关系
找角的边
所在直线
根据角的数量关系确定平行线
平行线的判定的应用
课堂小结
分析已知和未知
题目特征
设计操作步骤
实施
反思总结
梳理思路方法
储备思路方法
解决
符合
解决问题的一般思路
1.如图,当∠1=∠2时,直线a,b平行吗?为什么?
a
c
b
2
作业
1
2.通过本节课的学习,你觉得最大的收获是什么?在应用平行线的判定的时候一般思路是什么?
作业
同学们再见!
