人教A版(2019)必修 第一册第三章 3.1.2函数的表示法课件(30张ppt)
文档属性
| 名称 | 人教A版(2019)必修 第一册第三章 3.1.2函数的表示法课件(30张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-08 07:01:08 | ||
图片预览











文档简介
课件30张PPT。第三章 函数的概念与性质3.1.2 函数的表示法课程目标
1、明确函数的三种表示方法;
2、在实际情境中,会根据不同的需要选择恰当的方法表示函数;
3、通过具体实例,了解简单的分段函数,并能简单应用.
数学学科素养1.数学抽象:函数解析法及能由条件求出解析式;
2.逻辑推理:由条件求函数解析式;
3.数学运算:由函数解析式求值及函数解析式的计算;
4.数据分析:利用图像表示函数;
5.数学建模:由实际问题构建合理的函数模型。
自主预习,回答问题阅读课本67-68页,思考并完成以下问题
1.表示两个变量之间函数关系的方法有几种?分别是什么?
2.函数的各种表示法各有什么特点?
3.什么是分段函数?分段函数是一个还是几个函数?
?
4.怎样求分段函数的值?如何画分段函数的图象?
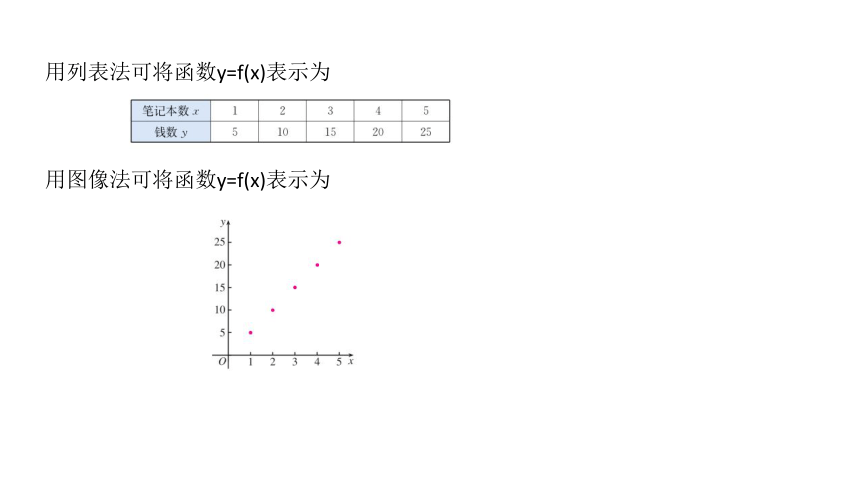
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。题型分析 举一反三题型一 函数的表示法例1 某种笔记本的单价是5元,买x (x∈{1,2, 3,4,5})个
笔记本需要y元.试用三种表示法表示函数y=f(x) .解:这个函数的定义域是数集{1,2, 3,4,5}.
用解析法可将函数y=f(x)表示为 y=5x, x∈{1,2, 3,4,5}用列表法可将函数y=f(x)表示为
用图像法可将函数y=f(x)表示为
解题方法(表示函数的注意事项)
1. 函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等等,注意判断一个图形是否是函数图象的依据;
2. 解析法:必须注明函数的定义域;
3 .图象法:是否连线;
4. 列表法:选取的自变量要有代表性,应能反映定义域的特征. 题型二 分段函数求值
例2:已知函数f (x)=
(1)求f 的值;
(2)若f(x)= ,求x的值.?[跟踪训练二]
1.题型三 求函数解析式
例3 .(1)已知f(x+1)=x2-3x+2,求f(x);
(2)已知f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x,求f(x)的解析式;
(3)已知函数f(x)对于任意的x都有f(x)+2f(-x)=3x-2,求f(x).解:(1)(方法一)令x+1=t,则x=t-1.
将x=t-1代入f(x+1)=x2-3x+2,
得f(t)=(t-1)2-3(t-1)+2=t2-5t+6,
∴f(x)=x2-5x+6.
(方法二)∵f(x+1)=x2-3x+2=x2+2x+1-5x-5+6=(x+1)2-5(x+1)+6,
∴f(x)=x2-5x+6.?解题方法(求函数解析式的四种常用方法)
1.直接法(代入法):已知f(x)的解析式,求f(g(x))的解析式,直接将g(x)代入即可.
2.待定系数法:若已知函数的类型,可用待定系数法求解,即由函数类型设出函数解析式,再根据条件列方程(或方程组),通过解方程(组)求出待定系数,进而求出函数解析式.
3.换元法(有时可用“配凑法”):已知函数f(g(x))的解析式求f(x)的解析式可用换元法(或“配凑法”),即令g(x)=t,反解出x,然后代入f(g(x))中求出f(t),从而求出f(x).
4.解方程组法或消元法:在已知式子中,含有关于两个不同变量的函数,而这两个变量有着某种关系,这时就要依据两个变量的关系,建立一个新的关于两个变量的式子,由两个式子建立方程组,通过解方程组消去一个变量,得到目标变量的解析式,这种方法叫做解方程组法或消元法.????题型四 函数的图像及应用
例4 1. 函数f(x)=|x-1|的图象是( )
???解题方法(函数图像问题处理措施)
(1)若y=f(x)是已学过的基本初等函数,则描出图象上的几个关键点,直接画出图象即可,有些可能需要根据定义域进行取舍.
(2)若y=f(x)不是所学过的基本初等函数之一,则要按:①列表;②描点;③连线三个基本步骤作出y=f(x)的图象.
(3)作分段函数的图象时,分别作出各段的图象,在作每一段图象时,先不管定义域的限制,作出其图象,再保留定义域内的一段图象即可,作图时要特别注意接点处点的虚实,保证不重不漏.
?题型五 函数的实际应用
例5下表是某校高一(1)班三位同学在高一学年度几次数学
测试的成绩及班级及班级平均分表:
请你对这三们同学在高一学年度的数学学习情况做一个分析.解:从表可以知道每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况。如果将每位同学的“成绩”与“测试序号”之间的函数关系分别用图象(均为6个离散的点)表示出来,如图3.1-6,那么就能直观地看到每位同学成绩变化的情况,这对我们的分析很有帮助.
从图3.1-6可以看到,王伟同学的数学学习成绩始终高于班级平均水平,学习情况比较稳定而且成绩优秀.张城同学的数学学习成绩不稳定,总是在班级平均水平上下波动,而且波动幅度较大.赵磊同学的数学学习成绩低于班级平均水平,但表示他成绩变化的图象呈上升趋势,表明他的数学成绩在稳步提高.
2、在实际情境中,会根据不同的需要选择恰当的方法表示函数;
3、通过具体实例,了解简单的分段函数,并能简单应用.
数学学科素养1.数学抽象:函数解析法及能由条件求出解析式;
2.逻辑推理:由条件求函数解析式;
3.数学运算:由函数解析式求值及函数解析式的计算;
4.数据分析:利用图像表示函数;
5.数学建模:由实际问题构建合理的函数模型。
自主预习,回答问题阅读课本67-68页,思考并完成以下问题
1.表示两个变量之间函数关系的方法有几种?分别是什么?
2.函数的各种表示法各有什么特点?
3.什么是分段函数?分段函数是一个还是几个函数?
?
4.怎样求分段函数的值?如何画分段函数的图象?
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。题型分析 举一反三题型一 函数的表示法例1 某种笔记本的单价是5元,买x (x∈{1,2, 3,4,5})个
笔记本需要y元.试用三种表示法表示函数y=f(x) .解:这个函数的定义域是数集{1,2, 3,4,5}.
用解析法可将函数y=f(x)表示为 y=5x, x∈{1,2, 3,4,5}用列表法可将函数y=f(x)表示为
用图像法可将函数y=f(x)表示为
解题方法(表示函数的注意事项)
1. 函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等等,注意判断一个图形是否是函数图象的依据;
2. 解析法:必须注明函数的定义域;
3 .图象法:是否连线;
4. 列表法:选取的自变量要有代表性,应能反映定义域的特征. 题型二 分段函数求值
例2:已知函数f (x)=
(1)求f 的值;
(2)若f(x)= ,求x的值.?[跟踪训练二]
1.题型三 求函数解析式
例3 .(1)已知f(x+1)=x2-3x+2,求f(x);
(2)已知f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x,求f(x)的解析式;
(3)已知函数f(x)对于任意的x都有f(x)+2f(-x)=3x-2,求f(x).解:(1)(方法一)令x+1=t,则x=t-1.
将x=t-1代入f(x+1)=x2-3x+2,
得f(t)=(t-1)2-3(t-1)+2=t2-5t+6,
∴f(x)=x2-5x+6.
(方法二)∵f(x+1)=x2-3x+2=x2+2x+1-5x-5+6=(x+1)2-5(x+1)+6,
∴f(x)=x2-5x+6.?解题方法(求函数解析式的四种常用方法)
1.直接法(代入法):已知f(x)的解析式,求f(g(x))的解析式,直接将g(x)代入即可.
2.待定系数法:若已知函数的类型,可用待定系数法求解,即由函数类型设出函数解析式,再根据条件列方程(或方程组),通过解方程(组)求出待定系数,进而求出函数解析式.
3.换元法(有时可用“配凑法”):已知函数f(g(x))的解析式求f(x)的解析式可用换元法(或“配凑法”),即令g(x)=t,反解出x,然后代入f(g(x))中求出f(t),从而求出f(x).
4.解方程组法或消元法:在已知式子中,含有关于两个不同变量的函数,而这两个变量有着某种关系,这时就要依据两个变量的关系,建立一个新的关于两个变量的式子,由两个式子建立方程组,通过解方程组消去一个变量,得到目标变量的解析式,这种方法叫做解方程组法或消元法.????题型四 函数的图像及应用
例4 1. 函数f(x)=|x-1|的图象是( )
???解题方法(函数图像问题处理措施)
(1)若y=f(x)是已学过的基本初等函数,则描出图象上的几个关键点,直接画出图象即可,有些可能需要根据定义域进行取舍.
(2)若y=f(x)不是所学过的基本初等函数之一,则要按:①列表;②描点;③连线三个基本步骤作出y=f(x)的图象.
(3)作分段函数的图象时,分别作出各段的图象,在作每一段图象时,先不管定义域的限制,作出其图象,再保留定义域内的一段图象即可,作图时要特别注意接点处点的虚实,保证不重不漏.
?题型五 函数的实际应用
例5下表是某校高一(1)班三位同学在高一学年度几次数学
测试的成绩及班级及班级平均分表:
请你对这三们同学在高一学年度的数学学习情况做一个分析.解:从表可以知道每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况。如果将每位同学的“成绩”与“测试序号”之间的函数关系分别用图象(均为6个离散的点)表示出来,如图3.1-6,那么就能直观地看到每位同学成绩变化的情况,这对我们的分析很有帮助.
从图3.1-6可以看到,王伟同学的数学学习成绩始终高于班级平均水平,学习情况比较稳定而且成绩优秀.张城同学的数学学习成绩不稳定,总是在班级平均水平上下波动,而且波动幅度较大.赵磊同学的数学学习成绩低于班级平均水平,但表示他成绩变化的图象呈上升趋势,表明他的数学成绩在稳步提高.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
