人教版八年级下册数学18.1.1平行四边形的性质课件 (18张PPT)
文档属性
| 名称 | 人教版八年级下册数学18.1.1平行四边形的性质课件 (18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-05 08:46:05 | ||
图片预览



文档简介
(共18张PPT)
在数学的天地里,重要的不 是我们知道什么,而是我们怎么知道什么。 ——毕达哥拉斯
“有种图形生的怪,有棱有角扁脑袋;
上下左右共四边,两两平行围起来。”
(打一图形)
你还能举出平行四边形在生活中应用的例子吗?
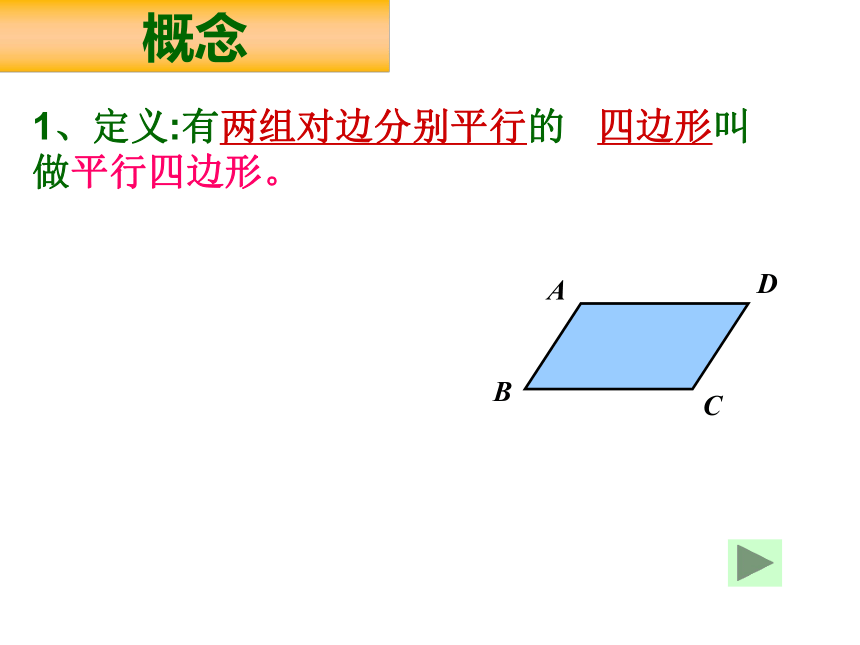
概念
1、定义:有两组对边分别平行的 四边形叫做平行四边形。
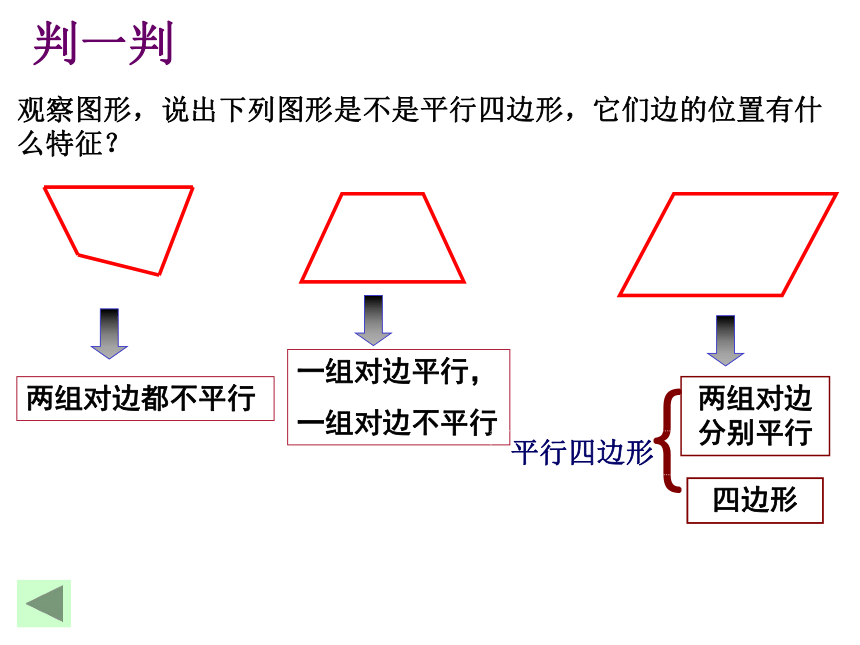
两组对边都不平行
一组对边平行,
一组对边不平行
观察图形,说出下列图形是不是平行四边形,它们边的位置有什么特征?
两组对边
分别平行
四边形
{
平行四边形
判一判
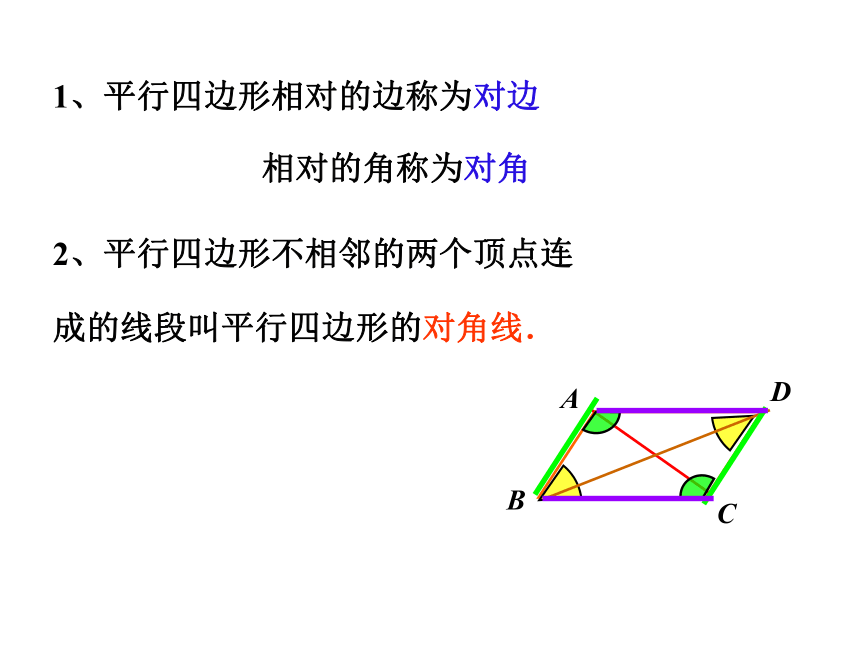
1、平行四边形相对的边称为对边
相对的角称为对角
表示方法
如图平行四边形ABCD
2、表示:
ABCD
3、读作:平行四边形ABCD
4、几何语言:
AB∥CD AD∥BC
四边形ABCD是平行四边形
1、两要素:
同桌两个同学合作根据定义画一个平行四边形,然后用直尺,量角器等工具度量你刚才画的平行四边形的边和角,并记录下数据,猜想平行四边形的对边对角之间的关系?
画一画,量一量
猜想
结论:
1.平行四边形的两组对边相等
2.平行四边形的两组对角相等。
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
从拼图可以得到什么启示?
小结:平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
即∠BAD=∠DCB
证明:连结AC
∵AB∥CD,AD∥BC(平行四边形的对边平行)
∴∠1=∠2,∠3=∠4
∠1=∠2,
AC=CA,
∠3=∠4
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
A
B
C
D
性质2:
平行四边形的两组对角分别相等。
性质1:
平行四边形的两组对边分别相等。
性质3:平行四边形是中心对称图形
互补
探究
旋转平行四边形,探究对称性
平行四边形是中心对称图形.
例1 如图,在 ABCD中DE⊥AB,BF⊥CD,垂足分别为E,F.求证AE=CF.
A
B
C
D
E
F
∵四边形ABCD是平行四边形,
∴∠A=∠C, AD=CB
又∵∠AED=∠CFB=90°
∴ ADE ≌ CBF(AAS)
∠A=∠C
∠AED=∠CFB=90°
AD=CB
∴AE=CF
证明:
例题教学
解:
例
题
教
学
平行四边形的两组对边相等;
平行四边形的两组对角相等;邻角互补。
平行四边形是中心对称图形。
有两组对边分别平行的四边形是平行四边形。
课后作业
P43练习1.
P49复习巩固1.
在数学的天地里,重要的不 是我们知道什么,而是我们怎么知道什么。 ——毕达哥拉斯
“有种图形生的怪,有棱有角扁脑袋;
上下左右共四边,两两平行围起来。”
(打一图形)
你还能举出平行四边形在生活中应用的例子吗?
概念
1、定义:有两组对边分别平行的 四边形叫做平行四边形。
两组对边都不平行
一组对边平行,
一组对边不平行
观察图形,说出下列图形是不是平行四边形,它们边的位置有什么特征?
两组对边
分别平行
四边形
{
平行四边形
判一判
1、平行四边形相对的边称为对边
相对的角称为对角
表示方法
如图平行四边形ABCD
2、表示:
ABCD
3、读作:平行四边形ABCD
4、几何语言:
AB∥CD AD∥BC
四边形ABCD是平行四边形
1、两要素:
同桌两个同学合作根据定义画一个平行四边形,然后用直尺,量角器等工具度量你刚才画的平行四边形的边和角,并记录下数据,猜想平行四边形的对边对角之间的关系?
画一画,量一量
猜想
结论:
1.平行四边形的两组对边相等
2.平行四边形的两组对角相等。
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
从拼图可以得到什么启示?
小结:平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
即∠BAD=∠DCB
证明:连结AC
∵AB∥CD,AD∥BC(平行四边形的对边平行)
∴∠1=∠2,∠3=∠4
∠1=∠2,
AC=CA,
∠3=∠4
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
A
B
C
D
性质2:
平行四边形的两组对角分别相等。
性质1:
平行四边形的两组对边分别相等。
性质3:平行四边形是中心对称图形
互补
探究
旋转平行四边形,探究对称性
平行四边形是中心对称图形.
例1 如图,在 ABCD中DE⊥AB,BF⊥CD,垂足分别为E,F.求证AE=CF.
A
B
C
D
E
F
∵四边形ABCD是平行四边形,
∴∠A=∠C, AD=CB
又∵∠AED=∠CFB=90°
∴ ADE ≌ CBF(AAS)
∠A=∠C
∠AED=∠CFB=90°
AD=CB
∴AE=CF
证明:
例题教学
解:
例
题
教
学
平行四边形的两组对边相等;
平行四边形的两组对角相等;邻角互补。
平行四边形是中心对称图形。
有两组对边分别平行的四边形是平行四边形。
课后作业
P43练习1.
P49复习巩固1.
