人教版八年级数学下册-第十八章《平行四边形》单元测试(含答案)
文档属性
| 名称 | 人教版八年级数学下册-第十八章《平行四边形》单元测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 101.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-04 17:02:57 | ||
图片预览


文档简介
第十八章《平行四边形》单元测试
姓名: 班级: 座号:
一、单选题(共8题;共32分)
1.平行四边形所具有的性质是( ?? )
A.?对角线相等???????????B.?邻边互相垂直???????????C.?每条对角线平分一组对角???????????D.?两组对边分别相等
2.在四边形ABCD中,对角线AC与BD交于点O,下列条件不能判定这个四边形是平行四边形的是(? )
A.?OA=OC,OB=OD????????B.?AD∥BC,AB∥DC??????????C.?AB=DC,AD=BC????????D.?AB∥DC,AD=BC
3.正方形具有而菱形不一定具有的性质是(?? ).
A.?四条边都相等???????????B.?对角线互相垂直且平分???????????C.?对角线相等???????????D.?对角线平分一组对角
4.在四边形ABCD中,现有以下条件:①AB//CD,②A B=CD,③BC//AD,④BC=AD,从中任选两个使四边形ABCD为平行四边形的选法有(?? ).
A.?3种???????????????????????????????????????B.?4种???????????????????????????????????????C.?5种???????????????????????????????????????D.?6种
5.如图,矩形ABCD的对角线AC,BD相交于点O,如果△ABC的周长比△AOB的周长长10厘米,则矩形边AD的长是(?? ? )
A.?5厘米???????????????????????????????B.?10厘米???????????????????????????????C.?7.5厘米???????????????????????????????D.?不能确定
6.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是(?? )
A.?30?????????????????????????????????????????B.?34?????????????????????????????????????????C.?36?????????????????????????????????????????D.?40
7.如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为6和8,那么点P到矩形的两条对角线AC和BD的距离之和是(? )
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?无法确定
8.如图,点 、 分别是正方形 的边 、 上的点,且 , 、 相交于点 ,下列结论:① ;② ;③ ,其中一定正确的有(?? )
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
二、填空题(共8题;共24分)
1.在 ABCD中,若AB=3cm,AD=4cm,则它的周长为________cm.
2.已知一个菱形的两条对角线的长分别为5cm和8cm,该菱形的面积为________cm2 .
3.工人师博常常通过测量平行四边形零件的对角线是否相等来检验零件是否为矩形,请问工人师博此种检验方法依据的道理是________.
4.如图,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有________种.
5.如图,在四边形ABCD中,对角线AC、BD相交于点O,且AO=CO,BO=DO,要使四边形ABCD为矩形,则需添加的条件为________(填一个即可).
6如图,在四边形ABCD中,AB=BC=CD=DA , 对角线AC与BD相交于点O , 若不增加任何字母与辅助线,要使四边形ABCD是正方形,则还需增加一个条件是________?
7.如图,在平行四边形ABCD中,∠A与∠B的度数之比为2:1,则∠A=________°
8.如图,直线过正方形ABCD的顶点B,点A、C到直E的距离分别是1和2,则正方形ABCD面积是________.
三、解答题(共44分)
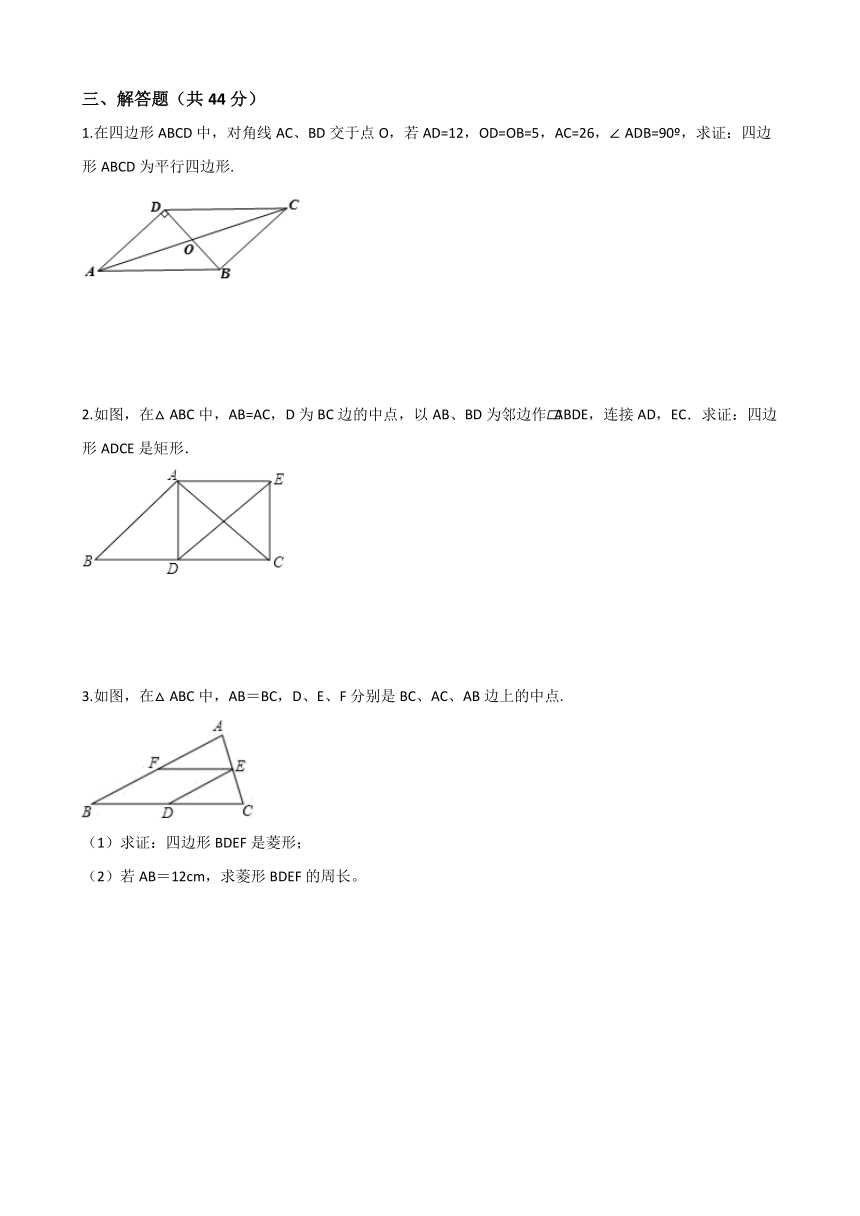
1.在四边形ABCD中,对角线AC、BD交于点O,若AD=12,OD=OB=5,AC=26,∠ADB=90?,求证:四边形ABCD为平行四边形.
2.如图,在△ABC中,AB=AC,D为BC边的中点,以AB、BD为邻边作?ABDE,连接AD,EC.求证:四边形ADCE是矩形.
3.如图,在△ABC中,AB=BC,D、E、F分别是BC、AC、AB边上的中点.
(1)求证:四边形BDEF是菱形;
(2)若AB=12cm,求菱形BDEF的周长。
4.如图,正方形ABCD中,E,F分别在AD,DC上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;
(1)求证:∠ABE= ∠BGE;
(3)若AB=4,AE=1,求S△BEG 。
5.如图,已知: , , ,
(1)图中有几个平行四边形?将它们分别表示出来。
(2)在(1)中选择一个进行证明。
(3)证明: 是 边上的中点。
答案
一、1—8 DDCBB BCC
二、
1. 14
2. 20
3. 对角线相等的平行四边形是矩形
4. 4
5. ∠DAB=90°
6. AC=BD或AB⊥BC(答案不唯一)
7. 120
8. 5
三、1. 证明:∵AD=12,OD=5,∠ADB=90°,
∴AO=13,
∵AC=26,
∴AO=OC=13,且DO=OB=5,
∴四边形ABCD为平行四边形
2.证明:∵AB=AC,D为BC边的中点,
∴AD⊥BC,BD=CD,
∴∠ADC=90°,
∵四边形ABDE是平行四边形,
∴AE∥BD,AE=BD,
∴AE∥CD,AE=CD,
∴四边形ADCE是平行四边形,
又∵∠ADC=90°,
∴四边形ADCE是矩形
3. (1)证明:∵D、E、F分别是BC、AC、AB的中点,
∴DE∥AB,EF∥BC,
∴四边形BDEF是平行四边形,
又∵DE= AB,EF= BC,且AB=BC,
∴DE=EF,
∴四边形BDEF是菱形;
(2)解:∵AB=12cm,F为AB中点,
∴BF=6cm,
∴菱形BDEF的周长为6×4=24cm.
4. (1)解:作GM⊥BE于M.
∵四边形ABCD是正方形,
∴AB=BC=4,∠A=∠ABC=∠BMG=90°,AD∥BG,
∵∠AEB=∠BEG,∠AEB=∠EBG,
∴∠BEG=∠EBG,
∴GE=GB,∵GM⊥EB,
∴∠MGB=∠MBE,BM=EM,
∵∠ABE+∠EBG=90°,∠EBG+∠MGB=90°,
∴∠ABE=∠MGB= ∠EGB
(2)解:在Rt△ABE中,BE= = = ,∴BM= ,
∵∠ABE=∠MGB,∠A=∠GMB=90°,
∴△ABE∽△MGB,
∴ = ,
∴ = ,
∴GM=2 ,
∴S△EBG= × ×2 =17.
5 (1)解:∵AB∥DF,ED∥BC,EF∥AC,
∴图中共有3个平行四边形,即 、 、 ;
(2)解:∵AB∥DF,EF∥AC,
∴AE∥DF,EF∥AD,
∴四边形AEFD是平行四边形.
(3)证明:四边形 和四边形 都是平行四边形,
?
?
是 边上的中点.
姓名: 班级: 座号:
一、单选题(共8题;共32分)
1.平行四边形所具有的性质是( ?? )
A.?对角线相等???????????B.?邻边互相垂直???????????C.?每条对角线平分一组对角???????????D.?两组对边分别相等
2.在四边形ABCD中,对角线AC与BD交于点O,下列条件不能判定这个四边形是平行四边形的是(? )
A.?OA=OC,OB=OD????????B.?AD∥BC,AB∥DC??????????C.?AB=DC,AD=BC????????D.?AB∥DC,AD=BC
3.正方形具有而菱形不一定具有的性质是(?? ).
A.?四条边都相等???????????B.?对角线互相垂直且平分???????????C.?对角线相等???????????D.?对角线平分一组对角
4.在四边形ABCD中,现有以下条件:①AB//CD,②A B=CD,③BC//AD,④BC=AD,从中任选两个使四边形ABCD为平行四边形的选法有(?? ).
A.?3种???????????????????????????????????????B.?4种???????????????????????????????????????C.?5种???????????????????????????????????????D.?6种
5.如图,矩形ABCD的对角线AC,BD相交于点O,如果△ABC的周长比△AOB的周长长10厘米,则矩形边AD的长是(?? ? )
A.?5厘米???????????????????????????????B.?10厘米???????????????????????????????C.?7.5厘米???????????????????????????????D.?不能确定
6.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是(?? )
A.?30?????????????????????????????????????????B.?34?????????????????????????????????????????C.?36?????????????????????????????????????????D.?40
7.如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为6和8,那么点P到矩形的两条对角线AC和BD的距离之和是(? )
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?无法确定
8.如图,点 、 分别是正方形 的边 、 上的点,且 , 、 相交于点 ,下列结论:① ;② ;③ ,其中一定正确的有(?? )
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
二、填空题(共8题;共24分)
1.在 ABCD中,若AB=3cm,AD=4cm,则它的周长为________cm.
2.已知一个菱形的两条对角线的长分别为5cm和8cm,该菱形的面积为________cm2 .
3.工人师博常常通过测量平行四边形零件的对角线是否相等来检验零件是否为矩形,请问工人师博此种检验方法依据的道理是________.
4.如图,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有________种.
5.如图,在四边形ABCD中,对角线AC、BD相交于点O,且AO=CO,BO=DO,要使四边形ABCD为矩形,则需添加的条件为________(填一个即可).
6如图,在四边形ABCD中,AB=BC=CD=DA , 对角线AC与BD相交于点O , 若不增加任何字母与辅助线,要使四边形ABCD是正方形,则还需增加一个条件是________?
7.如图,在平行四边形ABCD中,∠A与∠B的度数之比为2:1,则∠A=________°
8.如图,直线过正方形ABCD的顶点B,点A、C到直E的距离分别是1和2,则正方形ABCD面积是________.
三、解答题(共44分)
1.在四边形ABCD中,对角线AC、BD交于点O,若AD=12,OD=OB=5,AC=26,∠ADB=90?,求证:四边形ABCD为平行四边形.
2.如图,在△ABC中,AB=AC,D为BC边的中点,以AB、BD为邻边作?ABDE,连接AD,EC.求证:四边形ADCE是矩形.
3.如图,在△ABC中,AB=BC,D、E、F分别是BC、AC、AB边上的中点.
(1)求证:四边形BDEF是菱形;
(2)若AB=12cm,求菱形BDEF的周长。
4.如图,正方形ABCD中,E,F分别在AD,DC上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;
(1)求证:∠ABE= ∠BGE;
(3)若AB=4,AE=1,求S△BEG 。
5.如图,已知: , , ,
(1)图中有几个平行四边形?将它们分别表示出来。
(2)在(1)中选择一个进行证明。
(3)证明: 是 边上的中点。
答案
一、1—8 DDCBB BCC
二、
1. 14
2. 20
3. 对角线相等的平行四边形是矩形
4. 4
5. ∠DAB=90°
6. AC=BD或AB⊥BC(答案不唯一)
7. 120
8. 5
三、1. 证明:∵AD=12,OD=5,∠ADB=90°,
∴AO=13,
∵AC=26,
∴AO=OC=13,且DO=OB=5,
∴四边形ABCD为平行四边形
2.证明:∵AB=AC,D为BC边的中点,
∴AD⊥BC,BD=CD,
∴∠ADC=90°,
∵四边形ABDE是平行四边形,
∴AE∥BD,AE=BD,
∴AE∥CD,AE=CD,
∴四边形ADCE是平行四边形,
又∵∠ADC=90°,
∴四边形ADCE是矩形
3. (1)证明:∵D、E、F分别是BC、AC、AB的中点,
∴DE∥AB,EF∥BC,
∴四边形BDEF是平行四边形,
又∵DE= AB,EF= BC,且AB=BC,
∴DE=EF,
∴四边形BDEF是菱形;
(2)解:∵AB=12cm,F为AB中点,
∴BF=6cm,
∴菱形BDEF的周长为6×4=24cm.
4. (1)解:作GM⊥BE于M.
∵四边形ABCD是正方形,
∴AB=BC=4,∠A=∠ABC=∠BMG=90°,AD∥BG,
∵∠AEB=∠BEG,∠AEB=∠EBG,
∴∠BEG=∠EBG,
∴GE=GB,∵GM⊥EB,
∴∠MGB=∠MBE,BM=EM,
∵∠ABE+∠EBG=90°,∠EBG+∠MGB=90°,
∴∠ABE=∠MGB= ∠EGB
(2)解:在Rt△ABE中,BE= = = ,∴BM= ,
∵∠ABE=∠MGB,∠A=∠GMB=90°,
∴△ABE∽△MGB,
∴ = ,
∴ = ,
∴GM=2 ,
∴S△EBG= × ×2 =17.
5 (1)解:∵AB∥DF,ED∥BC,EF∥AC,
∴图中共有3个平行四边形,即 、 、 ;
(2)解:∵AB∥DF,EF∥AC,
∴AE∥DF,EF∥AD,
∴四边形AEFD是平行四边形.
(3)证明:四边形 和四边形 都是平行四边形,
?
?
是 边上的中点.
