人教版数学七年级下册 5.3.1平行线的性质 课件(19张)
文档属性
| 名称 | 人教版数学七年级下册 5.3.1平行线的性质 课件(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-05 09:31:53 | ||
图片预览


文档简介
(共19张PPT)
5.3.1平行线的性质
b
1
2
a
c
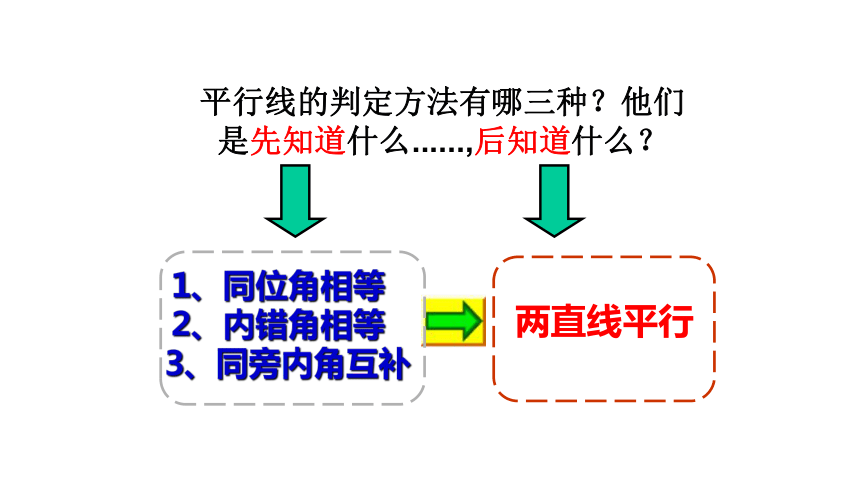
如图,
(1)∵ ∠1=____(已知)
∴ a ∥ b ( )
(2)∵ ∠3=____ (已知)
∴ a ∥ b (? )
(3)∵____ +∠3= 180 ° (已知)
∴ a ∥ b ( ??? )
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
c
a
b
1
5
3
4
你会吗?
2
6
∠5
∠5
∠6
两直线平行
1、同位角相等
2、内错角相等
3、同旁内角互补
平行线的判定方法有哪三种?他们是先知道什么......,后知道什么?
利用同位角相等,或者内错角相等,或者同旁内角互补可以判定两条直线平行.反过来如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
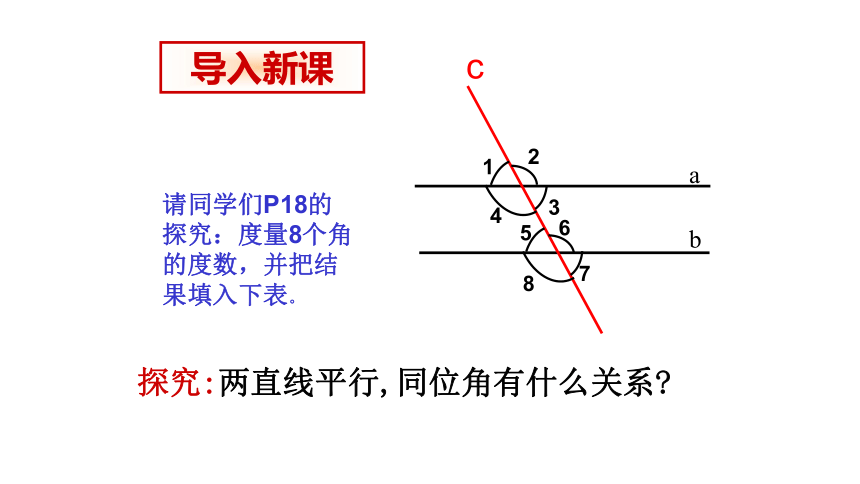
探究:两直线平行,同位角有什么关系?
a
b
c
1
5
2
3
4
7
6
8
请同学们P18的探究:度量8个角的度数,并把结果填入下表。
导入新课
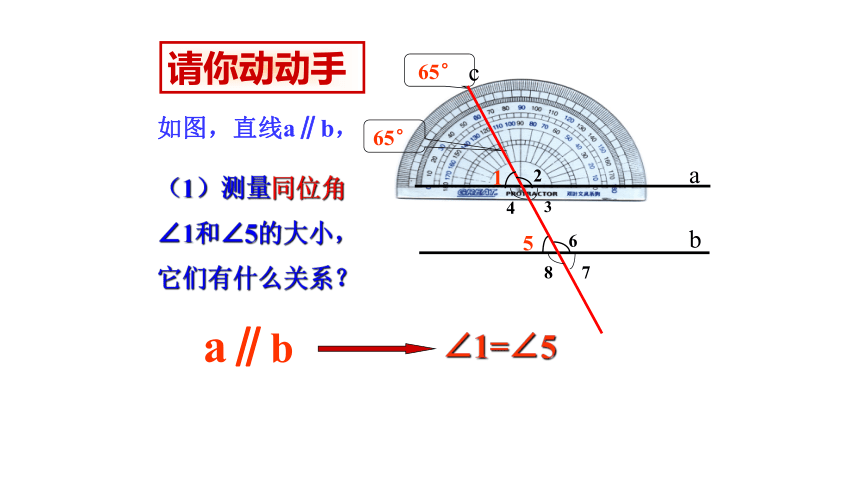
如图,直线a∥b,
(1)测量同位角∠1和∠5的大小,它们有什么关系?
65°
65°
c
a
b
1
5
2
4
3
6
8
7
∠1=∠5
a∥b
请你动动手
1
b
5
6
7
a
c
2
4
3
8
1
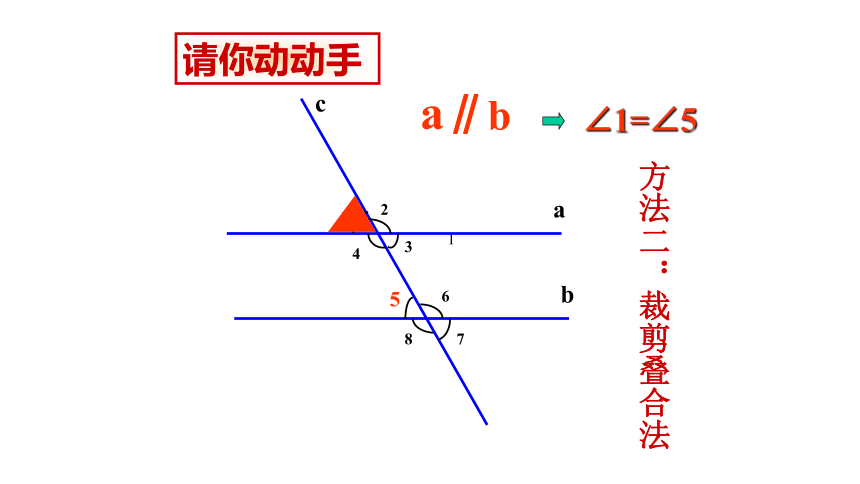
∠1=∠5
a∥b
方法二:裁剪叠合法
请你动动手
简单地说:两直线平行,同位角相等.
a
b
1
2
3
4
几何语言表述:
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
两条平行线被第三条直线所截,同位角相等.
平行线性质1:
得出结论
两直线平行,同位角相等.
几何语言表述:
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
a
b
1
2
3
4
猜想:两直线平行,内错角、同旁内角有怎么关系呢?相互讨论一下.
得出结论
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
平行线的性质:
a
b
1
2
3
4
得出结论
利用性质1来说明性质2和性质3
a
b
1
2
3
4
已知: a ∥ b ,
请说明∠2=∠3.
∵ a ∥ b (已知)
∴∠1=∠2( )
∵ ∠1=∠3( )
∴∠2=∠3 ( )
两直线平行,同位角相等
对顶角相等
等量代换
推 导
如图,
(1)∵ a ∥ b (已知)
∴ ∠1__∠2 ( )
(2)∵ a ∥ b (已知)
∴ ∠2____∠3 (? )
(3)∵ a ∥ b (已知)
∴ ∠2+∠4=_ ___ ( ??? )
=
两直线平行, 同位角相等
=
两直线平行,内错角相等
180 °
两直线平行,同旁内角互补
c
a
b
1
2
3
4
书写格式
两直线平行
同位角相等
内错角相等
同旁内角互补
线的关系
角的关系
判定
性质
平行线的“判定”与“性质”有什么不同?
1、如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度?为什么?
(2)从∠1=110o可以知道 ∠3是多少度?为什么?
(3)从 ∠1=110 o可以知道∠4 是多少度?为什么?
2
E
1
3
4
A
B
D
C
∠2=110o
∵两直线行,内错角相等
∠3=110o
∵两直线平行,同位角相等
∠4=70o
∵两直线平行,同旁内角互补
一、快速抢答
2、如图 ∵AD ∥BC,
∴∠1=∠2 (两直线平行,同位角角相等 )( )
二、是是非非
A
B
C
D
1
2
×
3、如果有两条直线被第三条直线所截,
那么必定有 ( )
A、内错角相等 B、同位角相等
C、同旁内角互补 D、以上都不对.
三、选选看
D
解:
∵AB∥CD
(已知)
∴∠B=∠C
两直线平行,内错角相等
又∵∠B=142°
∴ ∠C= ∠B=142°( )
(已知)
等量代换
C
B
A
D
4.如图,已知AB//CD, ∠B =142°,求∠C
(
)
四、填填看
图形
已知
结果
依据
同位角
内错角
同旁内角
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
平行线的性质
六、小结
发现数学结论的方法:
1.数学实验(测量、叠合等)法
2.猜想、推理法
5.3.1平行线的性质
b
1
2
a
c
如图,
(1)∵ ∠1=____(已知)
∴ a ∥ b ( )
(2)∵ ∠3=____ (已知)
∴ a ∥ b (? )
(3)∵____ +∠3= 180 ° (已知)
∴ a ∥ b ( ??? )
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
c
a
b
1
5
3
4
你会吗?
2
6
∠5
∠5
∠6
两直线平行
1、同位角相等
2、内错角相等
3、同旁内角互补
平行线的判定方法有哪三种?他们是先知道什么......,后知道什么?
利用同位角相等,或者内错角相等,或者同旁内角互补可以判定两条直线平行.反过来如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
探究:两直线平行,同位角有什么关系?
a
b
c
1
5
2
3
4
7
6
8
请同学们P18的探究:度量8个角的度数,并把结果填入下表。
导入新课
如图,直线a∥b,
(1)测量同位角∠1和∠5的大小,它们有什么关系?
65°
65°
c
a
b
1
5
2
4
3
6
8
7
∠1=∠5
a∥b
请你动动手
1
b
5
6
7
a
c
2
4
3
8
1
∠1=∠5
a∥b
方法二:裁剪叠合法
请你动动手
简单地说:两直线平行,同位角相等.
a
b
1
2
3
4
几何语言表述:
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
两条平行线被第三条直线所截,同位角相等.
平行线性质1:
得出结论
两直线平行,同位角相等.
几何语言表述:
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
a
b
1
2
3
4
猜想:两直线平行,内错角、同旁内角有怎么关系呢?相互讨论一下.
得出结论
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
平行线的性质:
a
b
1
2
3
4
得出结论
利用性质1来说明性质2和性质3
a
b
1
2
3
4
已知: a ∥ b ,
请说明∠2=∠3.
∵ a ∥ b (已知)
∴∠1=∠2( )
∵ ∠1=∠3( )
∴∠2=∠3 ( )
两直线平行,同位角相等
对顶角相等
等量代换
推 导
如图,
(1)∵ a ∥ b (已知)
∴ ∠1__∠2 ( )
(2)∵ a ∥ b (已知)
∴ ∠2____∠3 (? )
(3)∵ a ∥ b (已知)
∴ ∠2+∠4=_ ___ ( ??? )
=
两直线平行, 同位角相等
=
两直线平行,内错角相等
180 °
两直线平行,同旁内角互补
c
a
b
1
2
3
4
书写格式
两直线平行
同位角相等
内错角相等
同旁内角互补
线的关系
角的关系
判定
性质
平行线的“判定”与“性质”有什么不同?
1、如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度?为什么?
(2)从∠1=110o可以知道 ∠3是多少度?为什么?
(3)从 ∠1=110 o可以知道∠4 是多少度?为什么?
2
E
1
3
4
A
B
D
C
∠2=110o
∵两直线行,内错角相等
∠3=110o
∵两直线平行,同位角相等
∠4=70o
∵两直线平行,同旁内角互补
一、快速抢答
2、如图 ∵AD ∥BC,
∴∠1=∠2 (两直线平行,同位角角相等 )( )
二、是是非非
A
B
C
D
1
2
×
3、如果有两条直线被第三条直线所截,
那么必定有 ( )
A、内错角相等 B、同位角相等
C、同旁内角互补 D、以上都不对.
三、选选看
D
解:
∵AB∥CD
(已知)
∴∠B=∠C
两直线平行,内错角相等
又∵∠B=142°
∴ ∠C= ∠B=142°( )
(已知)
等量代换
C
B
A
D
4.如图,已知AB//CD, ∠B =142°,求∠C
(
)
四、填填看
图形
已知
结果
依据
同位角
内错角
同旁内角
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
平行线的性质
六、小结
发现数学结论的方法:
1.数学实验(测量、叠合等)法
2.猜想、推理法
