人教版数学七年级下册5.2.2平行线的判定 课件(37张)
文档属性
| 名称 | 人教版数学七年级下册5.2.2平行线的判定 课件(37张) |

|
|
| 格式 | zip | ||
| 文件大小 | 379.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-05 00:00:00 | ||
图片预览






文档简介
(共37张PPT)
平行线的判定
学习目标
1、掌握平行线的三种判定方法。并会运
用所学方法来判断两条直线是否平行。
2、会根据判定方法进行简单的推理并学
会用数学符号写出简单的推理过程。
3、体会数学中的转化思想。
重点:1.了解平行线的定义,并能用符号表示.能借助三角板,方格纸等画平行线.
2.探索平行线的基本性质(基本事实).
难点:探索平行线的基本判定方法
复习提问
(1)平面内两条直线的位置关系有几种?
(2)怎样过已知直线外一点画已知直线的平行线?
相交与平行
1
注意观察!
a
b
.
P
2
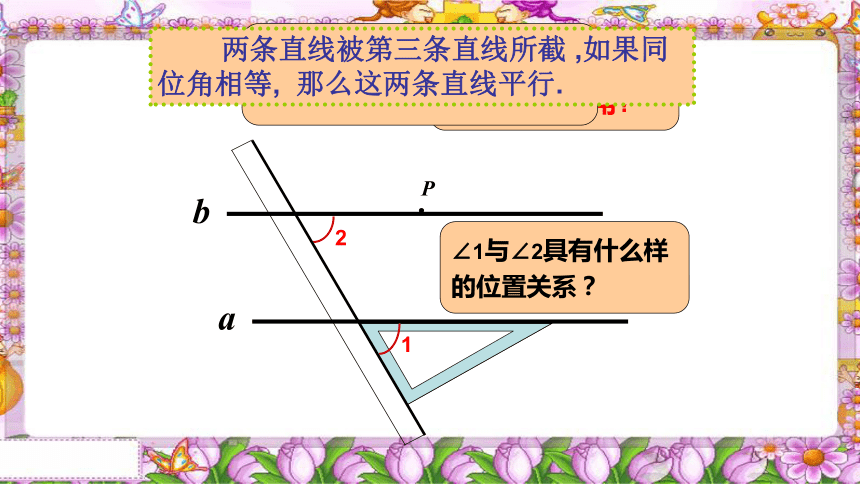
如何画平行线?
刚才的画法中,三角板起着什么作用?
想一想!
∠1与∠2具有什么样的位置关系?
我们能得到一个判定两直线平行的方法吗?
两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行.
两条直线被第三条直线所截 ,如
果同位角相等, 那么这两条直线平行.
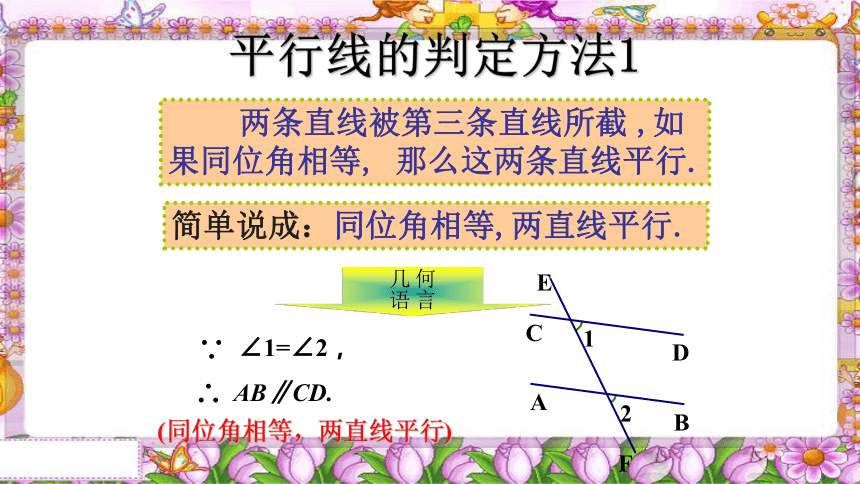
平行线的判定方法1
简单说成:同位角相等,两直线平行.
何言
几语
(同位角相等,两直线平行)
?
∠1=∠2,
?
AB∥CD.
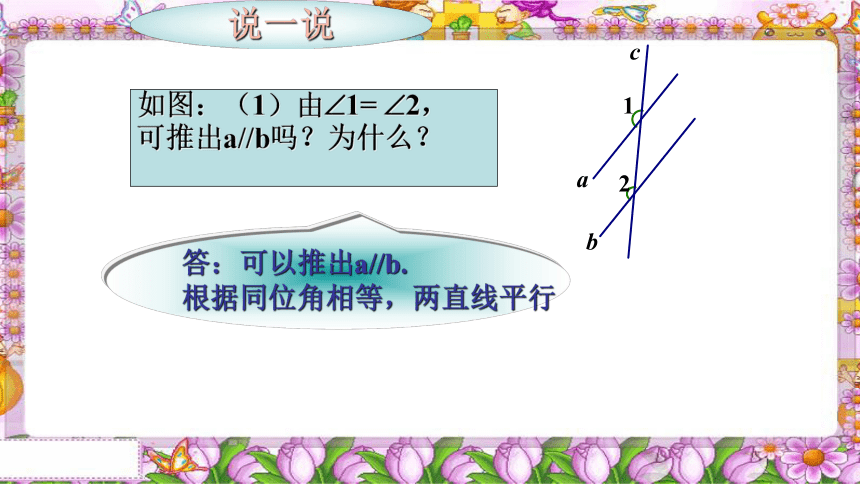
如图:(1)由?1= ?2,
可推出a//b吗?为什么?
说一说
答:可以推出a//b.
根据同位角相等,两直线平行
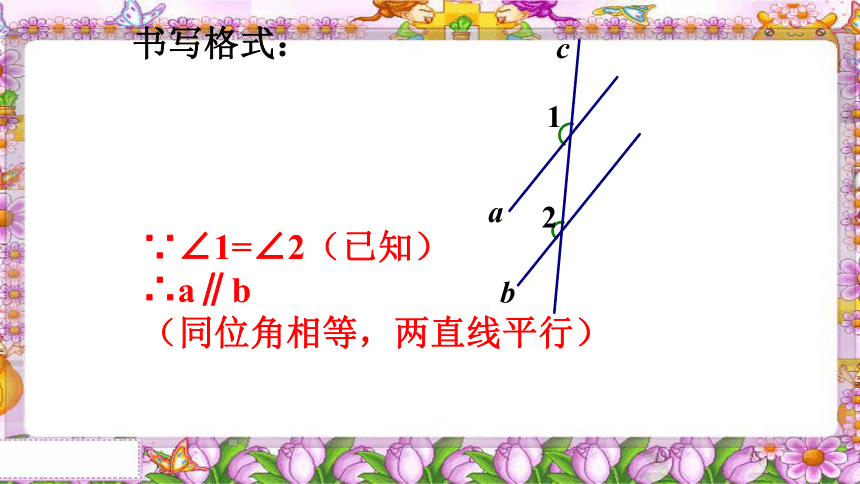
∵∠1=∠2(已知)
∴a∥b
(同位角相等,两直线平行)
书写格式:
1.如图,哪两个角相等能判定直线AB∥CD?
D
B
4
3
1
4
3
2
A
C
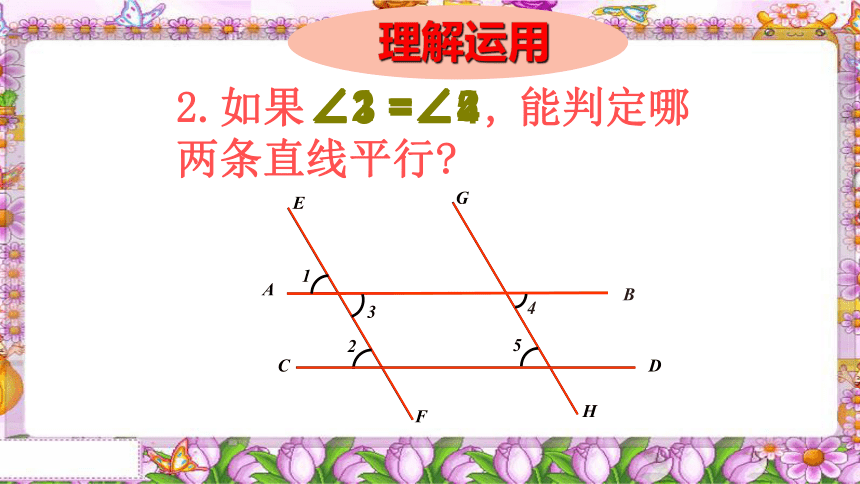
理解运用
2.如果 , 能判定哪两条直线平行?
∠1 =∠2
A
B
C
E
F
D
2
5
H
G
4
1
3
∠3 =∠4
∠2 =∠5
理解运用
如图,已知∠1=∠2,AB与CD平行吗?为什么?
探究1
A
B
C
D
E
F
1
2
3
?
∠1 =∠2(已知),
∠2 =∠3(对顶角相等),
?
∠1 =∠3.
?
AB∥CD
(同位角相等,两直线平行).
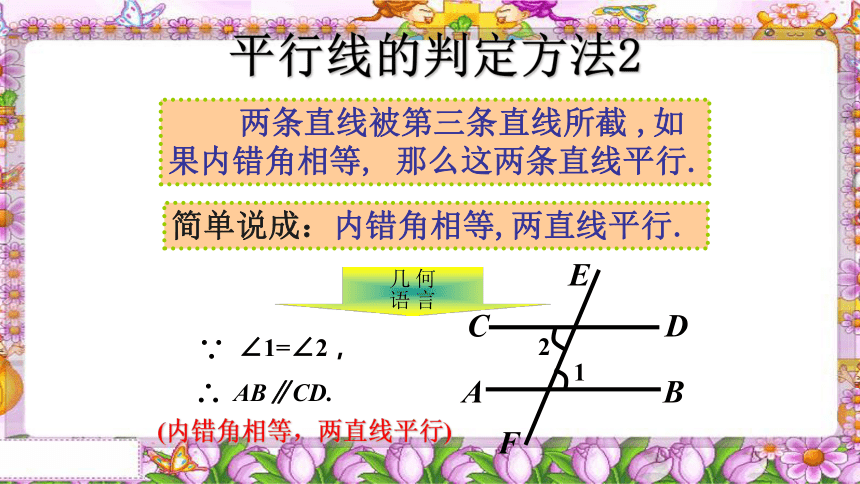
两条直线被第三条直线所截 ,如
果内错角相等, 那么这两条直线平行.
平行线的判定方法2
简单说成:内错角相等,两直线平行.
何言
几语
(内错角相等,两直线平行)
A
B
C
D
E
F
1
2
?
∠1=∠2,
?
AB∥CD.
如图,∠1= ∠2 ,且∠1=∠3, AB和CD平行吗?
A
B
C
D
1
2
3
想一想
练一练
练习:已知:∠1=∠A=∠C,
(1)从∠1=∠A,可以判断哪两条直线平行?它的依据是什么?
(2)从∠1=∠C,可以判断哪两条直线平行?它的依据是什么?
如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?
A
B
C
D
E
F
1
2
?
∠1 +∠2=180°(已知),
∠2 +∠3=180°(邻补角互补),
?
∠1 =∠3(同角的补角相等).
?
AB∥CD
(内错角相等,两直线平行).
探究2
3
如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?
A
B
C
D
E
F
1
3
2
?
∠1 +∠2=180°(已知),
∠2 +∠3=180°(邻补角互补),
?
∠1 =∠3(同角的补角相等).
?
AB∥CD
(同位角相等,两直线平行).
探究2
两条直线被第三条直线所截 ,如
果同旁内角互补, 那么这两条直线平行.
平行线的判定方法3
简单说成:同旁内角互补,两直线平行.
何言
几语
(同旁内角互补,两直线平行)
A
B
C
D
E
F
1
2
?
∠1+∠2=180°,
?
AB∥CD.
如图:?B= ? D=45°, ? C=135°,
问图中有哪些直线平行?
答:AB//CD,AD//BC
∵? B=45°(已知)
? C=135°(已知)
?? B+ ? C=180°
? AB//CD(同旁内角互补,两直线平行)
同理:AD//BC
D
C
B
A
想一想
判定两条直线平行的方法
文字叙述 符号语言 图形
相等
两直线平行 ∵ (已知)
∴a∥b
相等
两直线平行 ∵ (已知)
∴a∥b
互补,两直线平行 ∵
∴a∥b
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
3
4
例题1.
① ∵ ∠1 =_____ (已知)
∴ AB∥CE
② ∵ ∠2 = (已知)
∴ CD∥BF
③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____
AB
CE
∠2
∠4
如图:
1
3
5
4
2
C
F
E
A
D
B
(内错角相等,两直线平行)
(同位角相等,两直线平行)
(同旁内角互补,两直线平行)
已知∠3=45 °,∠1与∠2互余,你能得到 ?
解∵∠1+∠2=90° ∠1=∠2
∴∠1=∠2=45°
∵ ∠3=45°
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)
1
2
3
A
B
C
D
AB//CD
例题2
应用练习
1.如图,如果∠3=∠7,那么 _____∥_____,理由是__________ ;如果∠5=∠3,那么_____∥_____,理由是__________ ;如果∠2+∠5= ______°,那么 ∥ ,理由是__________ .
a
b
a
b
同位角相等,两直线平行
内错角相等,两直线平行
180
a
b
同旁内角互补,两直线平行
2、如图,∠1=∠2,则下列结论正确的是( )
(A)AD//BC (B)AB//CD
(C)AD//EF (D)EF//BC
C
应用练习
应用练习
3.如图所示,直线 , 被直线 所截,现给 出下列四个条件:①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明
∥ 的条件序号为( )
A.①② B.①③ C.①④ D.③④
a
b
c
a
b
A
4、如图,哪些直线平行,哪些直线不平行?
与 平行, 与 不平行
应用练习
5.如图:可以确定AB∥CE的条件是( )
A.∠2=∠B
B. ∠1=∠A
C. ∠3=∠B
D. ∠3=∠A
A E
B C D
1
2
3
C
应用练习
6.如图,已知∠1=30°,∠2或 ∠3
满足条件___________,则a//b
2
1
3
a
b
c
∠2=150 或∠3=30°
__________
//
.
180
7
6
)
4
(
;
1
4
)
3
(
;
6
3
)
2
(
;
2
1
)
1
(
0
的条件序号是
其中能识别
所截,给出下列条件:
被直线
、
7.直线
b
a
c
b
a
=
?
+
?
?
=
?
?
=
?
?
=
?
(1)(2)(4)
4
8
6
2
1
5
3
7
a
b
c
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定示意图
判定
数量关系
位置关系
小结
(1)从∠1=∠2,可以推出 ∥ ,
理由是 。
(2)从∠2=∠ ,可以推出c∥d ,
理由是 。
(3)如果∠1=75°,∠4=105°,
可以推出 ∥ 。
理由是 。
练一练
b
a
内错角相等,两直线平行
同位角相等,两直线平行
3
a
b
4
2
c
d
3
1
a
b
同旁内角互补,两直线平行
1.如图
从∠1=∠4,可以推出 ∥ ,
理由是 。
(2)从∠ABC +∠ =180,可以推出AB∥CD ,
理由是 。
(3)从∠ =∠ ,可以推出AD∥BC,
理由是 。
A
B
C
D
1
2
3
4
5
(4)从∠5=∠ ,可以推出AB∥CD,
理由是 。
练一练
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
2
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
2.如图
如图,∠1=∠2,能判断AB∥DF吗?为什么?
若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由。
?
?
?
?
?
?
F
D
C
A
B
E
1
2
思考
不能.
添加∠CBD=∠EDB
内错角相等,两直线平行
想想还可以添加什么条件?
2、直线a、b与直线c相交,给出下列条件:
①∠1= ∠2②∠3= ∠6③∠4+∠7=1800
④∠3+ ∠5=1800,其中能判断a//b的是
( )
A ①②③④ B ①③④ C ①③ D ④
6
4
1
5
7
3
2
8
a
b
B
∠ C=61
当∠ABE= 度时,EF∥CN
当∠CBF= 度时,EF∥CN
。
3、如图
A
B
C
N
E
F
必做题:
1、如果∠A +∠B =180°,那么根据同旁内
角互补,两直线平行,可得_____∥_____;
如果 +∠B =180°,那么根据同旁内角
互补,两直线平行,可得AB∥EC。
A
B
C
E
AE BC
61
61
∠C
终极挑战
1.下列说法错误的是( )
A.同位角不一定相等 B.内错角都相等
C.同旁内角互补 D.同位角相等,两直线平行。
2. .如图所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF
3.在同一平面内,若直线a,b,c满足a⊥b,a⊥c,则b与c的位置关系是______.
第2题
D
D
b∥c
4.如图1所示,下列条件中,能判断AB∥CD的是( )
A.∠BAD=∠BCD B.∠1=∠2; C.∠3=∠4 D.∠BAC=∠ACD
(1) (2)
5.如图2所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF
6.如图3所示,能判断AB∥CE的条件是( )
A.∠A=∠ACE B.∠A=∠ECD C.∠B=∠BCA D.∠B=∠ACE
(3)
7.下列说法错误的是( )
A.同位角不一定相等 B.内错角都相等
C.同旁内角可能相等 D.同旁内角互补,两直线平行
8.不相邻的两个直角,如果它们有一边在同一直线上,那么另一边相互( )
A.平行 B.垂直 C.平行或垂直 D.平行或垂直或相交
9.如图,根据下列条件可判断哪两条直线平行,并说明理由。
(1)∠1=∠2 (2)∠3=∠A
(3)∠A+∠2+∠4=180°
终极挑战
平行线的判定
学习目标
1、掌握平行线的三种判定方法。并会运
用所学方法来判断两条直线是否平行。
2、会根据判定方法进行简单的推理并学
会用数学符号写出简单的推理过程。
3、体会数学中的转化思想。
重点:1.了解平行线的定义,并能用符号表示.能借助三角板,方格纸等画平行线.
2.探索平行线的基本性质(基本事实).
难点:探索平行线的基本判定方法
复习提问
(1)平面内两条直线的位置关系有几种?
(2)怎样过已知直线外一点画已知直线的平行线?
相交与平行
1
注意观察!
a
b
.
P
2
如何画平行线?
刚才的画法中,三角板起着什么作用?
想一想!
∠1与∠2具有什么样的位置关系?
我们能得到一个判定两直线平行的方法吗?
两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行.
两条直线被第三条直线所截 ,如
果同位角相等, 那么这两条直线平行.
平行线的判定方法1
简单说成:同位角相等,两直线平行.
何言
几语
(同位角相等,两直线平行)
?
∠1=∠2,
?
AB∥CD.
如图:(1)由?1= ?2,
可推出a//b吗?为什么?
说一说
答:可以推出a//b.
根据同位角相等,两直线平行
∵∠1=∠2(已知)
∴a∥b
(同位角相等,两直线平行)
书写格式:
1.如图,哪两个角相等能判定直线AB∥CD?
D
B
4
3
1
4
3
2
A
C
理解运用
2.如果 , 能判定哪两条直线平行?
∠1 =∠2
A
B
C
E
F
D
2
5
H
G
4
1
3
∠3 =∠4
∠2 =∠5
理解运用
如图,已知∠1=∠2,AB与CD平行吗?为什么?
探究1
A
B
C
D
E
F
1
2
3
?
∠1 =∠2(已知),
∠2 =∠3(对顶角相等),
?
∠1 =∠3.
?
AB∥CD
(同位角相等,两直线平行).
两条直线被第三条直线所截 ,如
果内错角相等, 那么这两条直线平行.
平行线的判定方法2
简单说成:内错角相等,两直线平行.
何言
几语
(内错角相等,两直线平行)
A
B
C
D
E
F
1
2
?
∠1=∠2,
?
AB∥CD.
如图,∠1= ∠2 ,且∠1=∠3, AB和CD平行吗?
A
B
C
D
1
2
3
想一想
练一练
练习:已知:∠1=∠A=∠C,
(1)从∠1=∠A,可以判断哪两条直线平行?它的依据是什么?
(2)从∠1=∠C,可以判断哪两条直线平行?它的依据是什么?
如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?
A
B
C
D
E
F
1
2
?
∠1 +∠2=180°(已知),
∠2 +∠3=180°(邻补角互补),
?
∠1 =∠3(同角的补角相等).
?
AB∥CD
(内错角相等,两直线平行).
探究2
3
如图,已知∠1+∠2=180°,AB与CD平行吗?为什么?
A
B
C
D
E
F
1
3
2
?
∠1 +∠2=180°(已知),
∠2 +∠3=180°(邻补角互补),
?
∠1 =∠3(同角的补角相等).
?
AB∥CD
(同位角相等,两直线平行).
探究2
两条直线被第三条直线所截 ,如
果同旁内角互补, 那么这两条直线平行.
平行线的判定方法3
简单说成:同旁内角互补,两直线平行.
何言
几语
(同旁内角互补,两直线平行)
A
B
C
D
E
F
1
2
?
∠1+∠2=180°,
?
AB∥CD.
如图:?B= ? D=45°, ? C=135°,
问图中有哪些直线平行?
答:AB//CD,AD//BC
∵? B=45°(已知)
? C=135°(已知)
?? B+ ? C=180°
? AB//CD(同旁内角互补,两直线平行)
同理:AD//BC
D
C
B
A
想一想
判定两条直线平行的方法
文字叙述 符号语言 图形
相等
两直线平行 ∵ (已知)
∴a∥b
相等
两直线平行 ∵ (已知)
∴a∥b
互补,两直线平行 ∵
∴a∥b
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
3
4
例题1.
① ∵ ∠1 =_____ (已知)
∴ AB∥CE
② ∵ ∠2 = (已知)
∴ CD∥BF
③ ∵ ∠1 +∠5 =180o(已知)
∴ _____∥_____
AB
CE
∠2
∠4
如图:
1
3
5
4
2
C
F
E
A
D
B
(内错角相等,两直线平行)
(同位角相等,两直线平行)
(同旁内角互补,两直线平行)
已知∠3=45 °,∠1与∠2互余,你能得到 ?
解∵∠1+∠2=90° ∠1=∠2
∴∠1=∠2=45°
∵ ∠3=45°
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)
1
2
3
A
B
C
D
AB//CD
例题2
应用练习
1.如图,如果∠3=∠7,那么 _____∥_____,理由是__________ ;如果∠5=∠3,那么_____∥_____,理由是__________ ;如果∠2+∠5= ______°,那么 ∥ ,理由是__________ .
a
b
a
b
同位角相等,两直线平行
内错角相等,两直线平行
180
a
b
同旁内角互补,两直线平行
2、如图,∠1=∠2,则下列结论正确的是( )
(A)AD//BC (B)AB//CD
(C)AD//EF (D)EF//BC
C
应用练习
应用练习
3.如图所示,直线 , 被直线 所截,现给 出下列四个条件:①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能说明
∥ 的条件序号为( )
A.①② B.①③ C.①④ D.③④
a
b
c
a
b
A
4、如图,哪些直线平行,哪些直线不平行?
与 平行, 与 不平行
应用练习
5.如图:可以确定AB∥CE的条件是( )
A.∠2=∠B
B. ∠1=∠A
C. ∠3=∠B
D. ∠3=∠A
A E
B C D
1
2
3
C
应用练习
6.如图,已知∠1=30°,∠2或 ∠3
满足条件___________,则a//b
2
1
3
a
b
c
∠2=150 或∠3=30°
__________
//
.
180
7
6
)
4
(
;
1
4
)
3
(
;
6
3
)
2
(
;
2
1
)
1
(
0
的条件序号是
其中能识别
所截,给出下列条件:
被直线
、
7.直线
b
a
c
b
a
=
?
+
?
?
=
?
?
=
?
?
=
?
(1)(2)(4)
4
8
6
2
1
5
3
7
a
b
c
同位角相等
内错角相等
同旁内角互补
两直线平行
平行线的判定示意图
判定
数量关系
位置关系
小结
(1)从∠1=∠2,可以推出 ∥ ,
理由是 。
(2)从∠2=∠ ,可以推出c∥d ,
理由是 。
(3)如果∠1=75°,∠4=105°,
可以推出 ∥ 。
理由是 。
练一练
b
a
内错角相等,两直线平行
同位角相等,两直线平行
3
a
b
4
2
c
d
3
1
a
b
同旁内角互补,两直线平行
1.如图
从∠1=∠4,可以推出 ∥ ,
理由是 。
(2)从∠ABC +∠ =180,可以推出AB∥CD ,
理由是 。
(3)从∠ =∠ ,可以推出AD∥BC,
理由是 。
A
B
C
D
1
2
3
4
5
(4)从∠5=∠ ,可以推出AB∥CD,
理由是 。
练一练
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
2
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
2.如图
如图,∠1=∠2,能判断AB∥DF吗?为什么?
若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由。
?
?
?
?
?
?
F
D
C
A
B
E
1
2
思考
不能.
添加∠CBD=∠EDB
内错角相等,两直线平行
想想还可以添加什么条件?
2、直线a、b与直线c相交,给出下列条件:
①∠1= ∠2②∠3= ∠6③∠4+∠7=1800
④∠3+ ∠5=1800,其中能判断a//b的是
( )
A ①②③④ B ①③④ C ①③ D ④
6
4
1
5
7
3
2
8
a
b
B
∠ C=61
当∠ABE= 度时,EF∥CN
当∠CBF= 度时,EF∥CN
。
3、如图
A
B
C
N
E
F
必做题:
1、如果∠A +∠B =180°,那么根据同旁内
角互补,两直线平行,可得_____∥_____;
如果 +∠B =180°,那么根据同旁内角
互补,两直线平行,可得AB∥EC。
A
B
C
E
AE BC
61
61
∠C
终极挑战
1.下列说法错误的是( )
A.同位角不一定相等 B.内错角都相等
C.同旁内角互补 D.同位角相等,两直线平行。
2. .如图所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF
3.在同一平面内,若直线a,b,c满足a⊥b,a⊥c,则b与c的位置关系是______.
第2题
D
D
b∥c
4.如图1所示,下列条件中,能判断AB∥CD的是( )
A.∠BAD=∠BCD B.∠1=∠2; C.∠3=∠4 D.∠BAC=∠ACD
(1) (2)
5.如图2所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF
6.如图3所示,能判断AB∥CE的条件是( )
A.∠A=∠ACE B.∠A=∠ECD C.∠B=∠BCA D.∠B=∠ACE
(3)
7.下列说法错误的是( )
A.同位角不一定相等 B.内错角都相等
C.同旁内角可能相等 D.同旁内角互补,两直线平行
8.不相邻的两个直角,如果它们有一边在同一直线上,那么另一边相互( )
A.平行 B.垂直 C.平行或垂直 D.平行或垂直或相交
9.如图,根据下列条件可判断哪两条直线平行,并说明理由。
(1)∠1=∠2 (2)∠3=∠A
(3)∠A+∠2+∠4=180°
终极挑战
