人教版高一必修二5.1曲线运动课时2:运动的合成与分解(共35张PPT)
文档属性
| 名称 | 人教版高一必修二5.1曲线运动课时2:运动的合成与分解(共35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-05 09:27:24 | ||
图片预览









文档简介
(共35张PPT)
5.1曲线运动
运动的合成与分解
回顾巩固知识
1、曲线运动的特点?
2、曲线运动的条件?
合外力F方向与速度v方向不共线。
(夹角大小与速度大小)
3、外力F是否变化的影响?
(匀变速和变加速曲线)
4、曲线运动轨迹与力、速度的方向关系
V沿着轨迹上点的切线方向,
轨迹夹在F、V之间,
力F指向轨迹内侧,
轨迹偏向力F的方向
运动方向时刻在改变
变速运动,一定有加速度,
合外力不为零
轨迹是曲线
学习目标:
1.什么是合运动和分运动
2.什么是运动的合成和分解
3.分运动和合运动具有等时性
4.运动的合成和分解遵循平行四边形法则
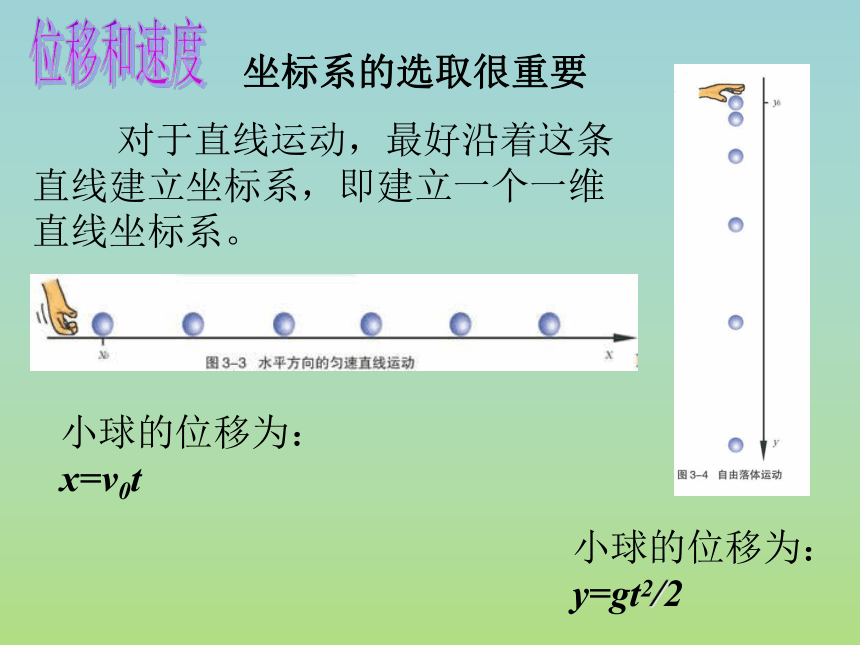
坐标系的选取很重要
对于直线运动,最好沿着这条直线建立坐标系,即建立一个一维直线坐标系。
小球的位移为: x=v0t
小球的位移为: y=gt2/2
以抛出点为坐标原点;初速度v0的方向为x 轴的正方向;竖直向下的方向为y 轴正方向
研究的问题是:
1、速度
2、位移
举例:水平抛出的小球的运动
v0
P(x,y)
O
y
x
s
θ
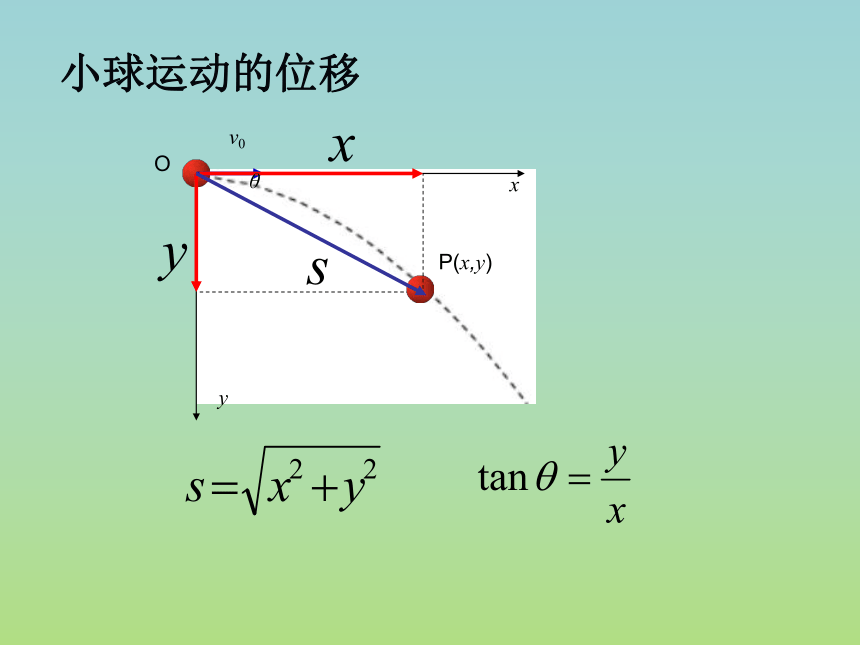
小球运动的位移
x
y
小球运动的速度
飞机起飞时以300km/h的速度斜向上飞,飞行方向与水平方面的夹角30o。求水平方向的分速度vx和竖直方向的分速度vy
请同学们思考并独立完成
例题1:书本第4页
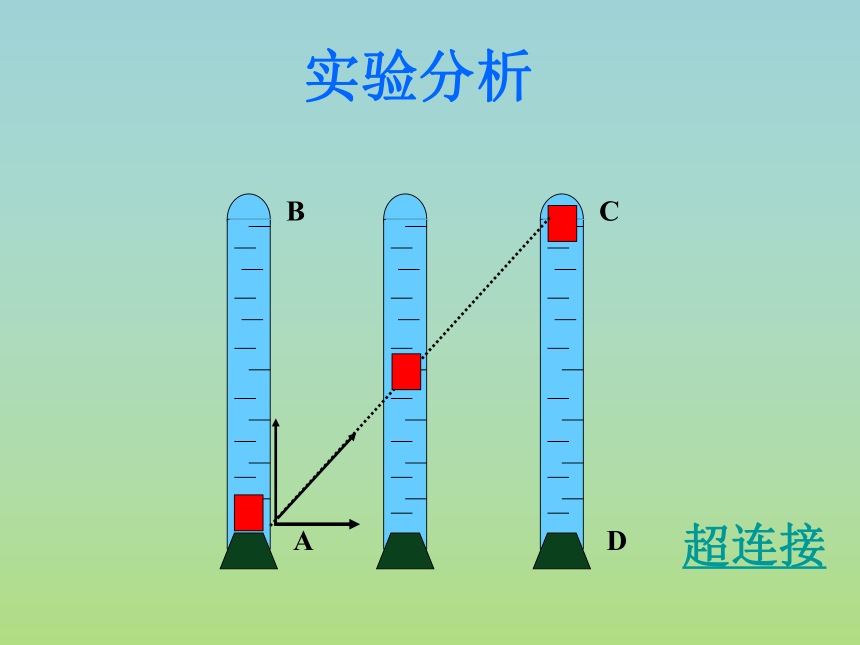
实验分析
实验装置
实验1
实验2
演示实验:阅读课本P5页演示实验
超连接
实验分析
实验分析:
实验1:红蜡块R沿玻璃管匀速上升,做直线运
动。红蜡块R由A到B,它的位移是AB。
实验2:红蜡块在上升的同时,玻璃管水平向
右匀速移动,红蜡块实际上是斜向右上
方运动的。红蜡块将沿直线AC到达C,
位移是AC。
红蜡块同时参与了两个运动:
1.在玻璃管中竖直向上的运动(由A到B)
2.随玻璃管水平向右的运动(由A到D)
结论:红蜡块实际发生的运动是这两个运动合成的结果
合运动和分运动
分运动:蜡块沿玻璃管在竖直方向的运动和随管做的水平方向的运动,叫做分运动。
合运动:蜡块实际发生的运动叫做合运动
合位移(速度、加速度):合运动的位移 ( 速度、加速度 )
分位移(速度、加速度):分运动的位移( 速度、 加速度)
等时性 各分运动与合运动同时发生和结束,时间相同
等效性 各分运动的共同效果与合运动的效果相同
同体性 各分运动与合运动是同一物体的运动
独立性 各分运动之间互不相干,彼此独立,互不影响
结论: 运动的合成和分解遵循平等四边形定则。
思考1:位移、速度、加速度是标量
还是矢量?
思考2:如何对位移、速度、加速度
进行合成和分解?
思考3:如何对运动进行合成和分解?
练习1:已知蜡块在水平方向的速度为Vx=4cm/s,在竖直方向的速度为Vy=3cm/s,求蜡块运动的速度。
已知分运动求合运动的过程——运动的合成
练习2:书本第7页第2题
练2拓展:跳伞员从高空自由下落,落地前的遇到水平方向吹来的风,则跳伞员在空中下落的时间与无风时比较将( )
A.增长 B.不变 C.缩短 D.无法确定
【解析】选B.根据运动的独立性可知,水滴在竖直方向上的运动和水平方向上的运动互不干涉,其下落时间仅取决于竖直下落的高度,因此选项B正确.
1)是直线运动还是曲线运动?(判断轨迹)
2)是匀变速运动还是变加速运动?(判断运动性质)
思考:如何判断两个直线运动的合运动的运动轨迹和运动性质?
合力F合的方向(或加速度a的方向)与合速度v合的方向是否同一直线
合力(或加速度)是否恒定
练习4.关于互成角度的两个初速度不为零的匀变速直线运动的合运动,下述说法正确的是( )
A.一定是直线运动 B.一定是曲线运动
C. 可能是直线运动,也可能是曲线运动 D.以上都不对
【解析】选C.两个运动的初速度合成、加速度合成如图所示.当a和v重合时,物体做直线运动;当a和v不重合时,物体做曲线运动.由于题目没有给出两个运动的加速度和初速度的具体数值,所以以上两种情况都有可能.选项C正确.
匀加速直线运动
加速曲线运动
画图分析两个加速运动的合成
(一定是匀速直线运动)
2、两互成角度的初速为零的匀加速直线运动的合成
(一定是匀加速直线运动)
3、两互成角度的初速不为零的匀加速直线运动的合成
(匀变速直线运动或匀变速曲线运动)
4、一个匀速直线运动和一个匀加速直线运动的合成
(匀变速直线运动或匀变速曲线运动)
1、两互成角度的匀速直线运动的合成
课堂训练
河宽d=100m,水流速度v1=3m/s,船在静水中的速度是v2=4m/s。求
(1)欲使船渡河时间最短,船应怎样渡河?最短时间是多少?船经过的位移多大?
(2)欲使船渡河距离最短,船应怎样渡河?渡河时间多长?
小船渡河
在流动的河水中渡河的轮船的运动可分解为两个运动:
假设轮船不开动,轮船随水流一起向下游运动;
假设河水不流动,轮船相对河水的运动。
分析1:航程最短
θ
d
分析小船的运动
(1)如果要求船划到对岸航程最短,则船头应指向什么方向?最短航程是多少?所用时间多少?
v水
v合
v船
d
θ
总结:渡河的最短位移大小就是河宽,但是实现这一最短位移,必须满足船在静水的速度大于河水的速度。
分析2:时间最短
d
(2)如果要求船划到对岸时间最短,则船头应指向什么方向?最短时间是多少?航程是多少?
d
θ
A
B
C
总结、渡河的时间最短则船头指向必须和河岸垂直,不受河水速度大小的影响。
v水
v合
v船
上题中,如果水速V水=3m/s,船在静水中的速度V船=4m/s,结果如何呢?
如果河水的速度大于船在静水的速度时,这时船不可能垂直渡河,但仍存在最短位移,求解的方法如下:
d
θ
V合
V水
V船
②渡河的最短位移
v船 < v水的情况
v水
smin
D
O
A
v
小船渡河问题
v船
B
上游
下游
在高处拉低处小船时,通常在河岸上通过滑轮用钢绳拴船,若拉绳的速度为4m/s,当拴船的绳与水平方向成60°时,船的速度是多少?
提示:将船的运动分解成沿绳方向的运动和垂直绳方向的运动。
课堂练习
小结
一、合运动和分运动
1、概念:如果物体同时参与了几个运动,那么物体实际发生的运动就叫做那几个运动的合运动,那几个运动叫做这个实际运动的分运动。
2、合运动和分运动的关系
等效性、独立性、等时性
二、运动的合成和分解
1、遵循平行四边形法则
2、两个直线运动的合成可以是直线运动,也可以是曲线运动。
5.1曲线运动
运动的合成与分解
回顾巩固知识
1、曲线运动的特点?
2、曲线运动的条件?
合外力F方向与速度v方向不共线。
(夹角大小与速度大小)
3、外力F是否变化的影响?
(匀变速和变加速曲线)
4、曲线运动轨迹与力、速度的方向关系
V沿着轨迹上点的切线方向,
轨迹夹在F、V之间,
力F指向轨迹内侧,
轨迹偏向力F的方向
运动方向时刻在改变
变速运动,一定有加速度,
合外力不为零
轨迹是曲线
学习目标:
1.什么是合运动和分运动
2.什么是运动的合成和分解
3.分运动和合运动具有等时性
4.运动的合成和分解遵循平行四边形法则
坐标系的选取很重要
对于直线运动,最好沿着这条直线建立坐标系,即建立一个一维直线坐标系。
小球的位移为: x=v0t
小球的位移为: y=gt2/2
以抛出点为坐标原点;初速度v0的方向为x 轴的正方向;竖直向下的方向为y 轴正方向
研究的问题是:
1、速度
2、位移
举例:水平抛出的小球的运动
v0
P(x,y)
O
y
x
s
θ
小球运动的位移
x
y
小球运动的速度
飞机起飞时以300km/h的速度斜向上飞,飞行方向与水平方面的夹角30o。求水平方向的分速度vx和竖直方向的分速度vy
请同学们思考并独立完成
例题1:书本第4页
实验分析
实验装置
实验1
实验2
演示实验:阅读课本P5页演示实验
超连接
实验分析
实验分析:
实验1:红蜡块R沿玻璃管匀速上升,做直线运
动。红蜡块R由A到B,它的位移是AB。
实验2:红蜡块在上升的同时,玻璃管水平向
右匀速移动,红蜡块实际上是斜向右上
方运动的。红蜡块将沿直线AC到达C,
位移是AC。
红蜡块同时参与了两个运动:
1.在玻璃管中竖直向上的运动(由A到B)
2.随玻璃管水平向右的运动(由A到D)
结论:红蜡块实际发生的运动是这两个运动合成的结果
合运动和分运动
分运动:蜡块沿玻璃管在竖直方向的运动和随管做的水平方向的运动,叫做分运动。
合运动:蜡块实际发生的运动叫做合运动
合位移(速度、加速度):合运动的位移 ( 速度、加速度 )
分位移(速度、加速度):分运动的位移( 速度、 加速度)
等时性 各分运动与合运动同时发生和结束,时间相同
等效性 各分运动的共同效果与合运动的效果相同
同体性 各分运动与合运动是同一物体的运动
独立性 各分运动之间互不相干,彼此独立,互不影响
结论: 运动的合成和分解遵循平等四边形定则。
思考1:位移、速度、加速度是标量
还是矢量?
思考2:如何对位移、速度、加速度
进行合成和分解?
思考3:如何对运动进行合成和分解?
练习1:已知蜡块在水平方向的速度为Vx=4cm/s,在竖直方向的速度为Vy=3cm/s,求蜡块运动的速度。
已知分运动求合运动的过程——运动的合成
练习2:书本第7页第2题
练2拓展:跳伞员从高空自由下落,落地前的遇到水平方向吹来的风,则跳伞员在空中下落的时间与无风时比较将( )
A.增长 B.不变 C.缩短 D.无法确定
【解析】选B.根据运动的独立性可知,水滴在竖直方向上的运动和水平方向上的运动互不干涉,其下落时间仅取决于竖直下落的高度,因此选项B正确.
1)是直线运动还是曲线运动?(判断轨迹)
2)是匀变速运动还是变加速运动?(判断运动性质)
思考:如何判断两个直线运动的合运动的运动轨迹和运动性质?
合力F合的方向(或加速度a的方向)与合速度v合的方向是否同一直线
合力(或加速度)是否恒定
练习4.关于互成角度的两个初速度不为零的匀变速直线运动的合运动,下述说法正确的是( )
A.一定是直线运动 B.一定是曲线运动
C. 可能是直线运动,也可能是曲线运动 D.以上都不对
【解析】选C.两个运动的初速度合成、加速度合成如图所示.当a和v重合时,物体做直线运动;当a和v不重合时,物体做曲线运动.由于题目没有给出两个运动的加速度和初速度的具体数值,所以以上两种情况都有可能.选项C正确.
匀加速直线运动
加速曲线运动
画图分析两个加速运动的合成
(一定是匀速直线运动)
2、两互成角度的初速为零的匀加速直线运动的合成
(一定是匀加速直线运动)
3、两互成角度的初速不为零的匀加速直线运动的合成
(匀变速直线运动或匀变速曲线运动)
4、一个匀速直线运动和一个匀加速直线运动的合成
(匀变速直线运动或匀变速曲线运动)
1、两互成角度的匀速直线运动的合成
课堂训练
河宽d=100m,水流速度v1=3m/s,船在静水中的速度是v2=4m/s。求
(1)欲使船渡河时间最短,船应怎样渡河?最短时间是多少?船经过的位移多大?
(2)欲使船渡河距离最短,船应怎样渡河?渡河时间多长?
小船渡河
在流动的河水中渡河的轮船的运动可分解为两个运动:
假设轮船不开动,轮船随水流一起向下游运动;
假设河水不流动,轮船相对河水的运动。
分析1:航程最短
θ
d
分析小船的运动
(1)如果要求船划到对岸航程最短,则船头应指向什么方向?最短航程是多少?所用时间多少?
v水
v合
v船
d
θ
总结:渡河的最短位移大小就是河宽,但是实现这一最短位移,必须满足船在静水的速度大于河水的速度。
分析2:时间最短
d
(2)如果要求船划到对岸时间最短,则船头应指向什么方向?最短时间是多少?航程是多少?
d
θ
A
B
C
总结、渡河的时间最短则船头指向必须和河岸垂直,不受河水速度大小的影响。
v水
v合
v船
上题中,如果水速V水=3m/s,船在静水中的速度V船=4m/s,结果如何呢?
如果河水的速度大于船在静水的速度时,这时船不可能垂直渡河,但仍存在最短位移,求解的方法如下:
d
θ
V合
V水
V船
②渡河的最短位移
v船 < v水的情况
v水
smin
D
O
A
v
小船渡河问题
v船
B
上游
下游
在高处拉低处小船时,通常在河岸上通过滑轮用钢绳拴船,若拉绳的速度为4m/s,当拴船的绳与水平方向成60°时,船的速度是多少?
提示:将船的运动分解成沿绳方向的运动和垂直绳方向的运动。
课堂练习
小结
一、合运动和分运动
1、概念:如果物体同时参与了几个运动,那么物体实际发生的运动就叫做那几个运动的合运动,那几个运动叫做这个实际运动的分运动。
2、合运动和分运动的关系
等效性、独立性、等时性
二、运动的合成和分解
1、遵循平行四边形法则
2、两个直线运动的合成可以是直线运动,也可以是曲线运动。
