人教版中考数学复习专题——借考题实现建模,用模型巧解考题
文档属性
| 名称 | 人教版中考数学复习专题——借考题实现建模,用模型巧解考题 |  | |
| 格式 | zip | ||
| 文件大小 | 216.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-06 11:33:03 | ||
图片预览


文档简介
借考题实现建模 用模型巧解考题
考题是命题老师集体数学智慧的结晶,是数学方法,数学思想,数学智慧的结合体,具有鲜
明的典型性,代表性,探索性,是建模创新,提升数学核心素养的高效载体。
一、试题呈现
(2019年南京)在△ABC中,AB=4,∠C=60°,∠A>∠B,则BC的长的取值范围是 .
二、试题简析
以圆为知识背景,以弦长及其所对圆周角为条件,以特殊角为解题基础,以直径是圆中最长
的弦为依据,确定弦的一个端点取值范围,采用数形结合思想,分类思想,最值思想,建模
思想,为全面提高数学核心素养,搭建一个科学性,探索性,创新性,应用性的平台。
三、解法赏析
作△ABC的外接圆⊙O,如图1所示,作AB的垂直平分线MD,交AB于点,交⊙O于点M,根据圆的对称性,知当点C与点M重合时,AC=BC,∠BAC=∠ABC,因为∠C=60°,所以△ABC是等边三角形,所以BC=AB=4。因为∠BAC>∠ABC,所以BC>AC,所以点C一定位于点M的左侧,所以BC的最小值为4,且取不到;因为BC是⊙O的弦,所以当BC为直径时,最长,连接OA,OB,因为∠C=60°,根据垂径定理,圆心角与圆周角关系定理,得∠AOD=∠BOD=∠ACB=60°,所以∠OAD=30°,所以OA=2OD,AD=2,所以AO=,所以直径BC=2OA=,所以BC长的取值范围是4<BC≤。
四、反思与建模
这是一道多知识综合运用的好题:直径上的圆周角是直角;垂径定理;圆周角与圆心角关系定理;直径最长原理;同一三角形中,大角对大边原理等都是计算解题的关键.仔细观察
条件,可以从中构建出如下几种计算模型:
模型1、构造直径计算模型
设△ABC 是⊙O的内接三角形,∠A的对边是a,∠B的对边是b,∠C的对边是c,⊙O的半径为R。则。
证明:
如图2,作圆的直径CD,连接BD,则∠A=∠D,∠CBD是直角,在直角三角形CBD中,
SinD=,所以sinA=,所以CD=,所以2R=,同理可证:2R=,
2R=,所以。变式:a=2RsinA,b=2RsinB,c=2RsinC。
模型特点:
,大家都会惊叹它外在的形式之美,简 洁 、对称 、和谐 、
统一 ,它 给 人的美感是“悦 目”.[1]涉及量少,只涉及三角形的一边和这边的对角的
正弦值,外接圆的半径,应用时,只要满足上述的三个条件,就可以大胆地用这个模型解题
从而大大提高解题的准确率和解题效率。这个模型贯穿了数学的建模思想[2]。
模型2、构造最值计算模型
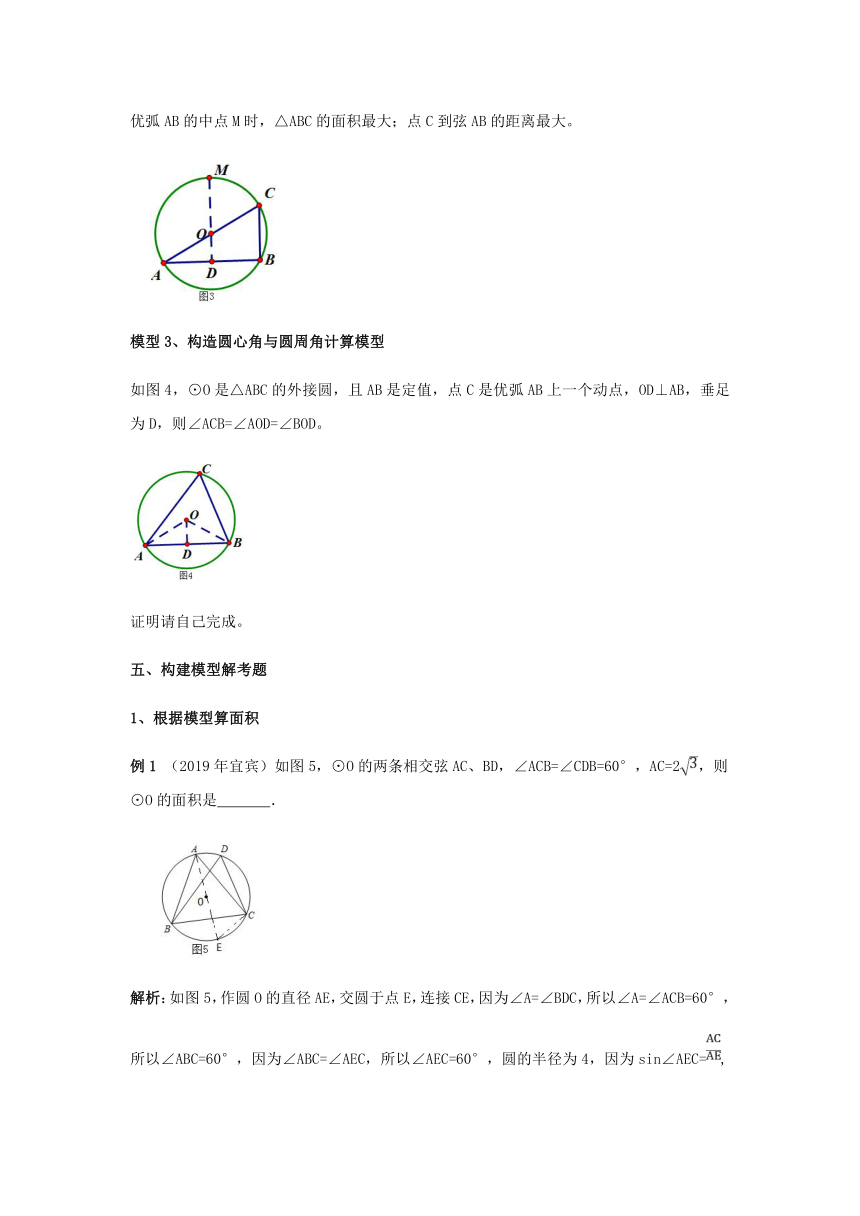
如图3,⊙O是△ABC的外接圆,且AB是定值,点C是优弧AB上一个动点,则当点C位于优弧AB的中点M时,△ABC的面积最大;点C到弦AB的距离最大。
模型3、构造圆心角与圆周角计算模型
如图4,⊙O是△ABC的外接圆,且AB是定值,点C是优弧AB上一个动点,OD⊥AB,垂足为D,则∠ACB=∠AOD=∠BOD。
证明请自己完成。
五、构建模型解考题
1、根据模型算面积
例1 (2019年宜宾)如图5,⊙O的两条相交弦AC、BD,∠ACB=∠CDB=60°,AC=2,则⊙O的面积是 .
解析:如图5,作圆O的直径AE,交圆于点E,连接CE,因为∠A=∠BDC,所以∠A=∠ACB=60°,
所以∠ABC=60°,因为∠ABC=∠AEC,所以∠AEC=60°,圆的半径为4,因为sin∠AEC=,
所以AE==4,所以⊙O的面积是16π,所以应该填16π.
点评:构造适当的直径把已知角,已知都集中到一个直角三角形中是解的关键.
2、根据模型求最值
例2(2019?广元)如图6,△ABC是⊙O的内接三角形,且AB是⊙O的直径,点P为⊙O上
的动点,且∠BPC=60°,⊙O的半径为6,则点P到AC距离的最大值是 .
解析:如图6,过O作OM⊥AC于M,延长MO交⊙O于P,则此时,点P到AC的距离最大,且点P到AC距离的最大值=PM,因为OM⊥AC,∠A=∠BPC=60°,⊙O的半径为6,
所以OP=OA=6,所以OM=OA=×6=3,所以PM=OP+OM=6+3,所以点P到AC距离的最大值是6+3,所以答案为6+3.
点评:圆上动点到定弦距离的最大值就是垂直平分线弦的直径的两个端点到弦的距离,这是垂径定理的应用,也是直径是圆中最大的弦的应用。此法也是用于在拱形中计算最值。
3、根据模型探索角之间的关系式
例3(2019年杭州)如图7,已知锐角三角形ABC内接于⊙O,OD⊥BC于点D,连接OA。
(1)若∠BAC=60°,①求证:OD=OA。②当OA=1时,求△ABC面积的最大值。
(2)点E在线段OA上,OE=OD。连接DE,设∠ABC=m∠OED。∠ACB=n∠OED(m,n是正数)。若∠ABC<∠ACB,求证:m-n+2=0。
解析:(1)①证明:如图7,连接OB,OC,因为OB=OC,OD⊥BC,所以∠B0D=∠COD=∠BAC=60°,
所以∠OBD=30°,所以OD=OB= OA。
②根据模型2,可知当点A,O,D在同一直线上时,三角形ABC的面积最大。因为OA=1,由①知,BC=2BD=,最大高为1+=,所以△ABC的最大面积为:××=。(2)第二问是本题的最大靓点,特点有二,一是提供了一题多解的平台,为提升数学素养提供机遇;二是提供了探索引申、推广的平台,为数学创新思维搭建平台。
解法1:圆心角中心法
因为OE=OD,所以∠OED=∠ODE=x,因为∠ABC=m∠OED=mx,∠ACB=n∠OED=nx,
所以∠AOC=2mx,∠AOB=2nx,∠DOC=180°-mx-nx,因为∠OED+∠ODE+∠EOD=180°,
所以x+x+2mx+180°-mx-nx=180°,整理,得 m-n+2=0。
点评:这种解法有四个特点:把圆周角同一转化为对应的圆心角;巧用圆心角的和为360°,表达未知圆心角的度数;三是用垂径定理确定解题需要角的表达式;最后是在指定三角形中使用三角形内角和定理,这是等式的基础。
解法2:直角三角形两锐角互余法
如图8,延长EO,交BC于点F,连接OB,根据题意,得∠DOF=2x,∠BAF=90°-×2nx=90°-nx,
在直角三角形DOF中,∠DOF+∠OFD=90°,所以2x+ mx+90°-nx=90°,所以m-n+2=0。
点评:延长法构造直角三角形,为直角三角形两锐角互余创造条件,也为问题得解提供新思路,值得熟练掌握。
解法3:构造平行线法
如图9,延长OD交圆于点F,连接AF,BF,CF,因为OE=OD,OA=OF,所以OE:OA=OD:OF,所以DE∥AF,所以∠OED=∠OAF=x,根据垂径定理,得∠BAF=∠CAF=∠BAO+∠OAF,
所以(180°-mx-nx)=x+90°-nx,整理,得m-n+2=0。
点评:利用平行线分线段成比例定理,把等角外移,借助垂径定理,构造角的平分线,利用角的和为基本等量关系构造等式,实现解题目标,奇思异想,彰显数学智慧。
条件∠ABC<∠ACB在这里的意义是什么?去掉这个条件,你能得到怎样的结论?于是,得到如下引申:
如图7,已知锐角三角形ABC内接于⊙O,OD⊥BC于点D,连接OA。
(1)若∠BAC=60°,①求证:OD=OA。②当OA=1时,求△ABC面积的最大值。
(2)点E在线段OA上,OE=OD。连接DE,设∠ABC=m∠OED。∠ACB=n∠OED(m,n是正数)。求证:|m-n|=2。
请自己利用分来的思想完成引申的证明吧!
一道好的考题题,往往是宽入口,有多途径解决方案的问题,并能使不同的人尽可能找到成功的体验,更好地体现考试的信度和效度的问题。[3]通过一多解,一题多构模型的数学问题解决意识的锻炼,固学提能,融会知识,提升数学智慧,培养数学创新精神,实现真正的落实数学核心素养。
[1] 杨丽华 。 欣赏正弦定理之美[J]。中学数学高中版, 2013(5):86。
[2] 侯凯元 。 正弦定理在生活中的应用[J]。智富时代, 2017(4):412。
[3] 苏建强 。 一道耐人寻味的中考压轴题[J]。中学数学杂志, 2019(8):59-61。
同课章节目录
