高中物理人教版能力提升练习 选修3-2第5章 交变电流的产生和描述 Word版含解析
文档属性
| 名称 | 高中物理人教版能力提升练习 选修3-2第5章 交变电流的产生和描述 Word版含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 329.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-05 00:00:00 | ||
图片预览




文档简介
1.(多选)一矩形线圈在匀强磁场中绕垂直磁场方向的轴匀速转动,当线圈通过中性面时,以下说法正确的是 ( )
A.线圈中的感应电动势为零
B.线圈平面与磁感线方向垂直
C.通过线圈的磁通量达到最大值
D.通过线圈的磁通量变化率达到最大值
【解析】选A、B、C。在中性面时,线圈与磁场垂直,磁通量最大。通过线圈的磁通量变化率为零,感应电动势为零,故A、B、C正确,D错误。
2.如图所示,矩形线框置于竖直向下的磁场中,通过导线与灵敏电流表相连,线框在磁场中绕垂直于磁场方向的转轴匀速转动,图中线框平面处于竖直面内。下述说法正确的是 ( )
A.因为线框中产生的是交变电流,所以电流表示数始终为零
B.线框通过图中位置瞬间,穿过线框的磁通量最大
C.线框通过图中位置瞬间,通过电流表的电流瞬时值最小
D.若使线框转动的角速度增大一倍,那么通过电流表电流的有效值也增大一倍
【解析】选D。线框在匀强磁场中匀速转动时,在中性面即线框与磁感线垂直时,磁通量最大,感应电动势最小,而在题中图示位置线框与磁感线平行,磁通量最小,感应电动势最大,故A、B、C错误;电流的有效值I=,现在其余的量都不变,角速度增大一倍后,电流也增大一倍,故D正确。
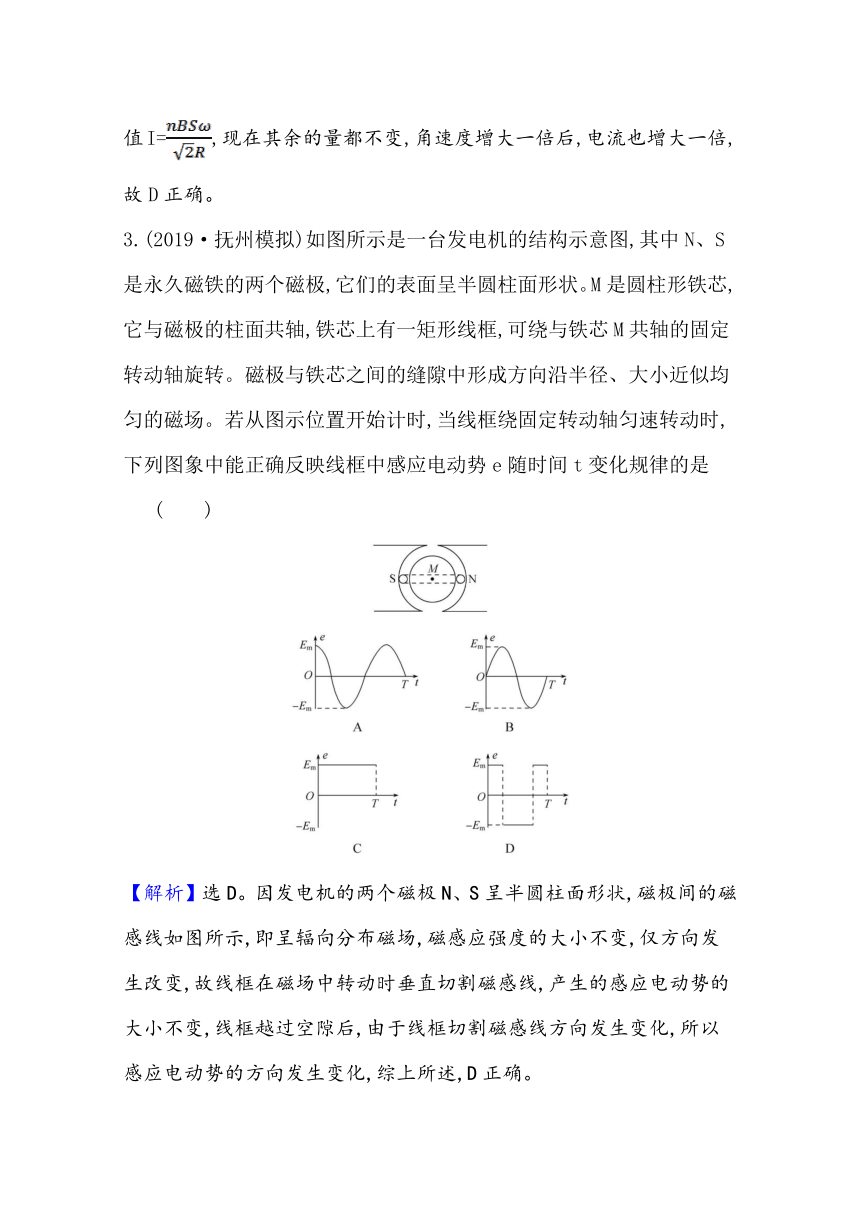
3.(2019·抚州模拟)如图所示是一台发电机的结构示意图,其中N、S是永久磁铁的两个磁极,它们的表面呈半圆柱面形状。M是圆柱形铁芯,它与磁极的柱面共轴,铁芯上有一矩形线框,可绕与铁芯M共轴的固定转动轴旋转。磁极与铁芯之间的缝隙中形成方向沿半径、大小近似均匀的磁场。若从图示位置开始计时,当线框绕固定转动轴匀速转动时,下列图象中能正确反映线框中感应电动势e随时间t变化规律的是 ( )
【解析】选D。因发电机的两个磁极N、S呈半圆柱面形状,磁极间的磁感线如图所示,即呈辐向分布磁场,磁感应强度的大小不变,仅方向发生改变,故线框在磁场中转动时垂直切割磁感线,产生的感应电动势的大小不变,线框越过空隙后,由于线框切割磁感线方向发生变化,所以感应电动势的方向发生变化,综上所述,D正确。
4.单匝矩形线圈在匀强磁场中匀速转动,转动轴垂直于磁场。若线圈所围面积的磁通量随时间变化的规律如图所示,则 ( )
A.线圈中0时刻感应电动势最小
B.线圈中B时刻感应电动势为零
C.线圈中C时刻感应电动势最大
D.线圈从0至C时间内平均感应电动势为0.4 V
【解题指南】(1)Φ-t函数图线的斜率表示,也就是感应电动势E。
(2)计算感应电动势的平均值,应用法拉第电磁感应定律求解。
【解析】选D。由题图知,在t=0时刻磁通量最小,但磁通量的变化率最大,故产生感应电动势最大,故A错误;同理C时刻磁通量的变化率等于零,所以电动势为零,故B、C错误;线圈从0至C时间内平均感应电动势,根据E=n=0.4 V,故D正确。
5.如图所示,在匀强磁场中匀速转动的单匝矩形线圈的周期为T,转轴O1O2垂直于磁场方向,线圈电阻为2 Ω,从线圈平面与磁场方向平行时开始计时,线圈转过60°时的感应电流为1 A,那么 ( )
A.线圈中感应电流的有效值为2 A
B.任意时刻线圈中的感应电动势为e=4cost(V)
C.任意时刻穿过线圈的磁通量为Φ=sint(Wb)
D.从图示位置开始到线圈转过60°时的过程中,线圈中的平均电流为0.5 A
【解题指南】解答本题可按以下思路进行:
(1)根据正弦式交变电流有效值和峰值关系可求电流有效值。
(2)根据Em=Imr可求感应电动势的最大值。
(3)任意时刻穿过线圈的磁通量为Φ=BSsint,根据Em=NBSω可求Φm=BS=。
【解析】选B。从垂直中性面开始其瞬时表达式为i=Imcos θ,则电流的最大值为 Im=;则电流的有效值I== A= A;故A错误; 感应电动势的最大值为 Em=ImR=2×2=4 V,任意时刻线圈中的感应电动势为 e=Emcos t;故B正确;任意时刻穿过线圈的磁通量为Φ=BSsin ,根据公式Em=BSω=Φm可得:Φm=
,故Φ=sint;故C错误;线圈转过60°时的磁通量:Φ=·sin 60°=,从图示位置开始到线圈转过60°时的过程中,线圈中的平均电流为:===
== A。故D错误。
6.正弦交变电压u=50sin314t(V)加在一氖管的两端,已知当氖管两端的电压达到25 V时才开始发光,则此氖管在一个周期内发光的总时间为 ( )
A.0.02 s B.0.002 5 s C.0.01 s D.0.005 s
【解析】选C。根据交流电的瞬时表达式画出U-t图象,如图所示:
当瞬时值为U=25 V时,对应于四个时刻(一个周期内),即:25=50sin314t(V),sin314t=,
所以t1= s、t2= s、t3= s、t4= s,
所以t总=2× s=0.01 s,故选C。
7.先后用不同的交流电源给同一盏灯泡供电,第一次灯泡两端的电压随时间按正弦规律变化(如图甲所示);第二次灯泡两端的电压变化规律如图乙所示。若甲、乙图中的U0、T所表示的电压、周期值是相同的,则以下说法正确的是 ( )
A.第一次,灯泡两端的电压有效值是
B.第二次,灯泡两端的电压有效值是
C.第一、第二次,灯泡的电功率之比是2∶9
D.第一、第二次,灯泡的电功率之比是1∶5
【解析】选D。第一次,灯泡两端电压的有效值为U1=,功率P1==。第二次,设灯泡两端电压的有效值为U2,则·+·=T,解得U2= U0,功率P2==,则P1∶P2=1∶5,故A、B、C错误,D正确。
8.某研究小组成员设计了一个如图所示的电路,已知定值电阻R并联的是一个理想交流电压表,D是理想二极管(正向电阻为零,反向电阻为无穷大)。在A、B间加一交流电压,瞬时值的表达式为u=20sin100xt(V),则交流电压表示数为 ( )
A.10 V B.20 V C.15 V D.14.1 V
【解析】选A。二极管具有单向导电性,使得半个周期内R通路,另半个周期内R断路。设交流电压表示数为U,则一个周期内的电阻发热为Q=T=×T,解得U=10 V。故A正确,B、C、D错误。故选A。
【补偿训练】
如图甲所示是某种型号的电热毯的电路图,电热毯接在交变电源上,通过装置P使加在电热丝上的电压的波形如图乙所示。此时接在电热丝两端的交流电压表的读数为 ( )
A.110 V B.156 V C.220 V D.311 V
【解析】选B。由图象可知该交变电流的周期为T=2×10-2s。可分两段0~0.01 s和0.01~0.02 s,根据有效值的定义可得:×=×T,解得U== V=
156 V,故B正确,A、C、D错误。
9.如图甲所示,在匀强磁场中,两个匝数相同的正方形金属线圈分别以不同的转速绕与磁感线垂直的轴匀速转动,产生的交变电动势e随时间t变化的图象如图乙中曲线 a、b所示,则 ( )
A.t=0时刻,两线圈均处于垂直于中性面的位置
B.a、b对应的线圈转速之比为2∶3
C.a、b对应的两线圈面积之比为1∶1
D.若只改变两线圈的形状(匝数不变),则两线圈电动势的有效值之比一定不变
【解析】选C。t=0时刻,两线圈感应电动势均为零,故两线圈均处于中性面的位置,选项A错误;由图线可知,两线圈的周期之比Ta∶Tb=2∶3;故根据n=可知a、b对应的线圈转速之比为3∶2,选项B错误;根据Em=NBωS可知,==;
==;则==,选项C正确;若只改变两线圈的形状(匝数不变),则两线圈的面积要变化,故感应电动势的最大值要变化,电动势的有效值之比可能变化,选项D错误。
10.如图所示为一个小型旋转电枢式交流发电机的原理图,其矩形线圈的长度ab=0.25 m,宽度bc=0.20 m,共有n=100匝,总电阻r=1.0 Ω,可绕与磁场方向垂直的对称轴OO′转动。线圈处于磁感应强度B=0.40 T的匀强磁场中,与线圈两端相连的金属滑环上接一个“3.0 V 1.8 W”的灯泡,当线圈以角速度ω匀速转动时,小灯泡消耗的功率恰好为1.8 W。(不计转动轴与电刷的摩擦)
(1)推导发电机线圈产生感应电动势的最大值的表达式Em=nBSω(其中S表示线圈的面积)。
(2)求线圈转动的角速度ω。
(3)线圈以上述角速度转动100周过程中发电机产生的电能。
【解析】(1)线圈平面与磁场方向平行时产生的感应电动势最大,设ab边的线速度为v,该边产生的感应电动势为E1=BLabv。
与此同时,线圈的cd边也在切割磁感线,产生的感应电动势为E2=BLcdv。
线圈产生的总感应电动势为Em=n(E1+E2)
因为Lab=Lcd,
所以,Em=n2BLabv。
线速度v=ωLbc,所以Em=nBLabLbcω,而S=LabLbc
(S表示线圈的面积)。
Em=nBSω。
(2)设小灯泡正常发光时的电流为I,则
I==0.60 A,设灯泡正常发光时的电阻为R,
R==5.0 Ω。
根据闭合电路欧姆定律得E=I(R+r)=3.6 V。
发电机感应电动势最大值为Em=E,
Em=nBSω。
解得ω==1.8rad/s≈2.5 rad/s。
(3)发电机产生的电能为Q=IEt,
t=100T=100。
解得Q≈5.43×102 J。
答案:(1)见解析 (2)2.5 rad/s (3)5.43×102 J
11.(多选)如图所示,边长为L的正方形单匝线圈abcd,电阻为r,外电路的电阻为R,ab的中点和cd的中点的连线OO′恰好位于匀强磁场的边界线上,磁场的磁感应强度为B,若线圈从图示位置开始,以角速度ω绕OO′轴匀速转动,则以下判断正确的是 ( )
A.图示位置线圈中的感应电动势最大为Em=BL2ω
B.闭合电路中感应电动势的瞬时值表达式为e=BL2ωsin ωt
C.线圈从图示位置转过180°的过程中,流过电阻R的电荷量为q=
D.线圈转动一周的过程中,电阻R上产生的热量为Q=
【解析】选B、D。题图位置线圈中的感应电动势最小,为零,A错误;若线圈从题图位置开始转动,闭合电路中感应电动势的瞬时值表达式e=BL2ωsin ωt,B正确;线圈从题图位置转过180°的过程中,流过电阻R的电荷量为q=·Δt=
=,C错误;线圈转动一周的过程中,电阻R上产生的热量为Q=()2·
R·=,D正确。
12.如图甲所示,把一个固定的矩形导体线圈水平放置,线圈的两端接一只小灯泡,在线圈所在空间内存在着与线圈平面垂直的磁场。已知线圈的匝数n=100匝,线圈的总电阻r=1.0 Ω,线圈所围成矩形的面积S=0.040 m2,小灯泡的电阻R=
9.0 Ω,磁场的磁感应强度B随时间t的变化规律如图乙所示。已知线圈中产生的感应电动势瞬时值的表达式为e=nBmScost,其中Bm为磁感应强度的最大值,T为磁场变化的周期。不计灯丝电阻随温度的变化,求:
(1)线圈中产生感应电动势的最大值。
(2)小灯泡消耗的电功率。
(3)在磁感应强度变化的0~的时间内,通过小灯泡的电荷量。
【解析】(1)因为线圈中产生的感应电流变化的周期与磁场变化的周期相同,所以由图象可知,线圈中产生交变电流的周期为T=3.14×10-2s。
所以线圈中感应电动势的最大值为
Em=nBmSω=nBmS·=100×1×10-2×0.040×V=8 V。
(2)根据欧姆定律,电路中电流的最大值为
Im==0.80 A
通过小灯泡电流的有效值为I==0.4 A
小灯泡消耗的电功率为P=I2R=2.88 W
(3)在磁感应强度变化的0~周期内,线圈中感应电动势的平均值=nS,通过灯泡的平均电流==,通过灯泡的电荷量Q=Δt==4.0×10-3 C
答案:(1)8 V (2)2.88 W (3)4.0×10-3 C
A.线圈中的感应电动势为零
B.线圈平面与磁感线方向垂直
C.通过线圈的磁通量达到最大值
D.通过线圈的磁通量变化率达到最大值
【解析】选A、B、C。在中性面时,线圈与磁场垂直,磁通量最大。通过线圈的磁通量变化率为零,感应电动势为零,故A、B、C正确,D错误。
2.如图所示,矩形线框置于竖直向下的磁场中,通过导线与灵敏电流表相连,线框在磁场中绕垂直于磁场方向的转轴匀速转动,图中线框平面处于竖直面内。下述说法正确的是 ( )
A.因为线框中产生的是交变电流,所以电流表示数始终为零
B.线框通过图中位置瞬间,穿过线框的磁通量最大
C.线框通过图中位置瞬间,通过电流表的电流瞬时值最小
D.若使线框转动的角速度增大一倍,那么通过电流表电流的有效值也增大一倍
【解析】选D。线框在匀强磁场中匀速转动时,在中性面即线框与磁感线垂直时,磁通量最大,感应电动势最小,而在题中图示位置线框与磁感线平行,磁通量最小,感应电动势最大,故A、B、C错误;电流的有效值I=,现在其余的量都不变,角速度增大一倍后,电流也增大一倍,故D正确。
3.(2019·抚州模拟)如图所示是一台发电机的结构示意图,其中N、S是永久磁铁的两个磁极,它们的表面呈半圆柱面形状。M是圆柱形铁芯,它与磁极的柱面共轴,铁芯上有一矩形线框,可绕与铁芯M共轴的固定转动轴旋转。磁极与铁芯之间的缝隙中形成方向沿半径、大小近似均匀的磁场。若从图示位置开始计时,当线框绕固定转动轴匀速转动时,下列图象中能正确反映线框中感应电动势e随时间t变化规律的是 ( )
【解析】选D。因发电机的两个磁极N、S呈半圆柱面形状,磁极间的磁感线如图所示,即呈辐向分布磁场,磁感应强度的大小不变,仅方向发生改变,故线框在磁场中转动时垂直切割磁感线,产生的感应电动势的大小不变,线框越过空隙后,由于线框切割磁感线方向发生变化,所以感应电动势的方向发生变化,综上所述,D正确。
4.单匝矩形线圈在匀强磁场中匀速转动,转动轴垂直于磁场。若线圈所围面积的磁通量随时间变化的规律如图所示,则 ( )
A.线圈中0时刻感应电动势最小
B.线圈中B时刻感应电动势为零
C.线圈中C时刻感应电动势最大
D.线圈从0至C时间内平均感应电动势为0.4 V
【解题指南】(1)Φ-t函数图线的斜率表示,也就是感应电动势E。
(2)计算感应电动势的平均值,应用法拉第电磁感应定律求解。
【解析】选D。由题图知,在t=0时刻磁通量最小,但磁通量的变化率最大,故产生感应电动势最大,故A错误;同理C时刻磁通量的变化率等于零,所以电动势为零,故B、C错误;线圈从0至C时间内平均感应电动势,根据E=n=0.4 V,故D正确。
5.如图所示,在匀强磁场中匀速转动的单匝矩形线圈的周期为T,转轴O1O2垂直于磁场方向,线圈电阻为2 Ω,从线圈平面与磁场方向平行时开始计时,线圈转过60°时的感应电流为1 A,那么 ( )
A.线圈中感应电流的有效值为2 A
B.任意时刻线圈中的感应电动势为e=4cost(V)
C.任意时刻穿过线圈的磁通量为Φ=sint(Wb)
D.从图示位置开始到线圈转过60°时的过程中,线圈中的平均电流为0.5 A
【解题指南】解答本题可按以下思路进行:
(1)根据正弦式交变电流有效值和峰值关系可求电流有效值。
(2)根据Em=Imr可求感应电动势的最大值。
(3)任意时刻穿过线圈的磁通量为Φ=BSsint,根据Em=NBSω可求Φm=BS=。
【解析】选B。从垂直中性面开始其瞬时表达式为i=Imcos θ,则电流的最大值为 Im=;则电流的有效值I== A= A;故A错误; 感应电动势的最大值为 Em=ImR=2×2=4 V,任意时刻线圈中的感应电动势为 e=Emcos t;故B正确;任意时刻穿过线圈的磁通量为Φ=BSsin ,根据公式Em=BSω=Φm可得:Φm=
,故Φ=sint;故C错误;线圈转过60°时的磁通量:Φ=·sin 60°=,从图示位置开始到线圈转过60°时的过程中,线圈中的平均电流为:===
== A。故D错误。
6.正弦交变电压u=50sin314t(V)加在一氖管的两端,已知当氖管两端的电压达到25 V时才开始发光,则此氖管在一个周期内发光的总时间为 ( )
A.0.02 s B.0.002 5 s C.0.01 s D.0.005 s
【解析】选C。根据交流电的瞬时表达式画出U-t图象,如图所示:
当瞬时值为U=25 V时,对应于四个时刻(一个周期内),即:25=50sin314t(V),sin314t=,
所以t1= s、t2= s、t3= s、t4= s,
所以t总=2× s=0.01 s,故选C。
7.先后用不同的交流电源给同一盏灯泡供电,第一次灯泡两端的电压随时间按正弦规律变化(如图甲所示);第二次灯泡两端的电压变化规律如图乙所示。若甲、乙图中的U0、T所表示的电压、周期值是相同的,则以下说法正确的是 ( )
A.第一次,灯泡两端的电压有效值是
B.第二次,灯泡两端的电压有效值是
C.第一、第二次,灯泡的电功率之比是2∶9
D.第一、第二次,灯泡的电功率之比是1∶5
【解析】选D。第一次,灯泡两端电压的有效值为U1=,功率P1==。第二次,设灯泡两端电压的有效值为U2,则·+·=T,解得U2= U0,功率P2==,则P1∶P2=1∶5,故A、B、C错误,D正确。
8.某研究小组成员设计了一个如图所示的电路,已知定值电阻R并联的是一个理想交流电压表,D是理想二极管(正向电阻为零,反向电阻为无穷大)。在A、B间加一交流电压,瞬时值的表达式为u=20sin100xt(V),则交流电压表示数为 ( )
A.10 V B.20 V C.15 V D.14.1 V
【解析】选A。二极管具有单向导电性,使得半个周期内R通路,另半个周期内R断路。设交流电压表示数为U,则一个周期内的电阻发热为Q=T=×T,解得U=10 V。故A正确,B、C、D错误。故选A。
【补偿训练】
如图甲所示是某种型号的电热毯的电路图,电热毯接在交变电源上,通过装置P使加在电热丝上的电压的波形如图乙所示。此时接在电热丝两端的交流电压表的读数为 ( )
A.110 V B.156 V C.220 V D.311 V
【解析】选B。由图象可知该交变电流的周期为T=2×10-2s。可分两段0~0.01 s和0.01~0.02 s,根据有效值的定义可得:×=×T,解得U== V=
156 V,故B正确,A、C、D错误。
9.如图甲所示,在匀强磁场中,两个匝数相同的正方形金属线圈分别以不同的转速绕与磁感线垂直的轴匀速转动,产生的交变电动势e随时间t变化的图象如图乙中曲线 a、b所示,则 ( )
A.t=0时刻,两线圈均处于垂直于中性面的位置
B.a、b对应的线圈转速之比为2∶3
C.a、b对应的两线圈面积之比为1∶1
D.若只改变两线圈的形状(匝数不变),则两线圈电动势的有效值之比一定不变
【解析】选C。t=0时刻,两线圈感应电动势均为零,故两线圈均处于中性面的位置,选项A错误;由图线可知,两线圈的周期之比Ta∶Tb=2∶3;故根据n=可知a、b对应的线圈转速之比为3∶2,选项B错误;根据Em=NBωS可知,==;
==;则==,选项C正确;若只改变两线圈的形状(匝数不变),则两线圈的面积要变化,故感应电动势的最大值要变化,电动势的有效值之比可能变化,选项D错误。
10.如图所示为一个小型旋转电枢式交流发电机的原理图,其矩形线圈的长度ab=0.25 m,宽度bc=0.20 m,共有n=100匝,总电阻r=1.0 Ω,可绕与磁场方向垂直的对称轴OO′转动。线圈处于磁感应强度B=0.40 T的匀强磁场中,与线圈两端相连的金属滑环上接一个“3.0 V 1.8 W”的灯泡,当线圈以角速度ω匀速转动时,小灯泡消耗的功率恰好为1.8 W。(不计转动轴与电刷的摩擦)
(1)推导发电机线圈产生感应电动势的最大值的表达式Em=nBSω(其中S表示线圈的面积)。
(2)求线圈转动的角速度ω。
(3)线圈以上述角速度转动100周过程中发电机产生的电能。
【解析】(1)线圈平面与磁场方向平行时产生的感应电动势最大,设ab边的线速度为v,该边产生的感应电动势为E1=BLabv。
与此同时,线圈的cd边也在切割磁感线,产生的感应电动势为E2=BLcdv。
线圈产生的总感应电动势为Em=n(E1+E2)
因为Lab=Lcd,
所以,Em=n2BLabv。
线速度v=ωLbc,所以Em=nBLabLbcω,而S=LabLbc
(S表示线圈的面积)。
Em=nBSω。
(2)设小灯泡正常发光时的电流为I,则
I==0.60 A,设灯泡正常发光时的电阻为R,
R==5.0 Ω。
根据闭合电路欧姆定律得E=I(R+r)=3.6 V。
发电机感应电动势最大值为Em=E,
Em=nBSω。
解得ω==1.8rad/s≈2.5 rad/s。
(3)发电机产生的电能为Q=IEt,
t=100T=100。
解得Q≈5.43×102 J。
答案:(1)见解析 (2)2.5 rad/s (3)5.43×102 J
11.(多选)如图所示,边长为L的正方形单匝线圈abcd,电阻为r,外电路的电阻为R,ab的中点和cd的中点的连线OO′恰好位于匀强磁场的边界线上,磁场的磁感应强度为B,若线圈从图示位置开始,以角速度ω绕OO′轴匀速转动,则以下判断正确的是 ( )
A.图示位置线圈中的感应电动势最大为Em=BL2ω
B.闭合电路中感应电动势的瞬时值表达式为e=BL2ωsin ωt
C.线圈从图示位置转过180°的过程中,流过电阻R的电荷量为q=
D.线圈转动一周的过程中,电阻R上产生的热量为Q=
【解析】选B、D。题图位置线圈中的感应电动势最小,为零,A错误;若线圈从题图位置开始转动,闭合电路中感应电动势的瞬时值表达式e=BL2ωsin ωt,B正确;线圈从题图位置转过180°的过程中,流过电阻R的电荷量为q=·Δt=
=,C错误;线圈转动一周的过程中,电阻R上产生的热量为Q=()2·
R·=,D正确。
12.如图甲所示,把一个固定的矩形导体线圈水平放置,线圈的两端接一只小灯泡,在线圈所在空间内存在着与线圈平面垂直的磁场。已知线圈的匝数n=100匝,线圈的总电阻r=1.0 Ω,线圈所围成矩形的面积S=0.040 m2,小灯泡的电阻R=
9.0 Ω,磁场的磁感应强度B随时间t的变化规律如图乙所示。已知线圈中产生的感应电动势瞬时值的表达式为e=nBmScost,其中Bm为磁感应强度的最大值,T为磁场变化的周期。不计灯丝电阻随温度的变化,求:
(1)线圈中产生感应电动势的最大值。
(2)小灯泡消耗的电功率。
(3)在磁感应强度变化的0~的时间内,通过小灯泡的电荷量。
【解析】(1)因为线圈中产生的感应电流变化的周期与磁场变化的周期相同,所以由图象可知,线圈中产生交变电流的周期为T=3.14×10-2s。
所以线圈中感应电动势的最大值为
Em=nBmSω=nBmS·=100×1×10-2×0.040×V=8 V。
(2)根据欧姆定律,电路中电流的最大值为
Im==0.80 A
通过小灯泡电流的有效值为I==0.4 A
小灯泡消耗的电功率为P=I2R=2.88 W
(3)在磁感应强度变化的0~周期内,线圈中感应电动势的平均值=nS,通过灯泡的平均电流==,通过灯泡的电荷量Q=Δt==4.0×10-3 C
答案:(1)8 V (2)2.88 W (3)4.0×10-3 C
