北师大版高中数学必修4第一章《正弦函数的图像》课件(共15张PPT)
文档属性
| 名称 | 北师大版高中数学必修4第一章《正弦函数的图像》课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 325.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-08 11:39:12 | ||
图片预览



文档简介
(共15张PPT)
§5.1 正弦函数的图像
江西省2020年寒假及春季学期延期开学期间线上教育课程
北师大版 高中数学 必修4
第一章 三角函数
一、情景引入
生活中有很多周而复始的变化规律,像抖动绳子、潮汐、声波的振动、简谐运动等都展现了这样的变化规律,那我们如何用数学刻画呢?本章我们所学习的三角函数就是刻画这个规律的模型.
1.
二、温故知新
y
x
O
-1
M
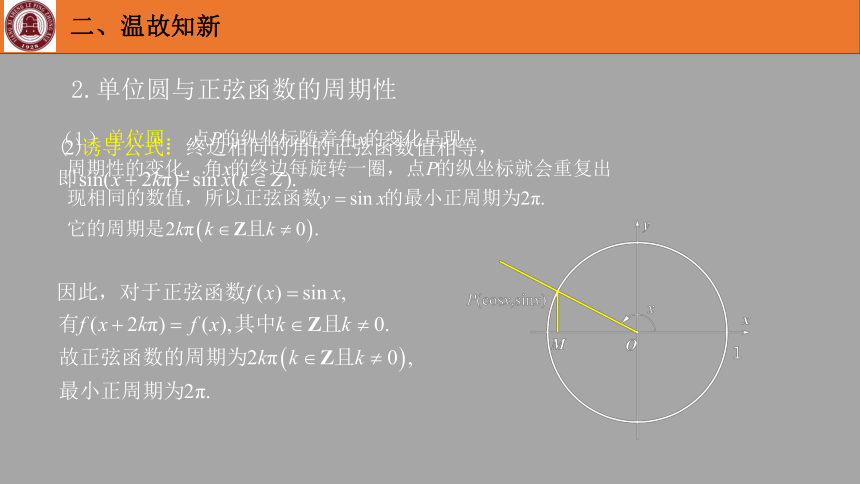
2.单位圆与正弦函数的周期性
二、温故知新
三、新知探究
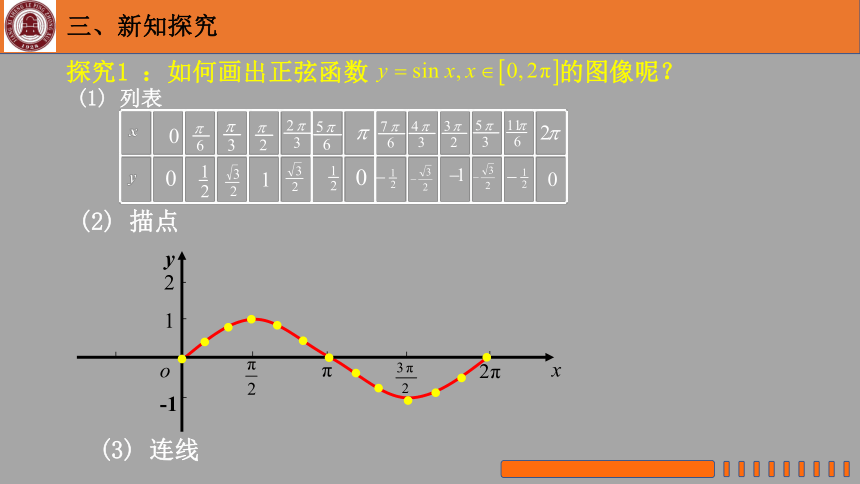
探究1 :如何画出正弦函数 的图像呢?
o
1
y
x
-1
2
(1) 列表
(2) 描点
(3) 连线
三、新知探究
如何在直角坐标系内作出点
O
y
.
.
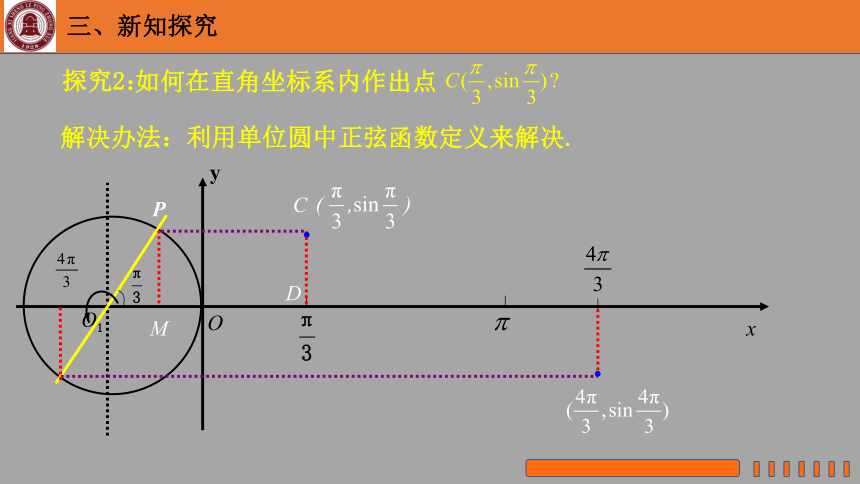
探究2:
解决办法:利用单位圆中正弦函数定义来解决.
x
C
P
M
D
三、新知探究
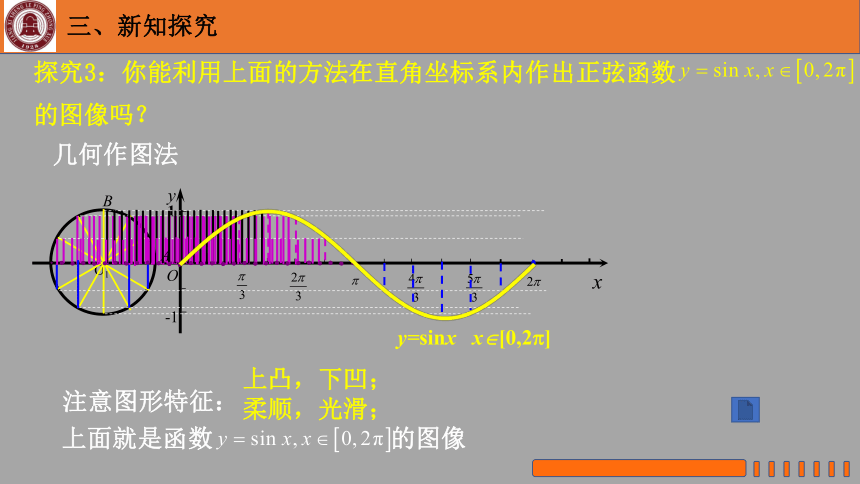
探究3:你能利用上面的方法在直角坐标系内作出正弦函数 的图像吗?
O1
O
y
x
-1
1
A
B
y=sinx x?[0,2?]
几何作图法
上面就是函数 的图像
注意图形特征:
上凸,下凹;
柔顺,光滑;
三、新知探究
探究4:如何画出正弦函数 R的图像?
o
x
y
1
-1
函数y=sinx, x?R的图象
正弦曲线
三、新知探究
探究5:如何画出正弦函数 的简图?
与x轴的交点
图像的最高点
图像的最低点
简图作法
(3)连线(用光滑的曲线顺次连接五个点).
(2)描点(定出五个关键点).
(1)列表(列出对图像形状起关键作用的五点坐标).
x
-1
O
2π
π
1
y
点不在多,五个就行
三、新知探究
思考 “五点法”作图有何优、缺点?
提示: “五点法”就是列表描点法中的一种.它的优点是抓住关键点、迅速画出图像的主要特征;缺点是图像的精度不高.
四、例题讲解
例1用五点法画出函数y= -sinx,x?[0, 2?] 的简图.
o
1
y
x
-1
2
x
y=sinx
y=-sinx
0
0
1
0
-1
0
0
-1
0
1
0
y= -sinx,x?[0, 2?]
y= sinx,x?[0, 2?]
解:
四、例题讲解
例2用五点法画出函数y=sinx+1,x?[0, 2?]的简图.
x
sinx
sinx+1
0 ? 2?
0
1
0
-1
0
1 2 1 0 1
y=sinx,x?[0, 2?]
y=sinx+1,x?[0, 2?]
步骤:
1.列表
2.描点
3.连线
y
x
-1
2
1
o
向上平移1个单位
解:由题意列表如下
五、课堂训练
练习:用“五点法”画出下列函数在区间[0,2π]的简图.
(1)y=sin x - 1; (2)y=3sin x; (3) y=2- sin x .
y=sin x - 1 x∈[0,2π]
y=3sin x x∈[0,2π]
y=2 - sin x x∈[0,2π]
y
0
π
2π
1
-1
x
2
3
六、课堂小结
1.正弦函数的图象
作图
描点法
五点法
几何法
识图
2.注意与三角函数定义,周期等知识的联系
3.正弦函数的图像每相隔2π个单位重复出现,因此只要记住它们在[0,2π]内的图像形状,就可以画出正弦曲线.
4.数学思想方法:数形结合思想,转化与化归思想
六、作业布置
同学们再见!
1.总结本节课的知识,并进一步思考你的学习过程;
2.习题1-5 A组 2题;
3.利用所学知识探究五点法画余弦型函数图像.
§5.1 正弦函数的图像
江西省2020年寒假及春季学期延期开学期间线上教育课程
北师大版 高中数学 必修4
第一章 三角函数
一、情景引入
生活中有很多周而复始的变化规律,像抖动绳子、潮汐、声波的振动、简谐运动等都展现了这样的变化规律,那我们如何用数学刻画呢?本章我们所学习的三角函数就是刻画这个规律的模型.
1.
二、温故知新
y
x
O
-1
M
2.单位圆与正弦函数的周期性
二、温故知新
三、新知探究
探究1 :如何画出正弦函数 的图像呢?
o
1
y
x
-1
2
(1) 列表
(2) 描点
(3) 连线
三、新知探究
如何在直角坐标系内作出点
O
y
.
.
探究2:
解决办法:利用单位圆中正弦函数定义来解决.
x
C
P
M
D
三、新知探究
探究3:你能利用上面的方法在直角坐标系内作出正弦函数 的图像吗?
O1
O
y
x
-1
1
A
B
y=sinx x?[0,2?]
几何作图法
上面就是函数 的图像
注意图形特征:
上凸,下凹;
柔顺,光滑;
三、新知探究
探究4:如何画出正弦函数 R的图像?
o
x
y
1
-1
函数y=sinx, x?R的图象
正弦曲线
三、新知探究
探究5:如何画出正弦函数 的简图?
与x轴的交点
图像的最高点
图像的最低点
简图作法
(3)连线(用光滑的曲线顺次连接五个点).
(2)描点(定出五个关键点).
(1)列表(列出对图像形状起关键作用的五点坐标).
x
-1
O
2π
π
1
y
点不在多,五个就行
三、新知探究
思考 “五点法”作图有何优、缺点?
提示: “五点法”就是列表描点法中的一种.它的优点是抓住关键点、迅速画出图像的主要特征;缺点是图像的精度不高.
四、例题讲解
例1用五点法画出函数y= -sinx,x?[0, 2?] 的简图.
o
1
y
x
-1
2
x
y=sinx
y=-sinx
0
0
1
0
-1
0
0
-1
0
1
0
y= -sinx,x?[0, 2?]
y= sinx,x?[0, 2?]
解:
四、例题讲解
例2用五点法画出函数y=sinx+1,x?[0, 2?]的简图.
x
sinx
sinx+1
0 ? 2?
0
1
0
-1
0
1 2 1 0 1
y=sinx,x?[0, 2?]
y=sinx+1,x?[0, 2?]
步骤:
1.列表
2.描点
3.连线
y
x
-1
2
1
o
向上平移1个单位
解:由题意列表如下
五、课堂训练
练习:用“五点法”画出下列函数在区间[0,2π]的简图.
(1)y=sin x - 1; (2)y=3sin x; (3) y=2- sin x .
y=sin x - 1 x∈[0,2π]
y=3sin x x∈[0,2π]
y=2 - sin x x∈[0,2π]
y
0
π
2π
1
-1
x
2
3
六、课堂小结
1.正弦函数的图象
作图
描点法
五点法
几何法
识图
2.注意与三角函数定义,周期等知识的联系
3.正弦函数的图像每相隔2π个单位重复出现,因此只要记住它们在[0,2π]内的图像形状,就可以画出正弦曲线.
4.数学思想方法:数形结合思想,转化与化归思想
六、作业布置
同学们再见!
1.总结本节课的知识,并进一步思考你的学习过程;
2.习题1-5 A组 2题;
3.利用所学知识探究五点法画余弦型函数图像.
