北师大版高中数学选修2-1第四章《数系的扩充与复数的引入》复习小结课件(共24张PPT)
文档属性
| 名称 | 北师大版高中数学选修2-1第四章《数系的扩充与复数的引入》复习小结课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-08 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
复习小结
在
线
堂
课
北师大版-高中数学选修1-2 第四章 数系的扩充与复数的引入
赣
知识
要点梳理
思想
方法梳理
神秘
的复数
【主要内容】
01
02
03
练习
巩固加深
04
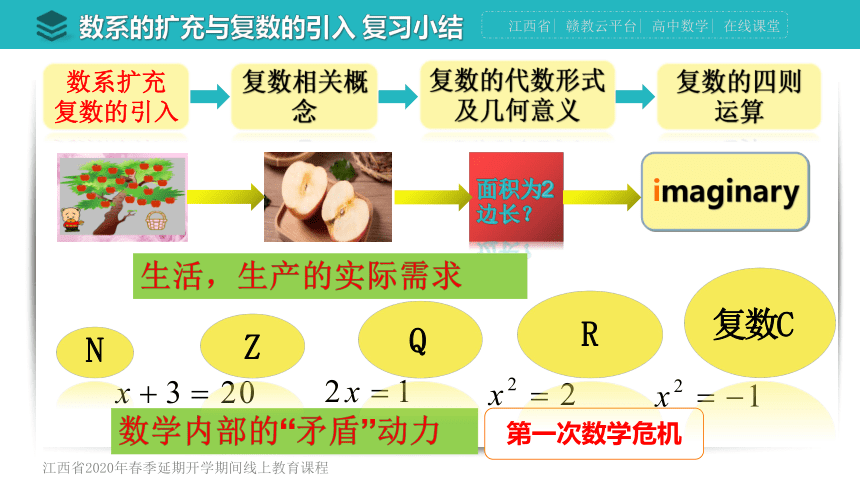
数系扩充
复数的引入
复数相关概念
复数的代数形式及几何意义
复数的四则运算
imaginary
第一次数学危机
面积为2
边长?
生活,生产的实际需求
数学内部的“矛盾”动力
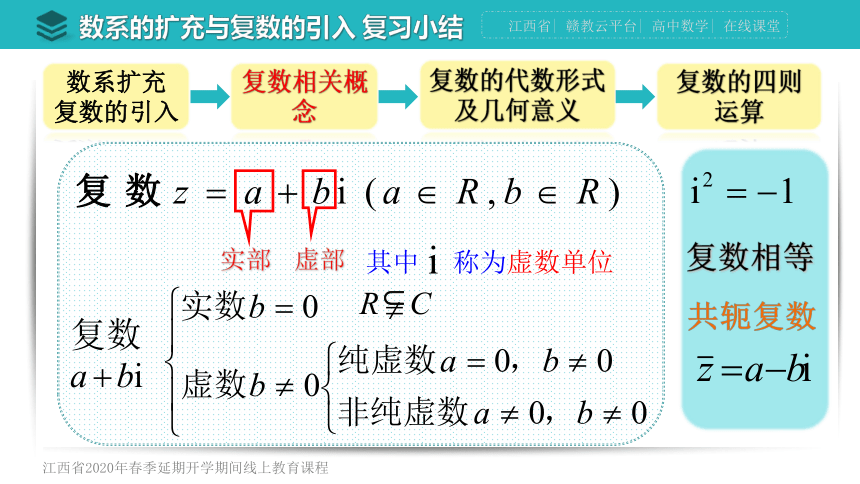
实部
虚部
其中 称为虚数单位
复数
复数相等
共轭复数
数系扩充
复数的引入
复数相关概念
复数的代数形式及几何意义
复数的四则运算
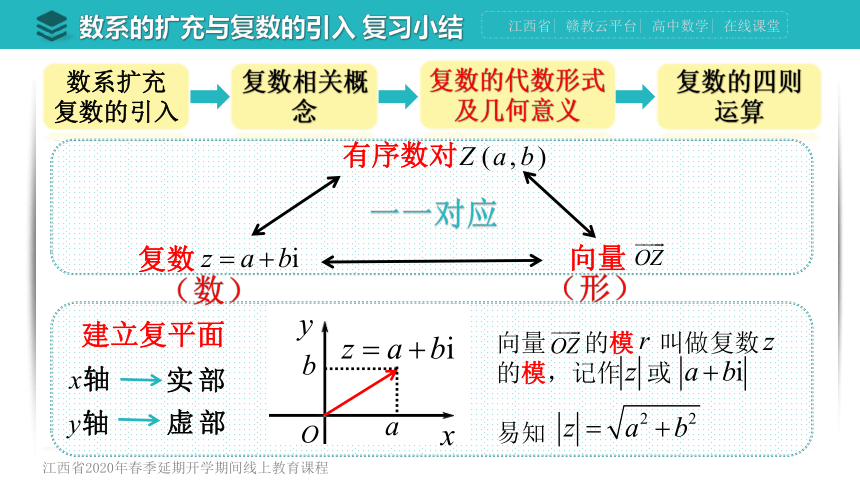
一一对应
(数)
(形)
建立复平面
O
a
b
有序数对
复数
向量
向量 的模 叫做复数 的模,记作 或
易知
数系扩充
复数的引入
复数相关概念
复数的代数形式及几何意义
复数的四则运算
1复数的加减法法则
复数的四则运算
2复数的乘法法则
3复数的除法法则
(与合并同类项类似)
(与多项式相乘类似)
(与分母有理化类似)
数系扩充
复数的引入
复数相关概念
复数的代数形式及几何意义
复数的四则运算
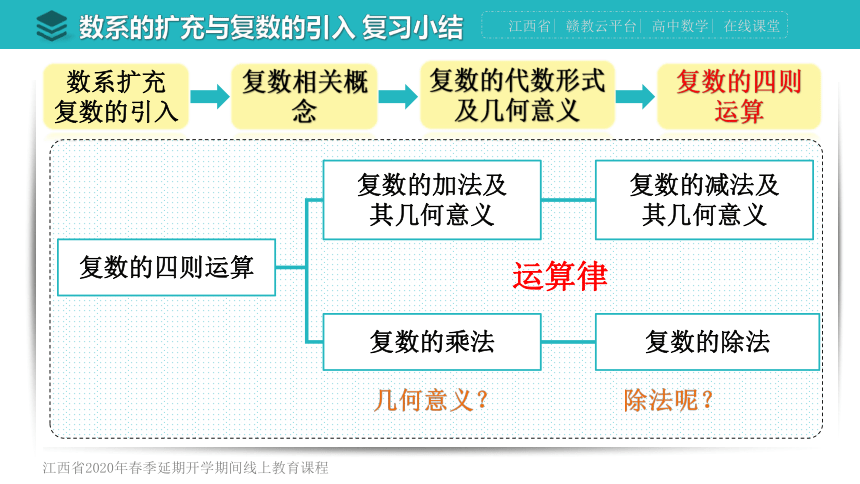
运算律
几何意义?
除法呢?
复数的四则运算
复数的加法及
其几何意义
复数的减法及
其几何意义
复数的乘法
复数的除法
数系扩充
复数的引入
复数相关概念
复数的代数形式及几何意义
复数的四则运算
类比推理
运算一致
多项式及其运算
复数及其运算
平面向量
及其运算
数轴上的向量
及其运算
实数及其运算
有理数及其运算
特殊化
类比
类比
类比
特殊化
数系扩充
复数的引入
复数相关概念
复数的代数形式及几何意义
复数的四则运算
1 思想方法 类比推理,数形结合
2 关键能力 运算求解,直观想象
思想方法梳理
例题讲解
(2)计算 .
(1)计算 并指出其位于复平面的哪个象限;
例1
本题小结:复数四则运算及乘方运算类比多项式运算
解
位于第二象限.
例2
解
待定系数法
因为 ,所以 .
化简得
方程角度
本题小结:方法1 复数代数形式,借助待定系数法求解;
方法2直接当成未知数,解方程
解
例2
例3 已知复数 ,求在复平面内满足 的点的轨迹.
解
几何意义
解
本题小结:分别从复数的代数和几何角度解决相关问题
代数
例3 已知复数 ,求在复平面内满足 的点的轨迹.
神秘
的复数
在复数范围下解方程
代数基本定理
任何复数系一元 次多项式 方程在复数域上至少有一根 ,由此推出, 次复系数多项式方程在复数域内有且只有 个根(重根按重数计算).代数基本定理在代数乃至整个数学中起着基础作用.
神秘
的复数
应用广泛 系统分析 信号分析 量子力学
相对论 反常积分 应用数学 流体力学
万物皆数
——————毕达哥拉斯
思想有多远,“数”就可以到多远
神秘
的复数
神秘
的复数
【课堂小结】
1.以知识链的形式回顾了整章知识
2. 思想方法 类比推理,数形结合
关键能力 运算求解,直观想象
数系扩充
复数的引入
复数相关概念
复数的代数形式及几何意义
复数的四则运算
数系扩充
复数的引入
复数相关概念
复数的代数形式及几何意义
复数的四则运算
3. 随着历史的发展,人们对数的认识也在发生变化,
通过本章的学习,大家对数产生及认识是否多了一些思考?
课后作业
【答案】
谢谢
THANKS
复习小结
在
线
堂
课
北师大版-高中数学选修1-2 第四章 数系的扩充与复数的引入
赣
知识
要点梳理
思想
方法梳理
神秘
的复数
【主要内容】
01
02
03
练习
巩固加深
04
数系扩充
复数的引入
复数相关概念
复数的代数形式及几何意义
复数的四则运算
imaginary
第一次数学危机
面积为2
边长?
生活,生产的实际需求
数学内部的“矛盾”动力
实部
虚部
其中 称为虚数单位
复数
复数相等
共轭复数
数系扩充
复数的引入
复数相关概念
复数的代数形式及几何意义
复数的四则运算
一一对应
(数)
(形)
建立复平面
O
a
b
有序数对
复数
向量
向量 的模 叫做复数 的模,记作 或
易知
数系扩充
复数的引入
复数相关概念
复数的代数形式及几何意义
复数的四则运算
1复数的加减法法则
复数的四则运算
2复数的乘法法则
3复数的除法法则
(与合并同类项类似)
(与多项式相乘类似)
(与分母有理化类似)
数系扩充
复数的引入
复数相关概念
复数的代数形式及几何意义
复数的四则运算
运算律
几何意义?
除法呢?
复数的四则运算
复数的加法及
其几何意义
复数的减法及
其几何意义
复数的乘法
复数的除法
数系扩充
复数的引入
复数相关概念
复数的代数形式及几何意义
复数的四则运算
类比推理
运算一致
多项式及其运算
复数及其运算
平面向量
及其运算
数轴上的向量
及其运算
实数及其运算
有理数及其运算
特殊化
类比
类比
类比
特殊化
数系扩充
复数的引入
复数相关概念
复数的代数形式及几何意义
复数的四则运算
1 思想方法 类比推理,数形结合
2 关键能力 运算求解,直观想象
思想方法梳理
例题讲解
(2)计算 .
(1)计算 并指出其位于复平面的哪个象限;
例1
本题小结:复数四则运算及乘方运算类比多项式运算
解
位于第二象限.
例2
解
待定系数法
因为 ,所以 .
化简得
方程角度
本题小结:方法1 复数代数形式,借助待定系数法求解;
方法2直接当成未知数,解方程
解
例2
例3 已知复数 ,求在复平面内满足 的点的轨迹.
解
几何意义
解
本题小结:分别从复数的代数和几何角度解决相关问题
代数
例3 已知复数 ,求在复平面内满足 的点的轨迹.
神秘
的复数
在复数范围下解方程
代数基本定理
任何复数系一元 次多项式 方程在复数域上至少有一根 ,由此推出, 次复系数多项式方程在复数域内有且只有 个根(重根按重数计算).代数基本定理在代数乃至整个数学中起着基础作用.
神秘
的复数
应用广泛 系统分析 信号分析 量子力学
相对论 反常积分 应用数学 流体力学
万物皆数
——————毕达哥拉斯
思想有多远,“数”就可以到多远
神秘
的复数
神秘
的复数
【课堂小结】
1.以知识链的形式回顾了整章知识
2. 思想方法 类比推理,数形结合
关键能力 运算求解,直观想象
数系扩充
复数的引入
复数相关概念
复数的代数形式及几何意义
复数的四则运算
数系扩充
复数的引入
复数相关概念
复数的代数形式及几何意义
复数的四则运算
3. 随着历史的发展,人们对数的认识也在发生变化,
通过本章的学习,大家对数产生及认识是否多了一些思考?
课后作业
【答案】
谢谢
THANKS
同课章节目录
