北师大版高中数学选修2-1第四章第1节《数系的扩充与复数的有关概念》课件(共20张PPT)
文档属性
| 名称 | 北师大版高中数学选修2-1第四章第1节《数系的扩充与复数的有关概念》课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-08 11:44:46 | ||
图片预览








文档简介
(共20张PPT)
1 数系的扩充与复数的有关概念
在
线
堂
课
北师大版-高中数学选修1-2第四章:数系的扩充与复数的引入
赣
问题1:同学们能列举一些我们学过的数集,并用字母来表示吗?
问题2:这些数集之间的关系是怎样的?
N Z Q R
N
Z
Q
R
数系的发展历程
思考:为什么要不断扩充数系?
① 分数解决了在整数集中不能整除的矛盾;
② 负数解决了在正有理数集中不够减的矛盾;
③ 无理数解决了开方开不尽的矛盾;
数集的每一次扩充都为了满足社会生产实践的需要.
当数集扩充到实数集R以后,像这样的方程还是无解的,
因为没有一个实数的平方等于,如何解决这个问题?
另一方面,数集的每一次扩充都为了解决数学内部的矛盾.
思考:为什么要不断扩充数系?
数系的扩充
问题:一元二次方程 无实数解.
解决方法:
(1)它的平方等于,即;
引入一个新数,记作 把 叫作虚数单位,并规定:
(2) 可以与实数进行四则运算,进行四则运算时,原有的加、乘运算律仍然成立.
z = a + b i (a,b∈R)
复数的代数形式
实部
虚部
复数的有关概念
1.复数的有关概念
(1)定义:形如a+bi(a,b∈R)的数叫作复数,其中i是虚数单位.
(2)表示方法:复数通常用字母z表示,即
全体复数所成的集合叫作复数集,用C表示
复数的分类
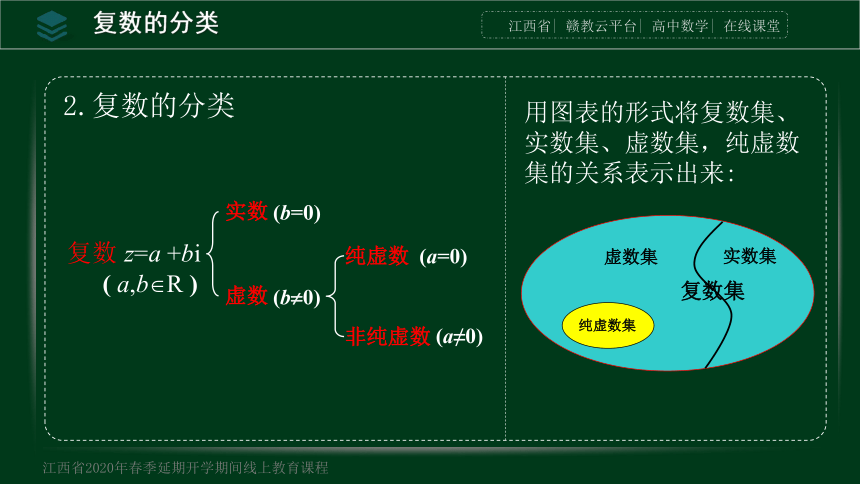
2.复数的分类
实数
虚数
纯虚数
(b=0)
(b?0)
(a=0)
( a,b?R )
复数 z=a +bi
用图表的形式将复数集、实数集、虚数集,纯虚数集的关系表示出来:
(a≠0)
非纯虚数
复数集
虚数集
纯虚数集
实数集
例1 说出下列四个复数的实部、虚部,
并指出它们是实数还是虚数,
如果是虚数请指出是否为纯虚数.
(1); (2); (3); (4)0.
纯虚数:
a=0 且 b≠0
复数的分类
解:
实部
虚部
类型
3
4
虚数
z = a + b i (a,b∈R)
实部
虚部
(1)
(2)
=
0
纯虚数
=
(3)
(4)0
-7
1
虚数
0
0
实数
= () +1
= 0 + 0
提示:对于一元二项式,若对任意都成立,则=___, =___.
两个复数相等的充要条件是实部,虚部分别相等.
特别地,若a,b ∈R, a+bi=0 ? .
a=b=0
复数的相等的条件
思考:对于复数 a+bi 和 c+di (a,b,c,d∈R),你认为满足什么条件时,这两个复数相等?
a+bi = c+di
(a,b,c,d∈R)
?
a=c 且 b=d
例2 设
,
求的值.
解:根据复数相等的定义,得
方程思想
解这个方程组,得
复数的相等的条件
a+bi = c+di
(a,b,c,d∈R)
?
a=c 且 b=d
数轴上的点
类比实数的几何意义,你能否找到用来表示复数的几何模型?
实数可以用数轴上的点来表示.
一一对应
实数
(形)
(数)
复数z=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
(数)
(形)
一一对应
复数的几何意义
x
y
o
z=a+bi
Z(a,b)
b
a
复数的几何意义
x
y
o
z=a+bi
Z(a,b)
b
a
建立平面直角坐标系来表示复数的平面,叫作复数平面(简称复平面).
x轴------实轴
y轴------虚轴
1.复平面的概念
复平面内的点
Z(a,b)
平面向量 (a,b)
一一对应
一一对应
复数 z=a+bi
一一对应
2.复数的模
复数z=a+bi在复平面内的对应的点是Z(a,b) ,我们将点Z(a,b)到原点的距离|OZ|叫做复数的模或绝对值,记作|z|,显然
复数的几何意义
x
y
o
z=a+bi
Z(a,b)
b
a
复平面内的点
Z(a,b)
平面向量 (a,b)
一一对应
一一对应
复数 z=a+bi
一一对应
例3 在复平面内表示下列复数,
并分别求出它们的模.
(1); (2);
(3)
解 在复平面内的表示如右图所示,
复数的几何意义
练习 说出图中复平面内点 A,B,C,D,E
所表示的复数.
复数的几何意义
,并计算出这些复数的模.
课堂小结
提出问题
解决问题
复数的概念
分类
相等的条件
几何意义
方程思想
数形结合思想
类比思想
转化思想
课后作业
1.求实数的值,使复数分别是:
(1)实数; (2)纯虚数; (3)零.
2.求适合下列各方程的实数x, y:
(1) ;
(2).
3.在复平面上作出表示下列复数的点:
(1) (2) ; (3); (4)
课后作业
课后作业
1.(1) (2) (3)
2.(1);
(2).
3.如右图所示,对应的点分别为A,B,C,D:
课后作业参考答案
A
B
C
D
祝同学们学习进步!
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
5
4
3
2
1
-1
-2
-3
-4
-5
x
y
A
B
C
D
E
备用坐标系
1 数系的扩充与复数的有关概念
在
线
堂
课
北师大版-高中数学选修1-2第四章:数系的扩充与复数的引入
赣
问题1:同学们能列举一些我们学过的数集,并用字母来表示吗?
问题2:这些数集之间的关系是怎样的?
N Z Q R
N
Z
Q
R
数系的发展历程
思考:为什么要不断扩充数系?
① 分数解决了在整数集中不能整除的矛盾;
② 负数解决了在正有理数集中不够减的矛盾;
③ 无理数解决了开方开不尽的矛盾;
数集的每一次扩充都为了满足社会生产实践的需要.
当数集扩充到实数集R以后,像这样的方程还是无解的,
因为没有一个实数的平方等于,如何解决这个问题?
另一方面,数集的每一次扩充都为了解决数学内部的矛盾.
思考:为什么要不断扩充数系?
数系的扩充
问题:一元二次方程 无实数解.
解决方法:
(1)它的平方等于,即;
引入一个新数,记作 把 叫作虚数单位,并规定:
(2) 可以与实数进行四则运算,进行四则运算时,原有的加、乘运算律仍然成立.
z = a + b i (a,b∈R)
复数的代数形式
实部
虚部
复数的有关概念
1.复数的有关概念
(1)定义:形如a+bi(a,b∈R)的数叫作复数,其中i是虚数单位.
(2)表示方法:复数通常用字母z表示,即
全体复数所成的集合叫作复数集,用C表示
复数的分类
2.复数的分类
实数
虚数
纯虚数
(b=0)
(b?0)
(a=0)
( a,b?R )
复数 z=a +bi
用图表的形式将复数集、实数集、虚数集,纯虚数集的关系表示出来:
(a≠0)
非纯虚数
复数集
虚数集
纯虚数集
实数集
例1 说出下列四个复数的实部、虚部,
并指出它们是实数还是虚数,
如果是虚数请指出是否为纯虚数.
(1); (2); (3); (4)0.
纯虚数:
a=0 且 b≠0
复数的分类
解:
实部
虚部
类型
3
4
虚数
z = a + b i (a,b∈R)
实部
虚部
(1)
(2)
=
0
纯虚数
=
(3)
(4)0
-7
1
虚数
0
0
实数
= () +1
= 0 + 0
提示:对于一元二项式,若对任意都成立,则=___, =___.
两个复数相等的充要条件是实部,虚部分别相等.
特别地,若a,b ∈R, a+bi=0 ? .
a=b=0
复数的相等的条件
思考:对于复数 a+bi 和 c+di (a,b,c,d∈R),你认为满足什么条件时,这两个复数相等?
a+bi = c+di
(a,b,c,d∈R)
?
a=c 且 b=d
例2 设
,
求的值.
解:根据复数相等的定义,得
方程思想
解这个方程组,得
复数的相等的条件
a+bi = c+di
(a,b,c,d∈R)
?
a=c 且 b=d
数轴上的点
类比实数的几何意义,你能否找到用来表示复数的几何模型?
实数可以用数轴上的点来表示.
一一对应
实数
(形)
(数)
复数z=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
(数)
(形)
一一对应
复数的几何意义
x
y
o
z=a+bi
Z(a,b)
b
a
复数的几何意义
x
y
o
z=a+bi
Z(a,b)
b
a
建立平面直角坐标系来表示复数的平面,叫作复数平面(简称复平面).
x轴------实轴
y轴------虚轴
1.复平面的概念
复平面内的点
Z(a,b)
平面向量 (a,b)
一一对应
一一对应
复数 z=a+bi
一一对应
2.复数的模
复数z=a+bi在复平面内的对应的点是Z(a,b) ,我们将点Z(a,b)到原点的距离|OZ|叫做复数的模或绝对值,记作|z|,显然
复数的几何意义
x
y
o
z=a+bi
Z(a,b)
b
a
复平面内的点
Z(a,b)
平面向量 (a,b)
一一对应
一一对应
复数 z=a+bi
一一对应
例3 在复平面内表示下列复数,
并分别求出它们的模.
(1); (2);
(3)
解 在复平面内的表示如右图所示,
复数的几何意义
练习 说出图中复平面内点 A,B,C,D,E
所表示的复数.
复数的几何意义
,并计算出这些复数的模.
课堂小结
提出问题
解决问题
复数的概念
分类
相等的条件
几何意义
方程思想
数形结合思想
类比思想
转化思想
课后作业
1.求实数的值,使复数分别是:
(1)实数; (2)纯虚数; (3)零.
2.求适合下列各方程的实数x, y:
(1) ;
(2).
3.在复平面上作出表示下列复数的点:
(1) (2) ; (3); (4)
课后作业
课后作业
1.(1) (2) (3)
2.(1);
(2).
3.如右图所示,对应的点分别为A,B,C,D:
课后作业参考答案
A
B
C
D
祝同学们学习进步!
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
5
4
3
2
1
-1
-2
-3
-4
-5
x
y
A
B
C
D
E
备用坐标系
同课章节目录
