北师大版高中数学选修2-1第四章第2节《复数的四则运算》课件(共20张PPT)
文档属性
| 名称 | 北师大版高中数学选修2-1第四章第2节《复数的四则运算》课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-08 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第二节 复数的四则运算
北师大版-高中数学选修1-2 第四章 数系的扩充与复数的引入
赣
数还够用吗?
一、数系的扩充
自然数
为了满足基本的计数需要
分数
负数
无理数
为了解决开方开不尽的矛盾
为了解决等额
分配的问题
为了表示具有相反意义的量
为了解决负数开平方的问题
复数
数系的每一次扩充都是由数学实际需求和内部矛盾发展所产生的.
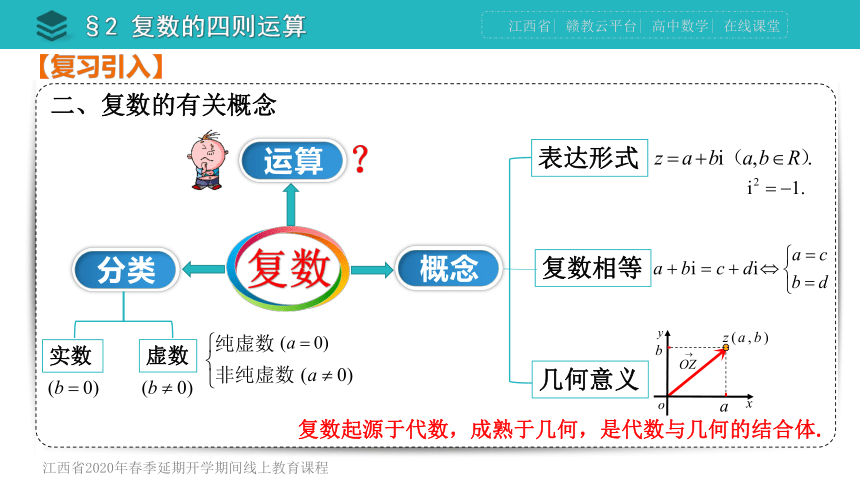
二、复数的有关概念
表达形式
复数相等
实数
虚数
几何意义
复数起源于代数,成熟于几何,是代数与几何的结合体.
1.复数的加减法法则
设a+bi和c+di是任意两个复数,我们定义复数的加法、减法如下:
(a+bi)±(c+di)=
复数的加减法与合并同类项类似.
例1 计算:
两个复数的和(或差)仍然是一个复数,它的实部为原来两个复数的实部与实部的和(或差),它的虚部为原来两个复数的虚部与虚部的和(或差).
(a±c)+(b±d)i.
复数的加法是否满足交换律和结合律呢?
左,右都等于2-i,等式成立.
左,右都等于4-2i,等式成立.
2.复数加法的交换律、结合律
复数是代数与几何的结合体,可以表示为复平面内的向量,那么复数的加减法与向量的加减法是否具有一致性呢?
3.(1)复数加法的几何意义
3.(2)复数减法的几何意义
Z1(a,b)
Z2(c,d)
Z(a-c,b-d)
复数的乘法与多项式的乘法类似,
但要用i2=-1进行化简,并把实部与虚部
分别合并.
1.复数的乘法法则
设a+bi和c+di为任意两个复数,我们定义复数的乘法如下:
(a+bi)(c+di)=(ac-bd)+(ad+bc)i
2.复数乘法的运算律
3.复数的乘方
在复数范围内,实数范围内正整数指数幂的运算律仍然成立,
计算下列各式,你能发现其中有什么规律吗?
4.共轭复数的概念
我们可以发现,每一小题的两个复数,都满足:它们的实部相等,
虚部互为相反数,而且它们的乘积都是一个非负实数.
实部相等
虚部互为相反数
性质:
化虚为实
分析:
i的正整数指数幂的运算规律
发现:
实数的除法是实数的乘法的逆运算,类似地,复数的除法也是复数乘法的逆运算.
1.复数除法的定义
分析:
与分母有理化的方法类似,将两个复数相除的分母实数化;
复数的除法与分母有理化的方法类似.
即:将分母实数化,用分母的共轭复数同乘分子分母,再进行运算.
2.复数的除法法则
一、复数的四则运算
二、数学思想
“类比思想”、“数形结合”以及“从特殊到一般”.
谢谢
THANKS
第二节 复数的四则运算
北师大版-高中数学选修1-2 第四章 数系的扩充与复数的引入
赣
数还够用吗?
一、数系的扩充
自然数
为了满足基本的计数需要
分数
负数
无理数
为了解决开方开不尽的矛盾
为了解决等额
分配的问题
为了表示具有相反意义的量
为了解决负数开平方的问题
复数
数系的每一次扩充都是由数学实际需求和内部矛盾发展所产生的.
二、复数的有关概念
表达形式
复数相等
实数
虚数
几何意义
复数起源于代数,成熟于几何,是代数与几何的结合体.
1.复数的加减法法则
设a+bi和c+di是任意两个复数,我们定义复数的加法、减法如下:
(a+bi)±(c+di)=
复数的加减法与合并同类项类似.
例1 计算:
两个复数的和(或差)仍然是一个复数,它的实部为原来两个复数的实部与实部的和(或差),它的虚部为原来两个复数的虚部与虚部的和(或差).
(a±c)+(b±d)i.
复数的加法是否满足交换律和结合律呢?
左,右都等于2-i,等式成立.
左,右都等于4-2i,等式成立.
2.复数加法的交换律、结合律
复数是代数与几何的结合体,可以表示为复平面内的向量,那么复数的加减法与向量的加减法是否具有一致性呢?
3.(1)复数加法的几何意义
3.(2)复数减法的几何意义
Z1(a,b)
Z2(c,d)
Z(a-c,b-d)
复数的乘法与多项式的乘法类似,
但要用i2=-1进行化简,并把实部与虚部
分别合并.
1.复数的乘法法则
设a+bi和c+di为任意两个复数,我们定义复数的乘法如下:
(a+bi)(c+di)=(ac-bd)+(ad+bc)i
2.复数乘法的运算律
3.复数的乘方
在复数范围内,实数范围内正整数指数幂的运算律仍然成立,
计算下列各式,你能发现其中有什么规律吗?
4.共轭复数的概念
我们可以发现,每一小题的两个复数,都满足:它们的实部相等,
虚部互为相反数,而且它们的乘积都是一个非负实数.
实部相等
虚部互为相反数
性质:
化虚为实
分析:
i的正整数指数幂的运算规律
发现:
实数的除法是实数的乘法的逆运算,类似地,复数的除法也是复数乘法的逆运算.
1.复数除法的定义
分析:
与分母有理化的方法类似,将两个复数相除的分母实数化;
复数的除法与分母有理化的方法类似.
即:将分母实数化,用分母的共轭复数同乘分子分母,再进行运算.
2.复数的除法法则
一、复数的四则运算
二、数学思想
“类比思想”、“数形结合”以及“从特殊到一般”.
谢谢
THANKS
同课章节目录
