高中物理新人教版必修1:4.3《牛顿第二定律》课件(共59张PPT)
文档属性
| 名称 | 高中物理新人教版必修1:4.3《牛顿第二定律》课件(共59张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 940.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-05 16:05:36 | ||
图片预览




文档简介
(共59张PPT)
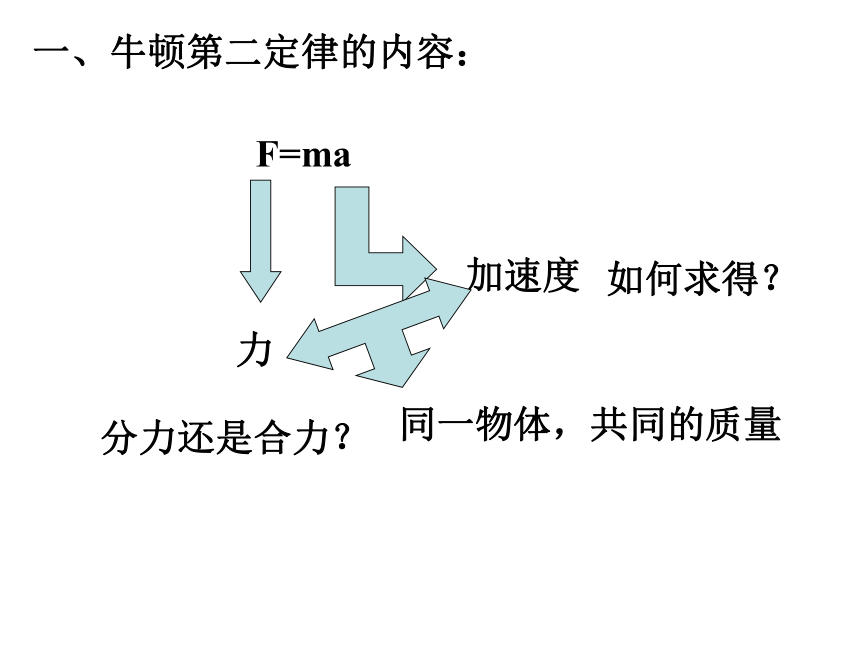
一、牛顿第二定律的内容:
F=ma
力
分力还是合力?
加速度
同一物体,共同的质量
如何求得?
二、必会的几个问题
1、平面上的问题
2、斜面的上的问题
3、竖直方向的问题
二、必会的几个问题
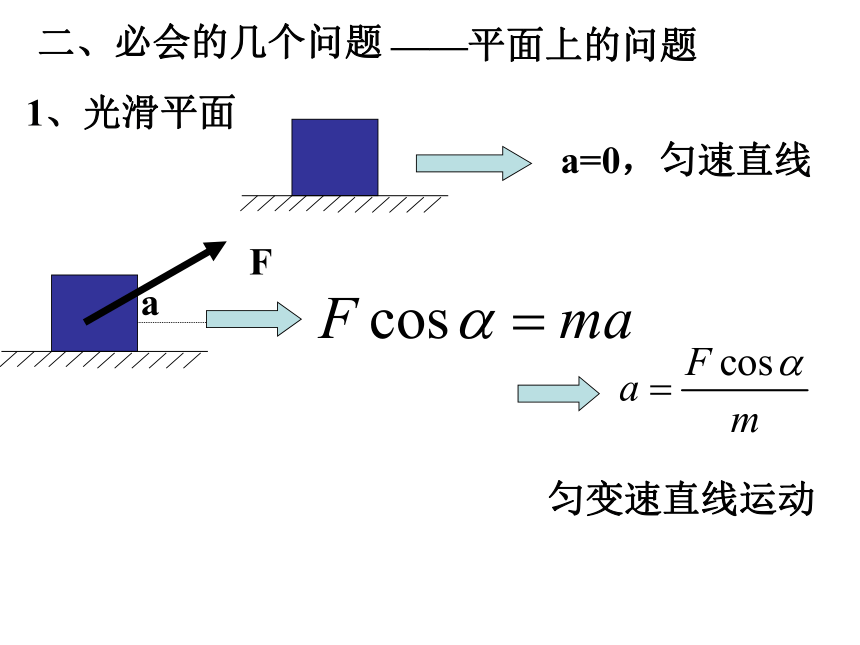
——平面上的问题
1、光滑平面
a=0,匀速直线
匀变速直线运动
二、必会的几个问题
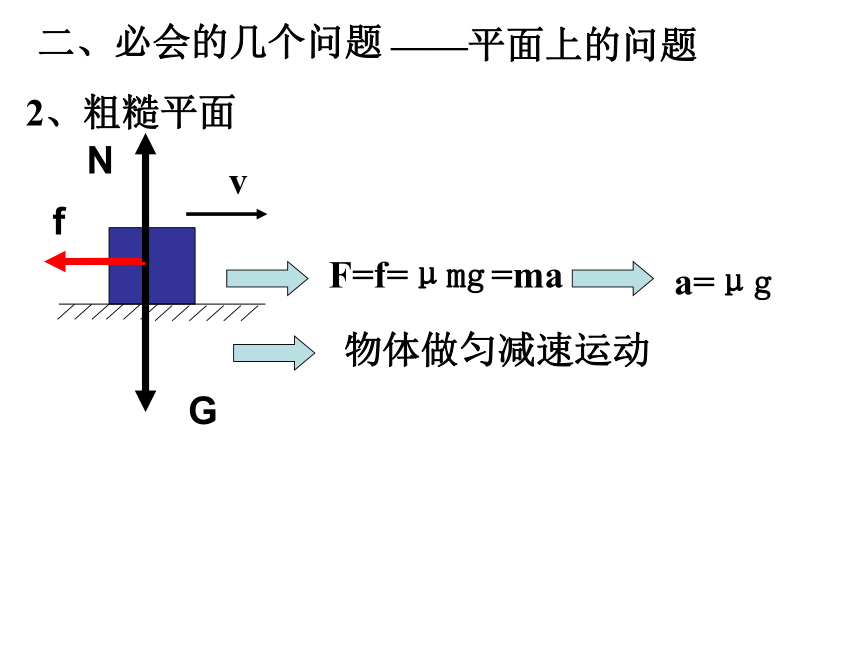
——平面上的问题
2、粗糙平面
F=f=μmg
=ma
a=μg
物体做匀减速运动
二、必会的几个问题
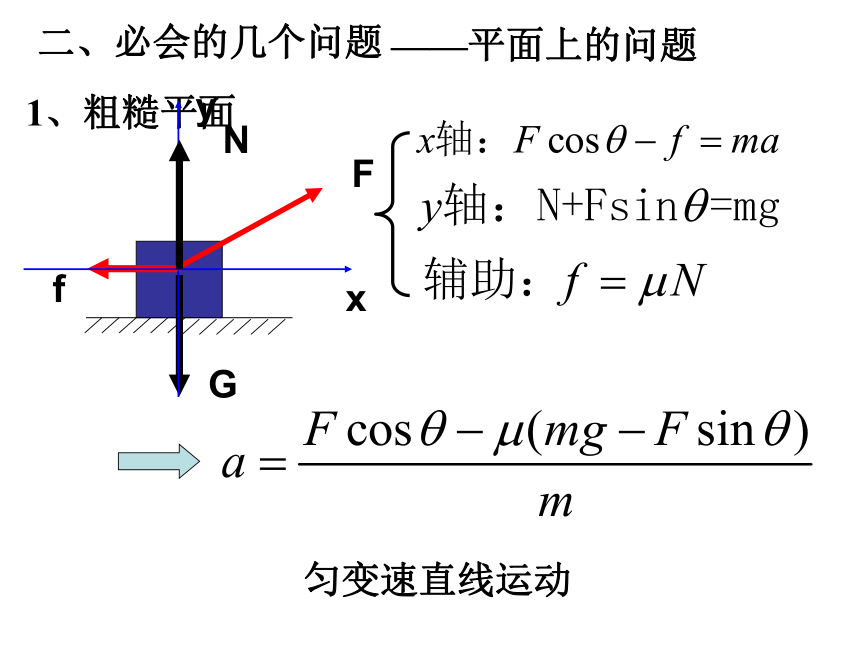
——平面上的问题
1、粗糙平面
匀变速直线运动
例1:如图,质量为2kg的物体静止在水平地面上,物体与水平面间的动摩擦因数为0.2,现对物体施加一个大小F=5N与水平方向成θ=370角的斜向上的拉力(如图),已知:g=10m/s2,求:
(1)若4s后撤去拉力F,则物体还能滑行多远?
(2)物体运动的总时间?
(3)画出物体运动过程中速度—时间图像?
二、必会的几个问题
1、平面上的问题
2、斜面的上的问题
3、竖直方向的问题
二、必会的几个问题
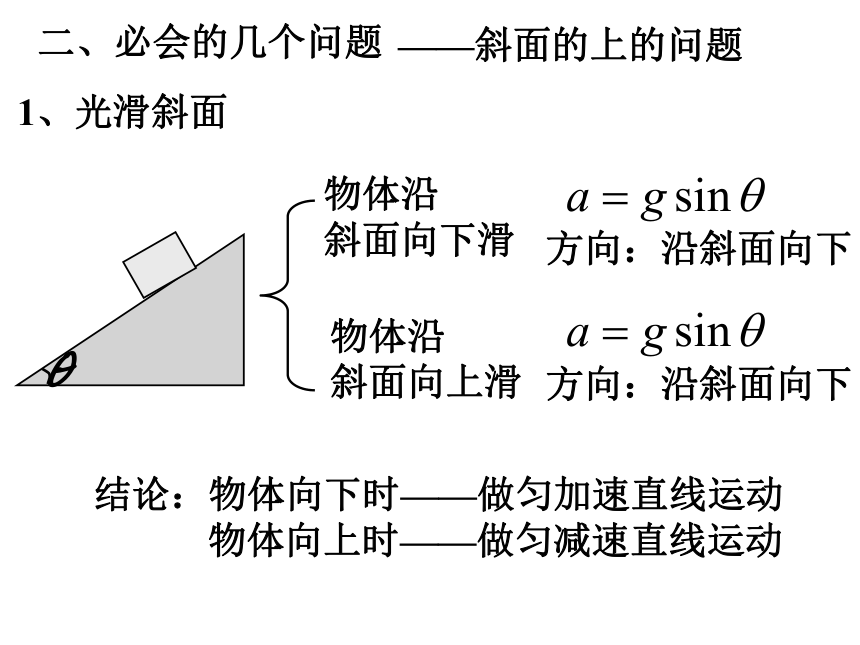
——斜面的上的问题
1、光滑斜面
物体沿
斜面向下滑
物体沿
斜面向上滑
结论:物体向下时——做匀加速直线运动
物体向上时——做匀减速直线运动
方向:沿斜面向下
方向:沿斜面向下
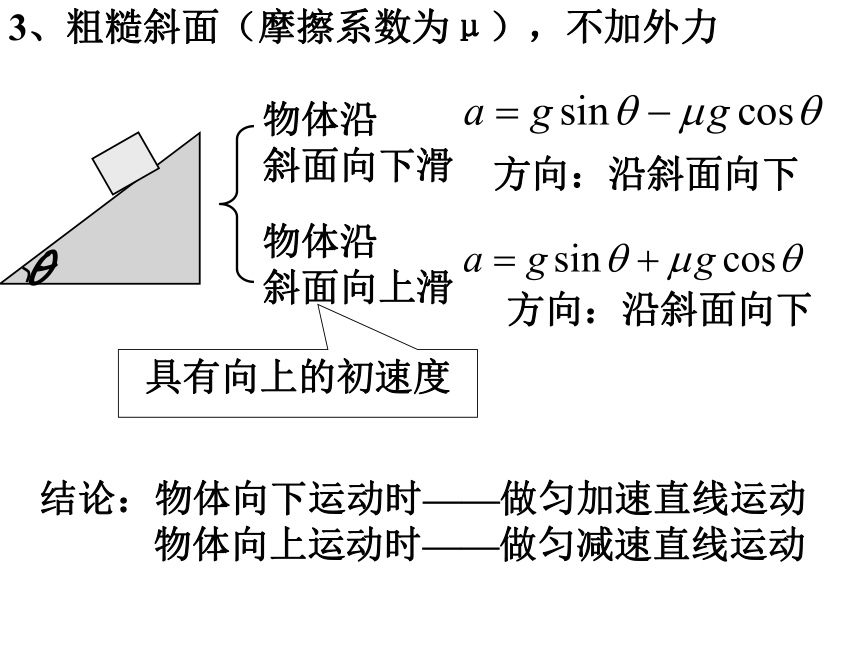
3、粗糙斜面(摩擦系数为μ),不加外力
物体沿
斜面向下滑
物体沿
斜面向上滑
方向:沿斜面向下
结论:物体向下运动时——做匀加速直线运动
物体向上运动时——做匀减速直线运动
具有向上的初速度
方向:沿斜面向下
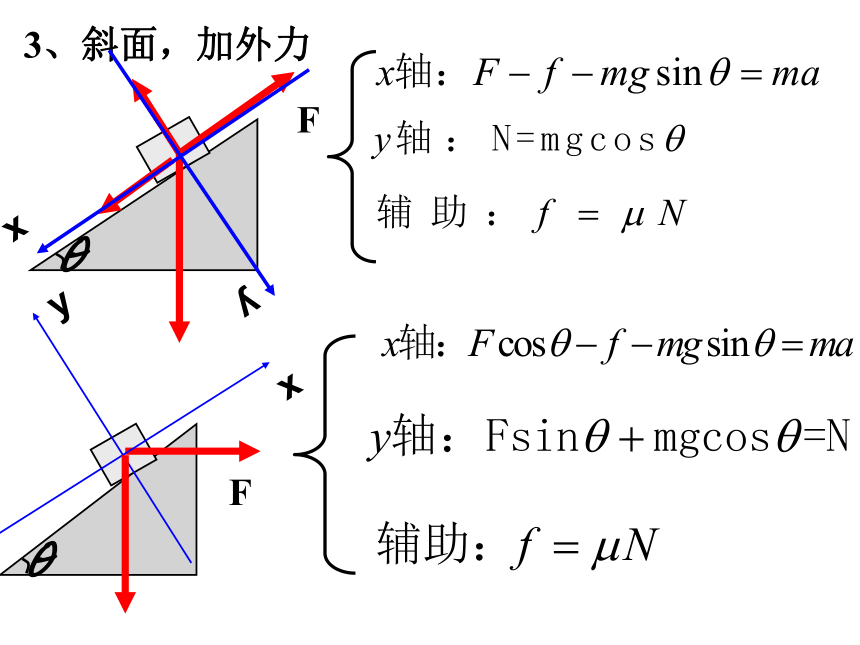
3、斜面,加外力
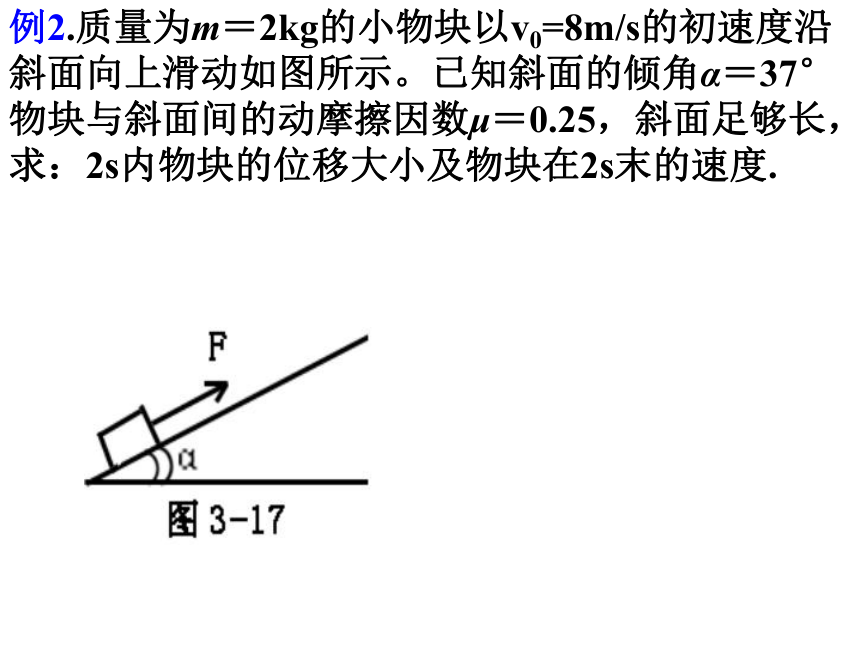
例2.质量为m=2kg的小物块以v0=8m/s的初速度沿
斜面向上滑动如图所示。已知斜面的倾角α=37°
物块与斜面间的动摩擦因数μ=0.25,斜面足够长,
求:2s内物块的位移大小及物块在2s末的速度.
二、必会的几个问题
1、平面上的问题
2、斜面的上的问题
3、竖直方向的问题
二、必会的几个问题
——竖直方向的问题
1、无空气阻力
特点:只受重力
a=g,方向竖直向下
从初速度
角度可分
自由落
体运动
竖直上
抛运动
以向上方向为正方向,竖直向上抛运动是一个加速度为-g的匀减速直线运动。
例3:
从塔上以20m/s的初速度竖直向上抛一个石子,不考虑空气阻力,求5s末石子速度和5s内石子位移。(g=10m/s2)。
V0
以向上方向为正方向。
x正
x
Vt
二、必会的几个问题
——竖直方向的问题
1、有空气阻力,且大小不变
特点:受重力
空气阻力,与速度方向相反
物体向
上运动
物体向
下运动
F合=mg+f=ma
F合=mg-f=ma
a=g+f/m
a=g-f/m
方向向下
方向向下
例4:.将物体竖直上抛,假设运动过程中空气阻力
不变,其速度–时间图象如图所示,则物体所
受的重力和空气阻力之比为( )
A.1:10 B.10:1
C.9:1 D.8:1
t/s
v/(m·s-1)
0
11
-9
1
2
三 、动力学的两类基本问题
1.已知物体的受力情况,要求确定物体的运动情况
处理方法:已知物体的受力情况,可以求出物体的合外力,根据牛顿第二定律可以求出物体的加速度,再利用物体的初始条件(初位置和初速度),根据运动学公式就可以求出物体的位移和速度.也就是确定了物体的运动情况.
2.已知物体的运动情况,要求推断物体的受力情况
处理方法:已知物体的运动情况,由运动学公式求出加速度,再根据牛顿第二定律就可以确定物体所受的合外力,由此推断物体受力情况.
两类问题:
① 已知物体受力的情况,确定物体运动情况。
② 已知物体的运动情况,确定物体受力情况。
解题思路:
牛顿运动定律的应用
加速度a
运动情况
受力情况
加速度a
一般步骤:
(1)确定研究对象;
(2)受力及状态分析;
(3)取正方向,列方程;
(4)统一单位,代值求解;
(5)检验结果.
两类问题:
① 已知物体受力的情况,确定物体运动情况。
② 已知物体的运动情况,确定物体受力情况。
解题思路:
牛顿运动定律的应用
加速度a
运动情况
受力情况
加速度a
质量是2kg,在6.4N的水平拉力作用下
沿水平地面向右运动。物体与地面间
的摩擦力是4.2N.问物体在4 s末的速
度和4 s内发生的位移。
一个静止在水平地面上的物体,
是不是我们熟悉的某种运动呢?
加速度呢?怎么求?
初速度为零
牛顿第二定律
一、研究对象是谁?
二、受几个力的作用?
三、合力沿什么方向?大小是多少?
受力分析
y:Fy合=0
x:Fx合=2.2 N
解:(1)由牛顿第二定律
F合=ma,
可以求出物体的加速度
a=F合/m=(F-f)/m =1.1 m/s2
(2)求出了物体的加速度a,由运动学公式就可以求出4s末的速度
v=at=1.1×4 m/s=4.4 m/s,
4s内发生的位移x.
x=1/2*at2=0.5×1.1×16 m=8.8 m.
除了这类
已知受力求运动
的问题外,
生活中还有另一种问题
也很常见。
“已知受力求运动”解题思路:
力
运动
a
F=ma
分析受力
分析运动
运动学公式
一个滑雪的人,质量是75kg,以
v0=2 m/s的初速度沿山坡匀加速滑下,
山坡的倾角θ=300。在t=5s的时间内
滑下的路程 x=60m。求滑雪人受到的
阻力(包括摩擦和空气)。
受力分析
合力沿什么方向?
合力沿斜面向下。
受力方向复杂,如何求合力?
沿平行于斜面向下和垂直斜面向上为+x,+y轴。
解(1)如图所示建立坐标系,把重力G沿x轴方向和y轴方向进行分解,得到: Gx=mgsinθ,Gy=mgcosθ,
人沿山坡做匀加速运动,由运动学公式:
x=v0t+1/2at2 解出 a=2(x-v0t)/t2, a=4 m/s2
(2)根据牛顿第二定律得:
F阻=Gx-ma=mgsinθ-ma
代入数值得:F阻=67.5 N.
“已知运动求受力”解题思路:
运动
a
F=ma
分析运动
分析受力
运动学公式
力
总结
1.例2中物体受力方向较为复杂,建立平面直角坐
标系后,就可以用Gx和Gy代替G,使解题方便。
2.因为加速度方向就是物体所受合外力的方向,
所以以加速度的方向为正方向,会给分析问题带来
很大方便。
力
运动
a
F=ma
分析受力
分析运动
运动学公式
运动
F=ma
分析运动
分析受力
运动学公式
力
a
练习1:质量为100t的机车从停车场出发,经225m后,速度达到54km/h,此时,司机关闭发动机,让机车进站,机车又行驶125m才停在站上.设运动阻力不变,求机车关闭发动机前所受到的牵引力.
四、简单连结体问题
连结体:两个(或两个以上)物体相互连结参
以运动的系统。
内力与外力:
连结体间的相互作用力叫内力;
外部对连结体的作用力叫外力。
外力
内力
例1:如图所示,质量为2kg 的正方体A和质量为1kg 的正方体B两个物体靠在一起,放在光滑的水平面上,现用水平力F=30N推A,求A对B作用力的大小。
A
四、简单的连接体问题
F
F合 =F =30N
先分析AB整体的受力情况:
B
AB
G
N
F
再分析B的受力情况:
B
GB
NB
FB
FB =mBa=10N
例2:如图所示,质量为2kg 的m1和质量为1kg 的m2两个物体用水平细线连接,放在光滑的水平面上,现用水平拉力F拉m1,使m1 和m2一起沿水平面运动,若细线能承受的最大拉力为8N,求水平拉力F的最大值。
二、简单的连接体问题
F
m2
m1
先分析m2 的受力情况:
G2
N2
T
再分析m1m2整体受力情况:
m1 m2
G
N
F
F =(m1+m2)a=24N
四、简单的连接体问题
小结:
先用整体法求加速度,
1、已知外力求内力:
再用隔离法求内力
先用隔离法求加速度,
2、已知内力求外力:
再用整体法求外力
例与练
1、如图所示,在水平地面上有两个相互接触的物体A和B,它们的质量分别为m1 和m2 ,与地面间的动摩擦因数都是μ,现用水平推力F向右推A,使A、B一起沿地面向前运动,则A对B的作用力为多大?
A
F
B
f =μN=μ(m1+m2)g
先分析AB整体的受力情况:
AB
G
N
F
f
F合 =F-f =F-μ(m1+m2)g
例与练
1、如图所示,在水平地面上有两个相互接触的物体A和B,它们的质量分别为m1 和m2 ,与地面间的动摩擦因数都是μ,现用水平推力F向右推A,使A、B一起沿地面向前运动,则A对B的作用力为多大?
A
F
B
AB
G
N
F
再分析B的受力情况:
B
GB
NB
FB
FB合 =FB-fB=m2a
f
fB
FB =fB+m2a
fB =μNB=μm2g
m2
例与练
2、如图所示,质量为2kg 的m1和质量为1kg 的m2两个物体叠放在一起,放在水平面,m1 与m2、m1与水平面间的动摩擦因数都是0.3,现用水平拉力F拉m1,使m1 和m2一起沿水平面运动,要使m1 和m2之间没有相对滑动,水平拉力F最大为多大?
G2
N2
f2
先分析m2的受力情况:
f2 =μN2=μm2g=3N
f2 =m2a
例与练
3、如图所示,质量为2kg 的m1和质量为1kg 的m2两个物体叠放在一起,放在水平面,m1 与m2、m1与水平面间的动摩擦因数都是0.3,现用水平拉力F拉m1,使m1 和m2一起沿水平面运动,要使m1 和m2之间没有相对滑动,水平拉力F最大为多大?
4.如图所示,在光滑的水平面上,有等质量的五个物体,每个物体的质量为m.若用水平推力F推1号物体,求:
(1)它们的加速度是多少?
(2)2、3号物体间的压力为多少?
解:因各个物体的加速度相同,可以五个物体整体为研究对象求出整体的加速度.再以3、4、5号物体为研究对象求出2、3号物体间的压力.
对整体 F=5ma
对3、4、5号物体 T=3ma
得 a=F/5m; T=3F/5
五、传输带问题
六、与图像结合的问题
七、临界问题
八、瞬时问题
五、传送带问题:
1、如图所示,传送带保持10m/s的速度运动,现将一质量为0.5kg的小物体从传送带左端放上,设物体与皮带间动摩擦因数为0.1,传送带两端水平距离为2.5m,则物体从左端运动到右端所经历的时间为?
五、传送带问题:
2、如图所示,传送带保持1m/s的速度运动,现将一质量为0.5kg的小物体从传送带左端放上,设物体与皮带间动摩擦因数为0.1,传送带两端水平距离为2.5m,则物体从左端运动到右端所经历的时间为?
24.(2006年高考题19分)一水平的浅色长传送带上放置一煤块(可视为质点),煤块与传送带之间的动摩擦因数为μ。初始时,传送带与煤块都是静止的。现让传送带以恒定的加速度a0开始运动,当其速度达到v0后,便以此速度做匀速运动。经过一段时间,煤块在传送带上留下了一段黑色痕迹后,煤块相对于传送带不再滑动。求此黑色痕迹的长度。
例3、如图所示,传送带与地面的倾角370,从
A到B长度为16m,传送带以10 m /s的速度运
行。在传送带上端A无初速地放一个质量为
0.5 kg的物体,它与传送带之间的 μ=0.5,
求物体从A到B的时间 ?
五、传输带问题
六、与图像结合的问题
七、临界问题
八、瞬时问题
1. 如图所示,是一辆汽车在两站间行驶的速度图像,汽车所受到的阻力大小为2000N不变,且BC段的牵引力为零,已知汽车的质量为4000kg,则汽车在BC段的加速度大小为 , OA段汽车的牵引力大小为 。
2、 物体A、B都静止在同一水平面上,它们的质量分别是mA和mB,与水平面之间的动摩擦因数分别为μA和μB。用平行于水平面的力F分别拉物体A、B,得到加速度a和拉力F的关系图象分别如图中A、B所示。利用图象求出A、B两物体与水平面之间动摩擦因数μA和μB的数值。
二.力与运动关系的定性分析
一.动力学的两类基本问题
四.牛顿第二定律的瞬时性
三.正交分解法
五.临界问题
六.皮带问题分析
七.连接体问题
例1.如图所示,当剪断AB、OB舜时,
求两图中小球的加速度。
[例2] 如图所示,A、B两物体的质量分别为M和m,中间用轻弹簧相连,物体与水平面间的摩擦因数为μ,在水平拉力作用下,A、B一起以加速度a向右作匀加速直线运动。试求突然撤去拉力的瞬间,两物体的加速度各为多大。
答案:aA=a ,aB=Ma+μ(M+m)g/m
[练习] 一块木板上叠放着两个物体(如图所示),它们的质量关系为M=2m,中间用一轻弹簧联结,并处于静止状态。突然抽去木板,此时上、下两物体的加速度各为( )
A、g, 2g; B、0,g
C、0,2g; D、0,1.5g。
例4:一个质量为0.2kg的小球用细绳吊在倾角为?=35?的斜面顶端如右图示,斜面静止时,球紧靠在斜面上,绳与斜面平行,不计摩擦,当斜面以10m/s2的加速度向右运动时,求绳子的拉力及斜面对小球的弹力.
解析:用极限法把加速度a推到两个极端来分析,当a较小时( a ?0),小球受到三个力(重力、绳索的拉力和斜面支持力)作用,此时绳平行于斜面;当a较大时(足够大),小球将“飞离”斜面,此时绳与水平方向夹角未知.那么a=10m/s2向右时,究竟是上述两种情况中的哪一种?
解题时必须先求出小球离开斜面的临界值然后才能确定.
令小球处在离开斜面的临界状态(N刚好为零)时,斜面向右的加速度为a0,此时小球受力分析如下图所示.
所以小球会离开斜面,受力如下图
一、牛顿第二定律的内容:
F=ma
力
分力还是合力?
加速度
同一物体,共同的质量
如何求得?
二、必会的几个问题
1、平面上的问题
2、斜面的上的问题
3、竖直方向的问题
二、必会的几个问题
——平面上的问题
1、光滑平面
a=0,匀速直线
匀变速直线运动
二、必会的几个问题
——平面上的问题
2、粗糙平面
F=f=μmg
=ma
a=μg
物体做匀减速运动
二、必会的几个问题
——平面上的问题
1、粗糙平面
匀变速直线运动
例1:如图,质量为2kg的物体静止在水平地面上,物体与水平面间的动摩擦因数为0.2,现对物体施加一个大小F=5N与水平方向成θ=370角的斜向上的拉力(如图),已知:g=10m/s2,求:
(1)若4s后撤去拉力F,则物体还能滑行多远?
(2)物体运动的总时间?
(3)画出物体运动过程中速度—时间图像?
二、必会的几个问题
1、平面上的问题
2、斜面的上的问题
3、竖直方向的问题
二、必会的几个问题
——斜面的上的问题
1、光滑斜面
物体沿
斜面向下滑
物体沿
斜面向上滑
结论:物体向下时——做匀加速直线运动
物体向上时——做匀减速直线运动
方向:沿斜面向下
方向:沿斜面向下
3、粗糙斜面(摩擦系数为μ),不加外力
物体沿
斜面向下滑
物体沿
斜面向上滑
方向:沿斜面向下
结论:物体向下运动时——做匀加速直线运动
物体向上运动时——做匀减速直线运动
具有向上的初速度
方向:沿斜面向下
3、斜面,加外力
例2.质量为m=2kg的小物块以v0=8m/s的初速度沿
斜面向上滑动如图所示。已知斜面的倾角α=37°
物块与斜面间的动摩擦因数μ=0.25,斜面足够长,
求:2s内物块的位移大小及物块在2s末的速度.
二、必会的几个问题
1、平面上的问题
2、斜面的上的问题
3、竖直方向的问题
二、必会的几个问题
——竖直方向的问题
1、无空气阻力
特点:只受重力
a=g,方向竖直向下
从初速度
角度可分
自由落
体运动
竖直上
抛运动
以向上方向为正方向,竖直向上抛运动是一个加速度为-g的匀减速直线运动。
例3:
从塔上以20m/s的初速度竖直向上抛一个石子,不考虑空气阻力,求5s末石子速度和5s内石子位移。(g=10m/s2)。
V0
以向上方向为正方向。
x正
x
Vt
二、必会的几个问题
——竖直方向的问题
1、有空气阻力,且大小不变
特点:受重力
空气阻力,与速度方向相反
物体向
上运动
物体向
下运动
F合=mg+f=ma
F合=mg-f=ma
a=g+f/m
a=g-f/m
方向向下
方向向下
例4:.将物体竖直上抛,假设运动过程中空气阻力
不变,其速度–时间图象如图所示,则物体所
受的重力和空气阻力之比为( )
A.1:10 B.10:1
C.9:1 D.8:1
t/s
v/(m·s-1)
0
11
-9
1
2
三 、动力学的两类基本问题
1.已知物体的受力情况,要求确定物体的运动情况
处理方法:已知物体的受力情况,可以求出物体的合外力,根据牛顿第二定律可以求出物体的加速度,再利用物体的初始条件(初位置和初速度),根据运动学公式就可以求出物体的位移和速度.也就是确定了物体的运动情况.
2.已知物体的运动情况,要求推断物体的受力情况
处理方法:已知物体的运动情况,由运动学公式求出加速度,再根据牛顿第二定律就可以确定物体所受的合外力,由此推断物体受力情况.
两类问题:
① 已知物体受力的情况,确定物体运动情况。
② 已知物体的运动情况,确定物体受力情况。
解题思路:
牛顿运动定律的应用
加速度a
运动情况
受力情况
加速度a
一般步骤:
(1)确定研究对象;
(2)受力及状态分析;
(3)取正方向,列方程;
(4)统一单位,代值求解;
(5)检验结果.
两类问题:
① 已知物体受力的情况,确定物体运动情况。
② 已知物体的运动情况,确定物体受力情况。
解题思路:
牛顿运动定律的应用
加速度a
运动情况
受力情况
加速度a
质量是2kg,在6.4N的水平拉力作用下
沿水平地面向右运动。物体与地面间
的摩擦力是4.2N.问物体在4 s末的速
度和4 s内发生的位移。
一个静止在水平地面上的物体,
是不是我们熟悉的某种运动呢?
加速度呢?怎么求?
初速度为零
牛顿第二定律
一、研究对象是谁?
二、受几个力的作用?
三、合力沿什么方向?大小是多少?
受力分析
y:Fy合=0
x:Fx合=2.2 N
解:(1)由牛顿第二定律
F合=ma,
可以求出物体的加速度
a=F合/m=(F-f)/m =1.1 m/s2
(2)求出了物体的加速度a,由运动学公式就可以求出4s末的速度
v=at=1.1×4 m/s=4.4 m/s,
4s内发生的位移x.
x=1/2*at2=0.5×1.1×16 m=8.8 m.
除了这类
已知受力求运动
的问题外,
生活中还有另一种问题
也很常见。
“已知受力求运动”解题思路:
力
运动
a
F=ma
分析受力
分析运动
运动学公式
一个滑雪的人,质量是75kg,以
v0=2 m/s的初速度沿山坡匀加速滑下,
山坡的倾角θ=300。在t=5s的时间内
滑下的路程 x=60m。求滑雪人受到的
阻力(包括摩擦和空气)。
受力分析
合力沿什么方向?
合力沿斜面向下。
受力方向复杂,如何求合力?
沿平行于斜面向下和垂直斜面向上为+x,+y轴。
解(1)如图所示建立坐标系,把重力G沿x轴方向和y轴方向进行分解,得到: Gx=mgsinθ,Gy=mgcosθ,
人沿山坡做匀加速运动,由运动学公式:
x=v0t+1/2at2 解出 a=2(x-v0t)/t2, a=4 m/s2
(2)根据牛顿第二定律得:
F阻=Gx-ma=mgsinθ-ma
代入数值得:F阻=67.5 N.
“已知运动求受力”解题思路:
运动
a
F=ma
分析运动
分析受力
运动学公式
力
总结
1.例2中物体受力方向较为复杂,建立平面直角坐
标系后,就可以用Gx和Gy代替G,使解题方便。
2.因为加速度方向就是物体所受合外力的方向,
所以以加速度的方向为正方向,会给分析问题带来
很大方便。
力
运动
a
F=ma
分析受力
分析运动
运动学公式
运动
F=ma
分析运动
分析受力
运动学公式
力
a
练习1:质量为100t的机车从停车场出发,经225m后,速度达到54km/h,此时,司机关闭发动机,让机车进站,机车又行驶125m才停在站上.设运动阻力不变,求机车关闭发动机前所受到的牵引力.
四、简单连结体问题
连结体:两个(或两个以上)物体相互连结参
以运动的系统。
内力与外力:
连结体间的相互作用力叫内力;
外部对连结体的作用力叫外力。
外力
内力
例1:如图所示,质量为2kg 的正方体A和质量为1kg 的正方体B两个物体靠在一起,放在光滑的水平面上,现用水平力F=30N推A,求A对B作用力的大小。
A
四、简单的连接体问题
F
F合 =F =30N
先分析AB整体的受力情况:
B
AB
G
N
F
再分析B的受力情况:
B
GB
NB
FB
FB =mBa=10N
例2:如图所示,质量为2kg 的m1和质量为1kg 的m2两个物体用水平细线连接,放在光滑的水平面上,现用水平拉力F拉m1,使m1 和m2一起沿水平面运动,若细线能承受的最大拉力为8N,求水平拉力F的最大值。
二、简单的连接体问题
F
m2
m1
先分析m2 的受力情况:
G2
N2
T
再分析m1m2整体受力情况:
m1 m2
G
N
F
F =(m1+m2)a=24N
四、简单的连接体问题
小结:
先用整体法求加速度,
1、已知外力求内力:
再用隔离法求内力
先用隔离法求加速度,
2、已知内力求外力:
再用整体法求外力
例与练
1、如图所示,在水平地面上有两个相互接触的物体A和B,它们的质量分别为m1 和m2 ,与地面间的动摩擦因数都是μ,现用水平推力F向右推A,使A、B一起沿地面向前运动,则A对B的作用力为多大?
A
F
B
f =μN=μ(m1+m2)g
先分析AB整体的受力情况:
AB
G
N
F
f
F合 =F-f =F-μ(m1+m2)g
例与练
1、如图所示,在水平地面上有两个相互接触的物体A和B,它们的质量分别为m1 和m2 ,与地面间的动摩擦因数都是μ,现用水平推力F向右推A,使A、B一起沿地面向前运动,则A对B的作用力为多大?
A
F
B
AB
G
N
F
再分析B的受力情况:
B
GB
NB
FB
FB合 =FB-fB=m2a
f
fB
FB =fB+m2a
fB =μNB=μm2g
m2
例与练
2、如图所示,质量为2kg 的m1和质量为1kg 的m2两个物体叠放在一起,放在水平面,m1 与m2、m1与水平面间的动摩擦因数都是0.3,现用水平拉力F拉m1,使m1 和m2一起沿水平面运动,要使m1 和m2之间没有相对滑动,水平拉力F最大为多大?
G2
N2
f2
先分析m2的受力情况:
f2 =μN2=μm2g=3N
f2 =m2a
例与练
3、如图所示,质量为2kg 的m1和质量为1kg 的m2两个物体叠放在一起,放在水平面,m1 与m2、m1与水平面间的动摩擦因数都是0.3,现用水平拉力F拉m1,使m1 和m2一起沿水平面运动,要使m1 和m2之间没有相对滑动,水平拉力F最大为多大?
4.如图所示,在光滑的水平面上,有等质量的五个物体,每个物体的质量为m.若用水平推力F推1号物体,求:
(1)它们的加速度是多少?
(2)2、3号物体间的压力为多少?
解:因各个物体的加速度相同,可以五个物体整体为研究对象求出整体的加速度.再以3、4、5号物体为研究对象求出2、3号物体间的压力.
对整体 F=5ma
对3、4、5号物体 T=3ma
得 a=F/5m; T=3F/5
五、传输带问题
六、与图像结合的问题
七、临界问题
八、瞬时问题
五、传送带问题:
1、如图所示,传送带保持10m/s的速度运动,现将一质量为0.5kg的小物体从传送带左端放上,设物体与皮带间动摩擦因数为0.1,传送带两端水平距离为2.5m,则物体从左端运动到右端所经历的时间为?
五、传送带问题:
2、如图所示,传送带保持1m/s的速度运动,现将一质量为0.5kg的小物体从传送带左端放上,设物体与皮带间动摩擦因数为0.1,传送带两端水平距离为2.5m,则物体从左端运动到右端所经历的时间为?
24.(2006年高考题19分)一水平的浅色长传送带上放置一煤块(可视为质点),煤块与传送带之间的动摩擦因数为μ。初始时,传送带与煤块都是静止的。现让传送带以恒定的加速度a0开始运动,当其速度达到v0后,便以此速度做匀速运动。经过一段时间,煤块在传送带上留下了一段黑色痕迹后,煤块相对于传送带不再滑动。求此黑色痕迹的长度。
例3、如图所示,传送带与地面的倾角370,从
A到B长度为16m,传送带以10 m /s的速度运
行。在传送带上端A无初速地放一个质量为
0.5 kg的物体,它与传送带之间的 μ=0.5,
求物体从A到B的时间 ?
五、传输带问题
六、与图像结合的问题
七、临界问题
八、瞬时问题
1. 如图所示,是一辆汽车在两站间行驶的速度图像,汽车所受到的阻力大小为2000N不变,且BC段的牵引力为零,已知汽车的质量为4000kg,则汽车在BC段的加速度大小为 , OA段汽车的牵引力大小为 。
2、 物体A、B都静止在同一水平面上,它们的质量分别是mA和mB,与水平面之间的动摩擦因数分别为μA和μB。用平行于水平面的力F分别拉物体A、B,得到加速度a和拉力F的关系图象分别如图中A、B所示。利用图象求出A、B两物体与水平面之间动摩擦因数μA和μB的数值。
二.力与运动关系的定性分析
一.动力学的两类基本问题
四.牛顿第二定律的瞬时性
三.正交分解法
五.临界问题
六.皮带问题分析
七.连接体问题
例1.如图所示,当剪断AB、OB舜时,
求两图中小球的加速度。
[例2] 如图所示,A、B两物体的质量分别为M和m,中间用轻弹簧相连,物体与水平面间的摩擦因数为μ,在水平拉力作用下,A、B一起以加速度a向右作匀加速直线运动。试求突然撤去拉力的瞬间,两物体的加速度各为多大。
答案:aA=a ,aB=Ma+μ(M+m)g/m
[练习] 一块木板上叠放着两个物体(如图所示),它们的质量关系为M=2m,中间用一轻弹簧联结,并处于静止状态。突然抽去木板,此时上、下两物体的加速度各为( )
A、g, 2g; B、0,g
C、0,2g; D、0,1.5g。
例4:一个质量为0.2kg的小球用细绳吊在倾角为?=35?的斜面顶端如右图示,斜面静止时,球紧靠在斜面上,绳与斜面平行,不计摩擦,当斜面以10m/s2的加速度向右运动时,求绳子的拉力及斜面对小球的弹力.
解析:用极限法把加速度a推到两个极端来分析,当a较小时( a ?0),小球受到三个力(重力、绳索的拉力和斜面支持力)作用,此时绳平行于斜面;当a较大时(足够大),小球将“飞离”斜面,此时绳与水平方向夹角未知.那么a=10m/s2向右时,究竟是上述两种情况中的哪一种?
解题时必须先求出小球离开斜面的临界值然后才能确定.
令小球处在离开斜面的临界状态(N刚好为零)时,斜面向右的加速度为a0,此时小球受力分析如下图所示.
所以小球会离开斜面,受力如下图
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
