人教版五年级下册数学【名师课件】第九单元 期末总复习 第3--4课时 图形与几何(共36张PPT)
文档属性
| 名称 | 人教版五年级下册数学【名师课件】第九单元 期末总复习 第3--4课时 图形与几何(共36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 21.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-05 16:48:20 | ||
图片预览











文档简介
(共36张PPT)
R·五年级下册
第3课时 图形与几何(1)
学习目标
1.通过观察,能正确辨认从正面、侧面、上面观察到的一组立体图形的位置关系和形状。
2.理解长方体、正方体的有关知识,使学生会区分体积和表面积两个概念并掌握其内在的联系,能灵活运用。
3.进一步认识图形的旋转,能在方格纸上把简单的图形旋转90°。
一、复习导入
这学期我们学了哪些和“图形与几何”有关的内容?在哪个单元学的呢?
思考
第一单元学习了观察物体。
第三单元学习了长方体和正方体。
第五单元学习了图形的运动。
你学到了什么,说说你的收获吧!
我认识了长方体和正方体。
我会画旋转后的图形样子。
我探究出了体积公式的计算方法……
大家说得不够完善,今天我们就来系统地复习一下。
二、知识梳理
问题
观察物体要注意什么?有什么规律?
根据从一个方向看到的平面图形摆出的立体图形不一定相同。
1.
2.
根据从三个方向看到的平面图形确定的立体图形的形状一定相同。
你是这样想的吗?
长方体和正方体有哪些相同点?有哪些不同点?
长方体 正方体
相同点 6个面、12条棱、8个顶点
不同点 6个面都是长方形(有时相对的两个面是正方形),相对面完全相同。 6个面都是正方形,
6个面完全相同。
相对棱的长度相等 12条棱长度都相等
正方体是特殊的长方体。
问
正方体和长方体的表面积的计算公式是什么?
正方体的表面积=边长×边长×6,用字母表示是S=6a2;长方体的表面积=(长×宽+长×高+宽×高)×2,用字母表示是S=(ab+ah+bh)×2。
问
长方体和正方体体积的计算公式是什么?
长方体的体积=长×宽×高,用字母表示是V=abh;正方体的体积=棱长×棱长×棱长,用字母表示是V=a3。
什么运动是旋转?旋转有什么特点?
思考
图形的旋转是图形上的每一点在平面上绕某个旋转中心旋转一定角度的位置移动。
你能举例说明吗?
旋转前后图形的大小和形状没有改变;两组对应点分别与旋转中心的连线所成的角相等,都等于旋转角;旋转中心是唯一不动的点。
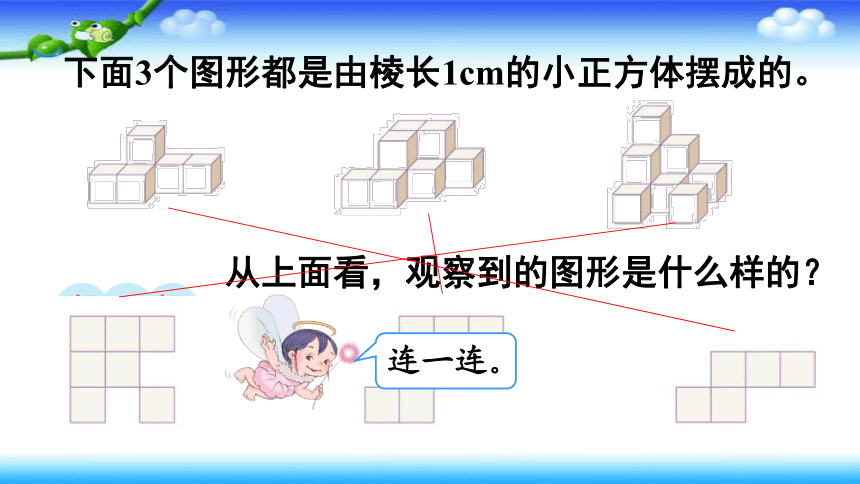
下面3个图形都是由棱长1cm的小正方体摆成的。
从上面看,观察到的图形是什么样的?
连一连。
下面3个图形都是由棱长1cm的小正方体摆成的。
①、②、③的体积分别是多少?①的体积是③的体积的几分之几?
问题
你是怎么想的?
数出小正方体的个数就可以了。
棱长为1 cm的小正方体的体积是1 cm3。
6 cm3
10 cm3
11 cm3
①的体积是③的体积的 。
如果要把①、②、③分别继续补搭成一个大正方体,每个图形至少还需要多少个小正方体?
怎样做比较简便?
要补成大正方体,则图形的正面、侧面和上面的都是正方形,且小正方体个数都得一样多。
图形①:4×4×4-6=58(个)
图形②:4×4×4-10=54(个)
图形③:3×3×3-11=16(个)
左图怎样变换可以得到右图呢?
O
左边图形以O点为旋转中心,分别顺时针旋转90°,180°,270°,就可得到右边的图形。
图中绿色部分占整个图案的几分之几?红色部分占整个图案的几分之几?
问题
绿色部分所占方格数:
4
红色部分所占方格数:
4×2=8
绿色部分占整个图案:
红色部分占整个图案:
三、巩固深化
1.观察右边的图形,填一填。
(1) 图形①绕O点 方向旋转
90°到图形 所在的位置;
(2) 图形②绕O点 方向旋转
90°到图形 所在的位置;
(3)图形③绕O点 方向旋转90°到图形 所
在的位置。
顺时针
②
顺时针
③
顺时针
④
2.填空题。
(1)一个棱长是2m的正方体,它的表面积是( )m2,体积是( )m3。
(2)1.36L= ( )cm3 3.25小时= ( )分钟
(3)一个正方体纸盒的棱长总和是36cm,它的表面积是( )cm2,体积是( )cm3。
(4)一个正方体的棱长扩大到原来的3倍,它的体积就扩大到原来的( )倍。
24
8
1360
195
54
27
27
3.一个装满沙子的长方体沙坑长7米、宽3米、深0.8米,每立方米沙子重1400千克,这个沙坑里共装沙子多少吨?
解答:
7×3×0.8×1400÷1000
=23.52(吨)
答:这个沙坑里共装沙子23.52吨。
四、课堂小结
旋转的意义、性质和特征。
1.
2.
五、课后作业
1.课本P119,第11题;
2.完成练习册本课时的习题。
R·五年级下册
第4课时 图形与几何(2)
学习目标
1. 进一步提高学生观察立体图形的能力。把握立体图形的特点。
2.进一步掌握旋转图形的特点,培养学生动手能力。
3. 提高学生运用长方体正方体表面积和体积知识解决实际问题的能力。
一、复习导入
这是小明从正面看到的图形,如果用6个同样的小正方体可以怎样摆呢?
思考
自己想一想,画一画。
今天我们继续复习图形与几何的内容。
二、知识梳理
问题
你能摆出这个物体的立体图形吗?
从正面看
从上面看
从左面看
想一想,该怎么做呢?
从正面看
有上下两层,左边两层,右边一层。
有上下两层,左边一层,右边两层。
从上面看
能确定什么?
能确定什么?
从左面看
第一层有4个小正方体。
能确定什么?
现在你能画出这个物体的立体图形了吗?
小
结
仅根据从一个或两个方向看到的图形,不能确定立体图形的形状。
从正面看
从上面看
从左面看
逆
风车绕点O( )
时针旋转 °。
风车绕点O( )
时针旋转 °。
逆
90
90
描述旋转时要说清所绕的点、旋转的方向和角度。
以点A为旋转中心把下图逆时针旋转90°。
问题
确定原图形的其他关键点是哪几个?
确定原图形的其他关键点是B、C、D。
怎么画呢?
过点A分别作AC,AB的垂线,在AC的垂线上找到点C的对应点C′,使AC′=AC;
1.
2.
在AB的垂线上找到点B的对应点B′,使AB′=
AB。
3.
在过点A与AD垂线上找到点D的对应点D′,使点A和点D′之间也是4小格。
4.
顺次连接点A、点B′、点D′、点C′,即可得到旋转后的图形。
C′
B′
D′
一个长方体的底面周长是28cm,高是4cm。这个长方体的棱长总长是多少?
问题
长方体有多少条棱呢?
长方体的对应的棱有什么关系呢?
底面周长等于什么?
长方体有12条棱,相对的棱的长度相等。
相交于同一顶点的三条棱的长度分别是长方体的长、宽、高。
解答:
28×2+4×4=56+16=72(cm)
答:这个长方体的棱长总长是72cm。
底面周长=(长+宽)×2。
三、巩固深化
1.下列运动属于什么现象,填一填。
①电梯的上、下,属于( )现象。
②车轮的转动,属于( )现象。
③观光缆车的移动,属于( )现象。
④直升机螺旋桨的转动,属于( )现象。
平移
旋转
平移
旋转
2.有一个长方体,底面是一个正方形,高18cm,侧面展开正好是一个正方形。这个长方体的体积是( ) cm?。
18cm
18cm
18cm
364.5
18÷4=4.5(cm)
4.5×4.5×18
=20.25×18
=364.5(cm?)
先根据题意画图。
3.分别求出下面长方体、正方体的表面积和体积
(单位:cm)
7.5×4×4+42×2=152(cm2)
4×4×7.5=120(cm3)
1.52×6=13.5(cm2)
1.53=3.375(cm3)
四、课堂小结
观察物体
1.
2.
3.
旋转的特征和性质
长方体、正方体的特征和性质
五、课后作业
1.课本P120,第13、14题;
2.完成练习册本课时的习题。
R·五年级下册
第3课时 图形与几何(1)
学习目标
1.通过观察,能正确辨认从正面、侧面、上面观察到的一组立体图形的位置关系和形状。
2.理解长方体、正方体的有关知识,使学生会区分体积和表面积两个概念并掌握其内在的联系,能灵活运用。
3.进一步认识图形的旋转,能在方格纸上把简单的图形旋转90°。
一、复习导入
这学期我们学了哪些和“图形与几何”有关的内容?在哪个单元学的呢?
思考
第一单元学习了观察物体。
第三单元学习了长方体和正方体。
第五单元学习了图形的运动。
你学到了什么,说说你的收获吧!
我认识了长方体和正方体。
我会画旋转后的图形样子。
我探究出了体积公式的计算方法……
大家说得不够完善,今天我们就来系统地复习一下。
二、知识梳理
问题
观察物体要注意什么?有什么规律?
根据从一个方向看到的平面图形摆出的立体图形不一定相同。
1.
2.
根据从三个方向看到的平面图形确定的立体图形的形状一定相同。
你是这样想的吗?
长方体和正方体有哪些相同点?有哪些不同点?
长方体 正方体
相同点 6个面、12条棱、8个顶点
不同点 6个面都是长方形(有时相对的两个面是正方形),相对面完全相同。 6个面都是正方形,
6个面完全相同。
相对棱的长度相等 12条棱长度都相等
正方体是特殊的长方体。
问
正方体和长方体的表面积的计算公式是什么?
正方体的表面积=边长×边长×6,用字母表示是S=6a2;长方体的表面积=(长×宽+长×高+宽×高)×2,用字母表示是S=(ab+ah+bh)×2。
问
长方体和正方体体积的计算公式是什么?
长方体的体积=长×宽×高,用字母表示是V=abh;正方体的体积=棱长×棱长×棱长,用字母表示是V=a3。
什么运动是旋转?旋转有什么特点?
思考
图形的旋转是图形上的每一点在平面上绕某个旋转中心旋转一定角度的位置移动。
你能举例说明吗?
旋转前后图形的大小和形状没有改变;两组对应点分别与旋转中心的连线所成的角相等,都等于旋转角;旋转中心是唯一不动的点。
下面3个图形都是由棱长1cm的小正方体摆成的。
从上面看,观察到的图形是什么样的?
连一连。
下面3个图形都是由棱长1cm的小正方体摆成的。
①、②、③的体积分别是多少?①的体积是③的体积的几分之几?
问题
你是怎么想的?
数出小正方体的个数就可以了。
棱长为1 cm的小正方体的体积是1 cm3。
6 cm3
10 cm3
11 cm3
①的体积是③的体积的 。
如果要把①、②、③分别继续补搭成一个大正方体,每个图形至少还需要多少个小正方体?
怎样做比较简便?
要补成大正方体,则图形的正面、侧面和上面的都是正方形,且小正方体个数都得一样多。
图形①:4×4×4-6=58(个)
图形②:4×4×4-10=54(个)
图形③:3×3×3-11=16(个)
左图怎样变换可以得到右图呢?
O
左边图形以O点为旋转中心,分别顺时针旋转90°,180°,270°,就可得到右边的图形。
图中绿色部分占整个图案的几分之几?红色部分占整个图案的几分之几?
问题
绿色部分所占方格数:
4
红色部分所占方格数:
4×2=8
绿色部分占整个图案:
红色部分占整个图案:
三、巩固深化
1.观察右边的图形,填一填。
(1) 图形①绕O点 方向旋转
90°到图形 所在的位置;
(2) 图形②绕O点 方向旋转
90°到图形 所在的位置;
(3)图形③绕O点 方向旋转90°到图形 所
在的位置。
顺时针
②
顺时针
③
顺时针
④
2.填空题。
(1)一个棱长是2m的正方体,它的表面积是( )m2,体积是( )m3。
(2)1.36L= ( )cm3 3.25小时= ( )分钟
(3)一个正方体纸盒的棱长总和是36cm,它的表面积是( )cm2,体积是( )cm3。
(4)一个正方体的棱长扩大到原来的3倍,它的体积就扩大到原来的( )倍。
24
8
1360
195
54
27
27
3.一个装满沙子的长方体沙坑长7米、宽3米、深0.8米,每立方米沙子重1400千克,这个沙坑里共装沙子多少吨?
解答:
7×3×0.8×1400÷1000
=23.52(吨)
答:这个沙坑里共装沙子23.52吨。
四、课堂小结
旋转的意义、性质和特征。
1.
2.
五、课后作业
1.课本P119,第11题;
2.完成练习册本课时的习题。
R·五年级下册
第4课时 图形与几何(2)
学习目标
1. 进一步提高学生观察立体图形的能力。把握立体图形的特点。
2.进一步掌握旋转图形的特点,培养学生动手能力。
3. 提高学生运用长方体正方体表面积和体积知识解决实际问题的能力。
一、复习导入
这是小明从正面看到的图形,如果用6个同样的小正方体可以怎样摆呢?
思考
自己想一想,画一画。
今天我们继续复习图形与几何的内容。
二、知识梳理
问题
你能摆出这个物体的立体图形吗?
从正面看
从上面看
从左面看
想一想,该怎么做呢?
从正面看
有上下两层,左边两层,右边一层。
有上下两层,左边一层,右边两层。
从上面看
能确定什么?
能确定什么?
从左面看
第一层有4个小正方体。
能确定什么?
现在你能画出这个物体的立体图形了吗?
小
结
仅根据从一个或两个方向看到的图形,不能确定立体图形的形状。
从正面看
从上面看
从左面看
逆
风车绕点O( )
时针旋转 °。
风车绕点O( )
时针旋转 °。
逆
90
90
描述旋转时要说清所绕的点、旋转的方向和角度。
以点A为旋转中心把下图逆时针旋转90°。
问题
确定原图形的其他关键点是哪几个?
确定原图形的其他关键点是B、C、D。
怎么画呢?
过点A分别作AC,AB的垂线,在AC的垂线上找到点C的对应点C′,使AC′=AC;
1.
2.
在AB的垂线上找到点B的对应点B′,使AB′=
AB。
3.
在过点A与AD垂线上找到点D的对应点D′,使点A和点D′之间也是4小格。
4.
顺次连接点A、点B′、点D′、点C′,即可得到旋转后的图形。
C′
B′
D′
一个长方体的底面周长是28cm,高是4cm。这个长方体的棱长总长是多少?
问题
长方体有多少条棱呢?
长方体的对应的棱有什么关系呢?
底面周长等于什么?
长方体有12条棱,相对的棱的长度相等。
相交于同一顶点的三条棱的长度分别是长方体的长、宽、高。
解答:
28×2+4×4=56+16=72(cm)
答:这个长方体的棱长总长是72cm。
底面周长=(长+宽)×2。
三、巩固深化
1.下列运动属于什么现象,填一填。
①电梯的上、下,属于( )现象。
②车轮的转动,属于( )现象。
③观光缆车的移动,属于( )现象。
④直升机螺旋桨的转动,属于( )现象。
平移
旋转
平移
旋转
2.有一个长方体,底面是一个正方形,高18cm,侧面展开正好是一个正方形。这个长方体的体积是( ) cm?。
18cm
18cm
18cm
364.5
18÷4=4.5(cm)
4.5×4.5×18
=20.25×18
=364.5(cm?)
先根据题意画图。
3.分别求出下面长方体、正方体的表面积和体积
(单位:cm)
7.5×4×4+42×2=152(cm2)
4×4×7.5=120(cm3)
1.52×6=13.5(cm2)
1.53=3.375(cm3)
四、课堂小结
观察物体
1.
2.
3.
旋转的特征和性质
长方体、正方体的特征和性质
五、课后作业
1.课本P120,第13、14题;
2.完成练习册本课时的习题。
