中考数学二轮专题复习——多解探究题专题讲义(PDF版,附答案)
文档属性
| 名称 | 中考数学二轮专题复习——多解探究题专题讲义(PDF版,附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 456.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-05 00:00:00 | ||
图片预览




文档简介
二轮复习:多解探究题型
多解探究题,顾名思义是开放型试题的别称,就是说得到的解有多个,一
般情况下,会出现两个解,由于此题型的解不唯一,对学生的能力要求较高。
此类试题对开发学生思维,提高学生数学素养有很大作用,也是中考试题出题
的热点之一。
开放性探究题,分为规律探究、条件探究、结论探究和存在性探究,本节
重点研究条件探究、结论探究和存在性探究试题。
开放性探究题,解题关键在与画出正确形图和满足条件的全部图形。此题
型要注意出现的关键字,如:看到三角形,要分钝角三角形、直角三角形和锐
角三角形讨论;看到直线时,要分在图形内和图形外讨论;看到以一边为边画
等腰三角形的,要分以这条边为腰和底边讨论;看到以一边为边画直角三角形
的,要分以这条边为直角边和斜边讨论等等。
题型一:条件探索型
1、如图,在△ABC 中,AB≠AC,D、E 分别为边 AB、AC 上的点,AC=3AD,AB=3AE,
点 F 为 BC 边上一点,添加一个条件: ,可以使得△FDB 与△ADE 相
似.(只需写出一个)
分析:本题中已给出图形,由于没有给出对应角,所以要分类讨论:对应角或旋转后的角。
2、已知二次函数 y = x2 ? 2mx(m为常数) ,当 ? 1≤ x≤ 2 时,函数值 y 的
最小值为 ? 2 ,则 m 的值是________.
分析:将二次函数化为顶点式,然后分①若 m2,③若?1? m? 2 三种
情况,根据 y 的最小值为-2,结合二次函数的性质即可求解。
题型二:结论探索型
1、在平行四边形 ABCD 中,∠A=30°,AD=4 3,BD=4,则平行四边形 ABCD 的面积
等于 .
分析:本题解题的关键在于画出高线在平行四边形内还是在平行四边形外两种。对图
形进行分类是解决本题的关键,过 D作 DE⊥AB于 E,
解:在 Rt△ADE中,∵∠A=30°,AD=4 ,
∴DE= AD=2 ,AE= AD=6,
在 Rt△BDE中,∵BD=4,
∴BE= = =2,
如图 1,∴AB=8,
∴平行四边形 ABCD的面积=AB?DE=8×2 =16 ,
如图 2,AB=4,
∴平行四边形 ABCD的面积=AB?DE=4×2 =8 ,
2、在矩形纸片 ABCD 中,AD=8,AB=6,E 是边 BC 上的点,将纸片沿 AE 折叠,使点 B 落在
点 F 处,连接 FC,当△EFC 为直角三角形时,BE 的长为 .
分析:应画出如下图的情况:
题型三:存在性探究
1、如图,一次函数 1y k x b? ? ( 1 0k ? )与反比例函数 2
ky
x
? ( 2 0k ? )的图象交于点
( 1, 2)A ? , ( , 1)B m ? .
(1)求这两个函数的表达式;
(2)在 x轴上是否存在点 ( ,0)P n ( 0)n ? ,使 ABP? 为等腰三角形?若存在,求 n的值;
若不存在,说明理由.
中考数学在线:
基础题型:
1、在等腰△ABC中,AB=AC,AB的垂直平分线 DE与 AC所在的直线相交于
所成的锐角是 40°,则∠B=
2、已知三角形相邻两边长分别为 20cm和 30cm,第三边上的高为 10cm,此三
角形的面积为 .
3、已知三角形相邻两边长分别为 20cm和 13cm.第三边上的高为 12cm,则第
三边长为
4、在△ABC中,AB=AC,AB的垂直平分线 DE与 AC所在的直线相交于点 E,
垂足为 D,连接 BE,已知 AE=5, = ,则 BE+CE= .
5、在△ABC中,BC=10,AB的垂直平分线与 AC的垂直平分线分别交 BC于
点 D、E,且 DE=4,则 AD+AE为 .
6、已知:正方形ABCD的边长为 2,点 P是直线CD上一点,若DP=1,则 tan∠BPC
的值是 .
7、已知△ABC中,∠C=90°,BC=2,AC=4,以 AB为边向外作等腰 Rt△ABD,
则 CD=
8、在 Rt△ABC中,∠BAC=90°,AB=AC=1,以 AC为腰作等腰直角三角形 ACD,
则线段 BD的长为 .
能力提升题目:
1、在△ABC中,若∠B=45°,AB=10 2,AC=5 �,则△ABC的面积是______.
2、在? ABCD中,AB<BC,已知∠B=30°,AB=2 ,将△ABC沿 AC翻折至
△AB′C,使点 B′落在? ABCD所在的平面内,连接 B′D.若△AB′D是直角三
角形,则 BC的长为 .
3、在平面直角坐标系中,点 P 的坐标为(0,﹣5),以 P 为圆心的圆与 x 轴相
切,⊙P 的弦 AB(B 点在 A 点右侧)垂直于 y 轴,且 AB=8,反比例函数
ky
x
? (k
≠0)经过点 B,则 k= .
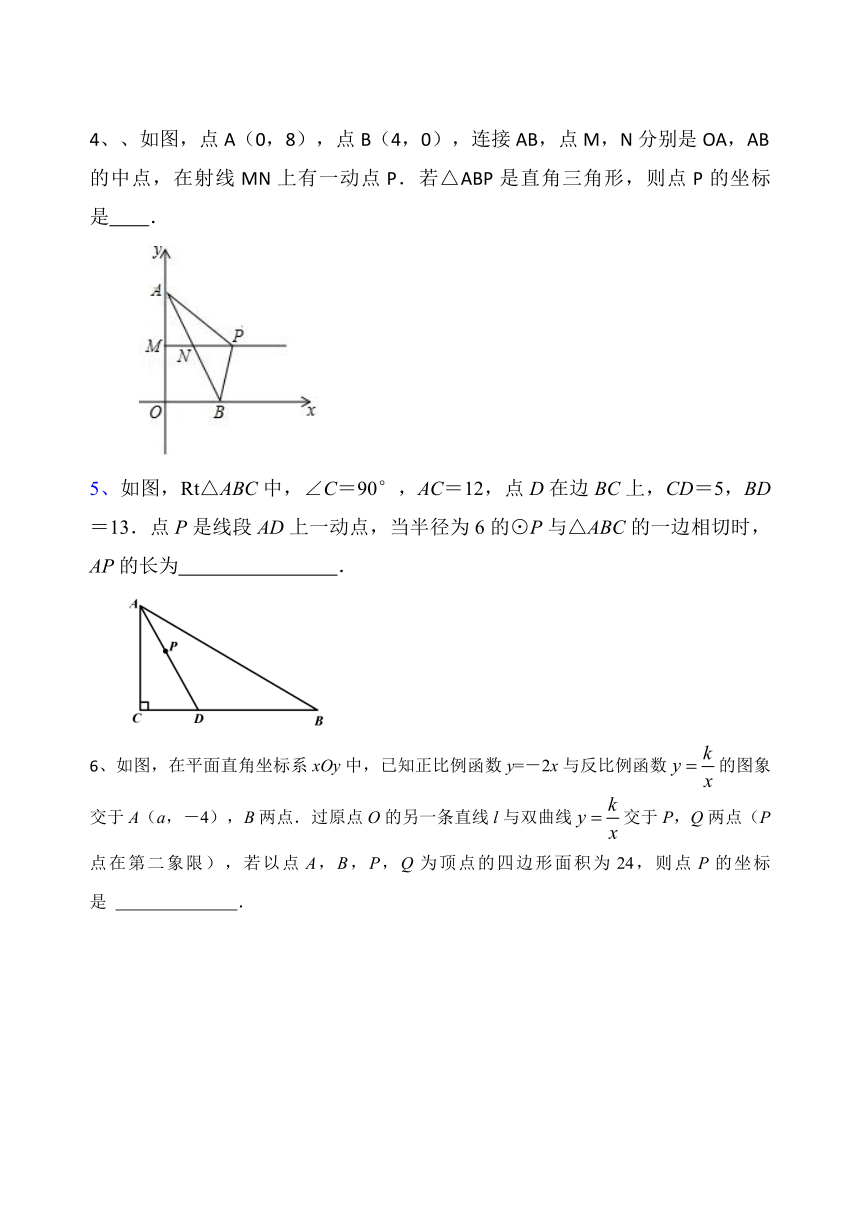
4、、如图,点 A(0,8),点 B(4,0),连接 AB,点 M,N分别是 OA,AB
的中点,在射线 MN 上有一动点 P.若△ABP 是直角三角形,则点 P 的坐标
是 .
5、如图,Rt△ABC中,∠C=90°,AC=12,点 D在边 BC上,CD=5,BD
=13.点 P是线段 AD上一动点,当半径为 6的⊙P与△ABC的一边相切时,
AP的长为 .
6、如图,在平面直角坐标系 xOy中,已知正比例函数 y=-2x与反比例函数
ky
x
? 的图象
交于 A(a,-4),B两点.过原点 O的另一条直线 l与双曲线
ky
x
? 交于 P,Q两点(P
点在第二象限),若以点 A,B,P,Q 为顶点的四边形面积为 24,则点 P 的坐标
是 .
参考答案:
题型一:条件探索型
1、DF∥AC或∠BFD=∠A
2、解 :y=x2?2mx=(x?m)2?m2 ,
①若 m解得:m=?�
2
;
②若 m>2,当 x=2时,y=4?4m=?2,
解得:m=�
2
<2(舍);
③若?1? m? 2,当 x=m 时,y=?m2=?2,
解得:m= 2或 m=? 2∴m的值为?�
2
或 2 ,
题型二:结论探索型 1、故答案为:16 或 8 . 2、3或 6
题型三:存在性探究
1、y=-x+1
172141- ??
中考数学在线:
基础题型:
1、解:如图①:∵DE是 AB的垂直平分线,
∴∠DEA=90°,
∵∠ADE=40°,
∴∠DAE=50°,
∵AB=AC,∠A=∠DAE=50°,
∴∠ABC=∠C= (180°﹣∠A)=65°;
如图②:∵DE是 AB的垂直平分线,
∴∠DEA=90°,
∵∠ADE=40°,
∴∠DAE=50°,
∴∠BAC=130°,
∵AB=AC,
∴∠ABC=∠C= (180°﹣∠A)=25°;
2、解:如图①,在 Rt△ABD中,AB=30,AD=10,
根据勾股定理得:BD= = = =20 ,
在 Rt△ACD中,AC=20,AD=10,
根据勾股定理得:CD= = = =10 ,
∴BC=20 +10 ,
∴S△ABC= BC?AD= (20 +10 )×10=100 +50 ;
如图②,同理可得 BC=20 ﹣10 ,
∴S△ABC= BC?AD= (20 ﹣10 )×10=100 ﹣50 .
3、解:①第三边上的高在三角形内部;
如图 1所示,AB=20cm,AC=13cm,AD=12cm,
∵AD是高,
∴△ABD、△ACD是直角三角形,
∴BD= = =16cm,
同理 CD= =5cm,
∴BC=BD+CD=16+5=21cm;
②第三边上的高在三角形外部;
如图 2所示,AB=20cm,AC=13cm,AD=12cm,
∵AD是高,
∴△ABD、△ACD是直角三角形,
∴BD= = =16cm,
同理可求 CD=5cm,
∴BC=BD﹣CD=16﹣5=11cm.
故选 D.
4、解:①若∠BAC为锐角,如答图 1所示:
∵AB的垂直平分线是 DE,
∴AE=BE,ED⊥AB,AD= AB,
∵AE=5, = ,
∴sin∠AED= ,
∴AD=AE?sin∠AED=3,
∴AB=6,
∴BE+CE=AE+CE=AC=AB=6;
②若∠BAC为钝角,如答图 2所示:
同理可求得:BE+CE=16.
故答案为:6或 16.
5、解:∵AB、AC的垂直平分线分别交 BC于点 D、E,
∴AD=BD,AE=CE,
∴AD+AE=BD+CE,
∵BC=10,DE=4,
∴如图 1,AD+AE=BD+CE=BC﹣DE=10﹣4=6,
如图 2,AD+AE=BD+CE=BC+DE=10+4=14,
综上所述,AD+AE=6 或 14.
故答案为:6或 14.
6、解:此题有两种可能:
(1)∵BC=2,DP=1,
∠C=90°,
∴tan∠BPC= =2;
(2)∵DP=1,DC=2,
∴PC=3,
又∵BC=2,∠C=90°,
∴tan∠BPC= = .
故答案为:2或 .
7、2 或 3 或 .
8、解:①以 A为直角顶点,向外作等腰直角三角形 DAC,
∵∠DAC=90°,且 AD=AC,
∴BD=BA+AD=1+1=2;
②以 C为直角顶点,向外作等腰直角三角形 ACD,
连接 BD,过点 D作 DE⊥BC,交 BC的延长线于 E.
∵△ABC是等腰直角三角形,∠ACD=90°,
∴∠DCE=45°,
又∵DE⊥CE,
∴∠DEC=90°,
∴∠CDE=45°,
∴CE=DE=1× = ;
在 Rt△BAC中,BC= ,
∴BD= ,
③如 3图
此时 BD=1
综上所述:BD的长等于 1或 2或 .
能力提升题目:
1、 75或 25
2、解:当∠B′AD=90°AB<BC时,如图 1,
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,∠B′AD=90°,
∴∠B′GC=90°,
∵∠B=30°,AB=2 ,
∴∠AB′C=30°,
∴GC= B′C= BC,
∴G是 BC的中点,
在 RT△ABG 中,BG= AB= ×2 =3,
∴BC=6;
当∠AB′D=90°时,如图 2,
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形 ACDB′是等腰梯形,
∵∠AB′D=90°,
∴四边形 ACDB′是矩形,
∴∠BAC=90°,
∵∠B=30°,AB=2 ,
∴BC=AB÷ =2 × =4,
∴当 BC的长为 4或 6时,△AB′D是直角三角形.
故答案为:4或 6.
3、﹣8 或﹣32.
4、(2 +2,4)或(2 +2,4).
5、
13
2
或3 13
6、如图所示,当点 P在点 B下方时,过点 P作 PC⊥x轴,BD⊥x轴,
把 A(a,-4) 代入 y=-2x,得 a=2,
∴A(2,-4),点 B的坐标为(-2,4).
∴k=2×(-4)= -8,
∴反比例函数表达式为
8y
x
? ? .
∵S 四边形 PCOB=S 梯形CPBD+S△BOD= S△BOP+ S△POC,S△POC= S△BOD,
∴S 梯形CPBD= S△BOP.
∵点 A、B、P、Q都在反比例函数的图 象上,
∴OA=OB,OP=OQ.
∴四边形 APBQ为平行四边形.
∴S△BOP=
1 24=6
4
? .
设 P(m,
8
m
? )
S 梯形CPBD=
1 8( 4 ( 2 ) 6
2
m
m
? ? ? ? ? ? ?) .
解得:m1=-4,m2=1(舍去)
所以点 P坐标为(-4,2),
同理可得,当点 P在点 B上方时,如图所示:
此时,点 P的坐标为(-1,8).
所以点 P的坐标为(-4,2)或(-1,8).
因此本题答案为(-4,2)或(-1,8).
多解探究题,顾名思义是开放型试题的别称,就是说得到的解有多个,一
般情况下,会出现两个解,由于此题型的解不唯一,对学生的能力要求较高。
此类试题对开发学生思维,提高学生数学素养有很大作用,也是中考试题出题
的热点之一。
开放性探究题,分为规律探究、条件探究、结论探究和存在性探究,本节
重点研究条件探究、结论探究和存在性探究试题。
开放性探究题,解题关键在与画出正确形图和满足条件的全部图形。此题
型要注意出现的关键字,如:看到三角形,要分钝角三角形、直角三角形和锐
角三角形讨论;看到直线时,要分在图形内和图形外讨论;看到以一边为边画
等腰三角形的,要分以这条边为腰和底边讨论;看到以一边为边画直角三角形
的,要分以这条边为直角边和斜边讨论等等。
题型一:条件探索型
1、如图,在△ABC 中,AB≠AC,D、E 分别为边 AB、AC 上的点,AC=3AD,AB=3AE,
点 F 为 BC 边上一点,添加一个条件: ,可以使得△FDB 与△ADE 相
似.(只需写出一个)
分析:本题中已给出图形,由于没有给出对应角,所以要分类讨论:对应角或旋转后的角。
2、已知二次函数 y = x2 ? 2mx(m为常数) ,当 ? 1≤ x≤ 2 时,函数值 y 的
最小值为 ? 2 ,则 m 的值是________.
分析:将二次函数化为顶点式,然后分①若 m2,③若?1? m? 2 三种
情况,根据 y 的最小值为-2,结合二次函数的性质即可求解。
题型二:结论探索型
1、在平行四边形 ABCD 中,∠A=30°,AD=4 3,BD=4,则平行四边形 ABCD 的面积
等于 .
分析:本题解题的关键在于画出高线在平行四边形内还是在平行四边形外两种。对图
形进行分类是解决本题的关键,过 D作 DE⊥AB于 E,
解:在 Rt△ADE中,∵∠A=30°,AD=4 ,
∴DE= AD=2 ,AE= AD=6,
在 Rt△BDE中,∵BD=4,
∴BE= = =2,
如图 1,∴AB=8,
∴平行四边形 ABCD的面积=AB?DE=8×2 =16 ,
如图 2,AB=4,
∴平行四边形 ABCD的面积=AB?DE=4×2 =8 ,
2、在矩形纸片 ABCD 中,AD=8,AB=6,E 是边 BC 上的点,将纸片沿 AE 折叠,使点 B 落在
点 F 处,连接 FC,当△EFC 为直角三角形时,BE 的长为 .
分析:应画出如下图的情况:
题型三:存在性探究
1、如图,一次函数 1y k x b? ? ( 1 0k ? )与反比例函数 2
ky
x
? ( 2 0k ? )的图象交于点
( 1, 2)A ? , ( , 1)B m ? .
(1)求这两个函数的表达式;
(2)在 x轴上是否存在点 ( ,0)P n ( 0)n ? ,使 ABP? 为等腰三角形?若存在,求 n的值;
若不存在,说明理由.
中考数学在线:
基础题型:
1、在等腰△ABC中,AB=AC,AB的垂直平分线 DE与 AC所在的直线相交于
所成的锐角是 40°,则∠B=
2、已知三角形相邻两边长分别为 20cm和 30cm,第三边上的高为 10cm,此三
角形的面积为 .
3、已知三角形相邻两边长分别为 20cm和 13cm.第三边上的高为 12cm,则第
三边长为
4、在△ABC中,AB=AC,AB的垂直平分线 DE与 AC所在的直线相交于点 E,
垂足为 D,连接 BE,已知 AE=5, = ,则 BE+CE= .
5、在△ABC中,BC=10,AB的垂直平分线与 AC的垂直平分线分别交 BC于
点 D、E,且 DE=4,则 AD+AE为 .
6、已知:正方形ABCD的边长为 2,点 P是直线CD上一点,若DP=1,则 tan∠BPC
的值是 .
7、已知△ABC中,∠C=90°,BC=2,AC=4,以 AB为边向外作等腰 Rt△ABD,
则 CD=
8、在 Rt△ABC中,∠BAC=90°,AB=AC=1,以 AC为腰作等腰直角三角形 ACD,
则线段 BD的长为 .
能力提升题目:
1、在△ABC中,若∠B=45°,AB=10 2,AC=5 �,则△ABC的面积是______.
2、在? ABCD中,AB<BC,已知∠B=30°,AB=2 ,将△ABC沿 AC翻折至
△AB′C,使点 B′落在? ABCD所在的平面内,连接 B′D.若△AB′D是直角三
角形,则 BC的长为 .
3、在平面直角坐标系中,点 P 的坐标为(0,﹣5),以 P 为圆心的圆与 x 轴相
切,⊙P 的弦 AB(B 点在 A 点右侧)垂直于 y 轴,且 AB=8,反比例函数
ky
x
? (k
≠0)经过点 B,则 k= .
4、、如图,点 A(0,8),点 B(4,0),连接 AB,点 M,N分别是 OA,AB
的中点,在射线 MN 上有一动点 P.若△ABP 是直角三角形,则点 P 的坐标
是 .
5、如图,Rt△ABC中,∠C=90°,AC=12,点 D在边 BC上,CD=5,BD
=13.点 P是线段 AD上一动点,当半径为 6的⊙P与△ABC的一边相切时,
AP的长为 .
6、如图,在平面直角坐标系 xOy中,已知正比例函数 y=-2x与反比例函数
ky
x
? 的图象
交于 A(a,-4),B两点.过原点 O的另一条直线 l与双曲线
ky
x
? 交于 P,Q两点(P
点在第二象限),若以点 A,B,P,Q 为顶点的四边形面积为 24,则点 P 的坐标
是 .
参考答案:
题型一:条件探索型
1、DF∥AC或∠BFD=∠A
2、解 :y=x2?2mx=(x?m)2?m2 ,
①若 m解得:m=?�
2
;
②若 m>2,当 x=2时,y=4?4m=?2,
解得:m=�
2
<2(舍);
③若?1? m? 2,当 x=m 时,y=?m2=?2,
解得:m= 2或 m=? 2∴m的值为?�
2
或 2 ,
题型二:结论探索型 1、故答案为:16 或 8 . 2、3或 6
题型三:存在性探究
1、y=-x+1
172141- ??
中考数学在线:
基础题型:
1、解:如图①:∵DE是 AB的垂直平分线,
∴∠DEA=90°,
∵∠ADE=40°,
∴∠DAE=50°,
∵AB=AC,∠A=∠DAE=50°,
∴∠ABC=∠C= (180°﹣∠A)=65°;
如图②:∵DE是 AB的垂直平分线,
∴∠DEA=90°,
∵∠ADE=40°,
∴∠DAE=50°,
∴∠BAC=130°,
∵AB=AC,
∴∠ABC=∠C= (180°﹣∠A)=25°;
2、解:如图①,在 Rt△ABD中,AB=30,AD=10,
根据勾股定理得:BD= = = =20 ,
在 Rt△ACD中,AC=20,AD=10,
根据勾股定理得:CD= = = =10 ,
∴BC=20 +10 ,
∴S△ABC= BC?AD= (20 +10 )×10=100 +50 ;
如图②,同理可得 BC=20 ﹣10 ,
∴S△ABC= BC?AD= (20 ﹣10 )×10=100 ﹣50 .
3、解:①第三边上的高在三角形内部;
如图 1所示,AB=20cm,AC=13cm,AD=12cm,
∵AD是高,
∴△ABD、△ACD是直角三角形,
∴BD= = =16cm,
同理 CD= =5cm,
∴BC=BD+CD=16+5=21cm;
②第三边上的高在三角形外部;
如图 2所示,AB=20cm,AC=13cm,AD=12cm,
∵AD是高,
∴△ABD、△ACD是直角三角形,
∴BD= = =16cm,
同理可求 CD=5cm,
∴BC=BD﹣CD=16﹣5=11cm.
故选 D.
4、解:①若∠BAC为锐角,如答图 1所示:
∵AB的垂直平分线是 DE,
∴AE=BE,ED⊥AB,AD= AB,
∵AE=5, = ,
∴sin∠AED= ,
∴AD=AE?sin∠AED=3,
∴AB=6,
∴BE+CE=AE+CE=AC=AB=6;
②若∠BAC为钝角,如答图 2所示:
同理可求得:BE+CE=16.
故答案为:6或 16.
5、解:∵AB、AC的垂直平分线分别交 BC于点 D、E,
∴AD=BD,AE=CE,
∴AD+AE=BD+CE,
∵BC=10,DE=4,
∴如图 1,AD+AE=BD+CE=BC﹣DE=10﹣4=6,
如图 2,AD+AE=BD+CE=BC+DE=10+4=14,
综上所述,AD+AE=6 或 14.
故答案为:6或 14.
6、解:此题有两种可能:
(1)∵BC=2,DP=1,
∠C=90°,
∴tan∠BPC= =2;
(2)∵DP=1,DC=2,
∴PC=3,
又∵BC=2,∠C=90°,
∴tan∠BPC= = .
故答案为:2或 .
7、2 或 3 或 .
8、解:①以 A为直角顶点,向外作等腰直角三角形 DAC,
∵∠DAC=90°,且 AD=AC,
∴BD=BA+AD=1+1=2;
②以 C为直角顶点,向外作等腰直角三角形 ACD,
连接 BD,过点 D作 DE⊥BC,交 BC的延长线于 E.
∵△ABC是等腰直角三角形,∠ACD=90°,
∴∠DCE=45°,
又∵DE⊥CE,
∴∠DEC=90°,
∴∠CDE=45°,
∴CE=DE=1× = ;
在 Rt△BAC中,BC= ,
∴BD= ,
③如 3图
此时 BD=1
综上所述:BD的长等于 1或 2或 .
能力提升题目:
1、 75或 25
2、解:当∠B′AD=90°AB<BC时,如图 1,
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,∠B′AD=90°,
∴∠B′GC=90°,
∵∠B=30°,AB=2 ,
∴∠AB′C=30°,
∴GC= B′C= BC,
∴G是 BC的中点,
在 RT△ABG 中,BG= AB= ×2 =3,
∴BC=6;
当∠AB′D=90°时,如图 2,
∵AD=BC,BC=B′C,
∴AD=B′C,
∵AC∥B′D,
∴四边形 ACDB′是等腰梯形,
∵∠AB′D=90°,
∴四边形 ACDB′是矩形,
∴∠BAC=90°,
∵∠B=30°,AB=2 ,
∴BC=AB÷ =2 × =4,
∴当 BC的长为 4或 6时,△AB′D是直角三角形.
故答案为:4或 6.
3、﹣8 或﹣32.
4、(2 +2,4)或(2 +2,4).
5、
13
2
或3 13
6、如图所示,当点 P在点 B下方时,过点 P作 PC⊥x轴,BD⊥x轴,
把 A(a,-4) 代入 y=-2x,得 a=2,
∴A(2,-4),点 B的坐标为(-2,4).
∴k=2×(-4)= -8,
∴反比例函数表达式为
8y
x
? ? .
∵S 四边形 PCOB=S 梯形CPBD+S△BOD= S△BOP+ S△POC,S△POC= S△BOD,
∴S 梯形CPBD= S△BOP.
∵点 A、B、P、Q都在反比例函数的图 象上,
∴OA=OB,OP=OQ.
∴四边形 APBQ为平行四边形.
∴S△BOP=
1 24=6
4
? .
设 P(m,
8
m
? )
S 梯形CPBD=
1 8( 4 ( 2 ) 6
2
m
m
? ? ? ? ? ? ?) .
解得:m1=-4,m2=1(舍去)
所以点 P坐标为(-4,2),
同理可得,当点 P在点 B上方时,如图所示:
此时,点 P的坐标为(-1,8).
所以点 P的坐标为(-4,2)或(-1,8).
因此本题答案为(-4,2)或(-1,8).
同课章节目录
