人教版五上数学整理与复习:多边形面积教学课件(共43张ppt)
文档属性
| 名称 | 人教版五上数学整理与复习:多边形面积教学课件(共43张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-05 19:48:50 | ||
图片预览




文档简介
(共43张PPT)
多边形面积
图形与几何(一)
RJ 五年级上册
这个图形可以分成一个( )形和一个( )形,其中( )形的面积是( )m2,( )形的面积是( )m2,所以这个图形的面积是( )m2。
长方
三角
长方
50
三角
10
60
(1)掌握平行四边形、三角形、梯形的面积计算公式及公式之间的关系,会计算组合图形的面积。
(2)体验图形的平移、旋转以及转化的数学思想方法。
课后作业
知识梳理
深化知识
拓展延伸
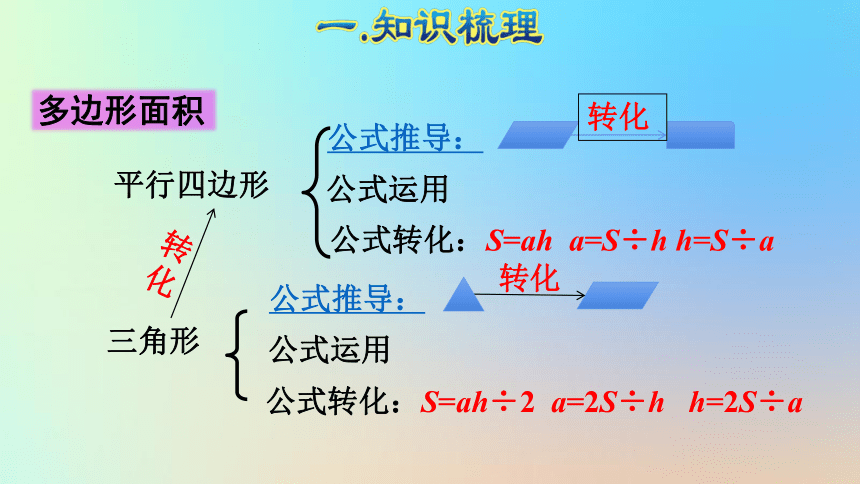
公式推导:
公式运用
公式转化:S=ah a=S÷h h=S÷a
平行四边形
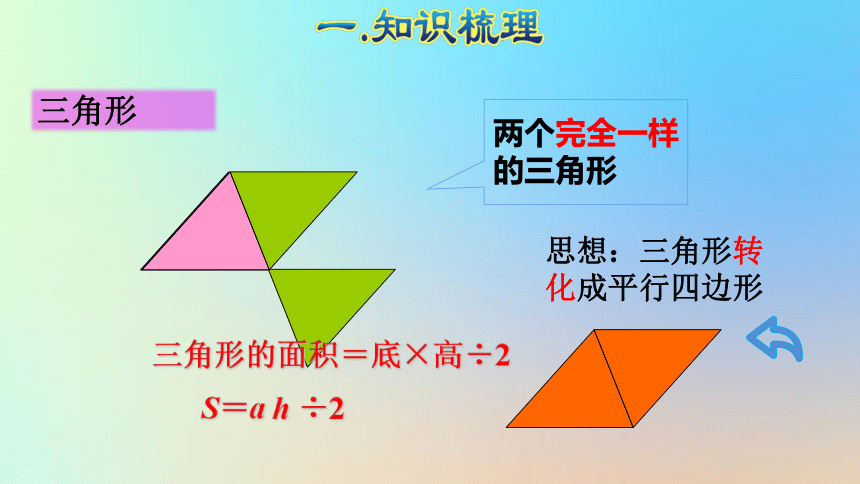
三角形
公式推导:
公式运用
公式转化:S=ah÷2 a=2S÷h h=2S÷a
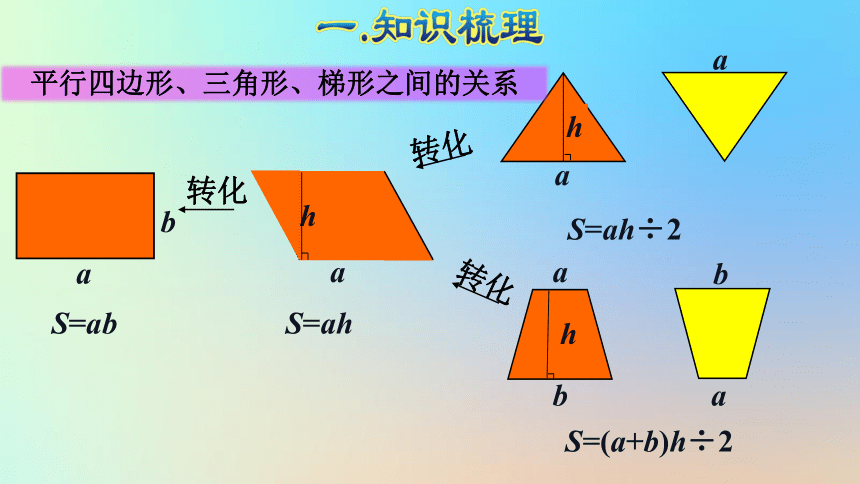
转化
转化
转化
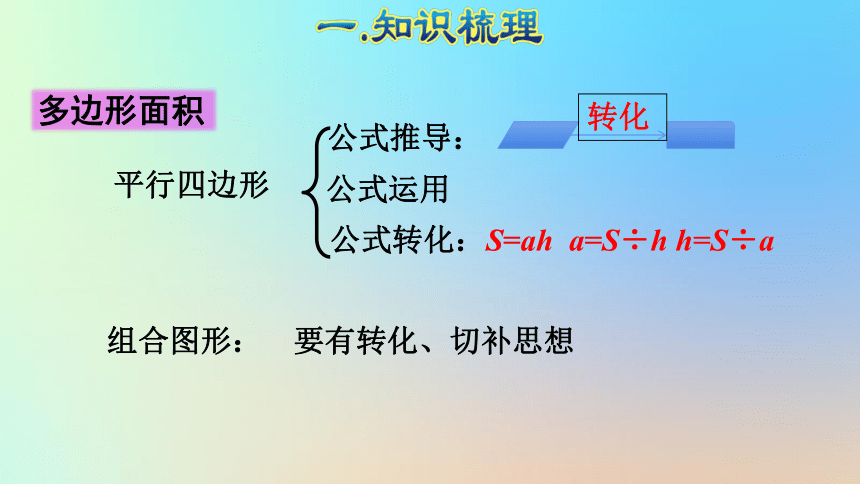
公式推导:
公式运用
公式转化:S=ah a=S÷h h=S÷a
平行四边形
梯形
公式推导:
公式运用
公式转化:S=(a+b)h÷2 h=2S÷(a+b) (a+b)=2S÷h
转化
转化
转化
公式推导:
公式运用
公式转化:S=ah a=S÷h h=S÷a
平行四边形
组合图形:
转化
要有转化、切补思想
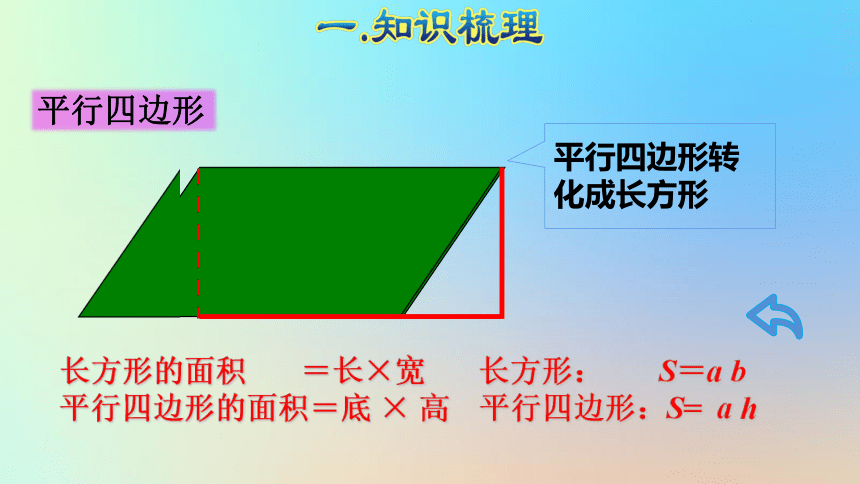
长方形的面积 =长×宽
平行四边形的面积=底 × 高
长方形: S=a b
平行四边形:S= a h
平行四边形转化成长方形
三角形的面积=底×高÷2
S=a h ÷2
思想:三角形转化成平行四边形
两个完全一样的三角形
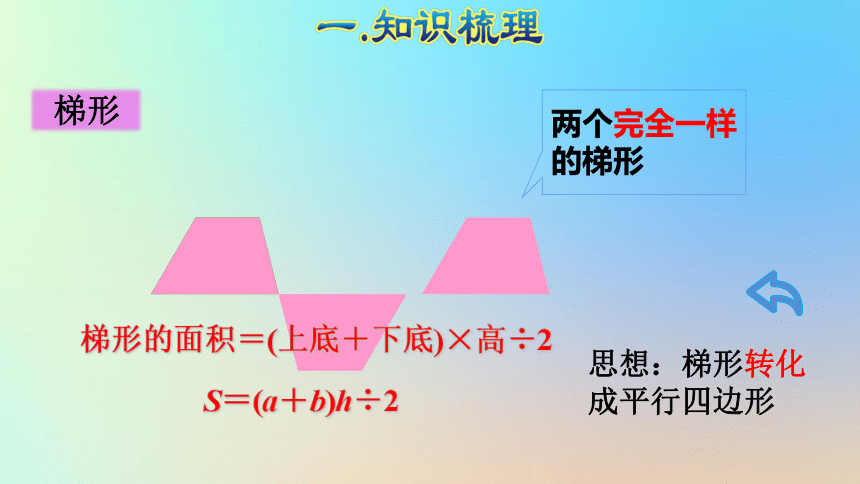
两个完全一样的梯形
S=(a+b)h÷2
思想:梯形转化成平行四边形
梯形的面积=(上底+下底)×高÷2
a
a
b
h
h
S=ah
S=ah÷2
S=(a+b)h÷2
a
S=ab
b
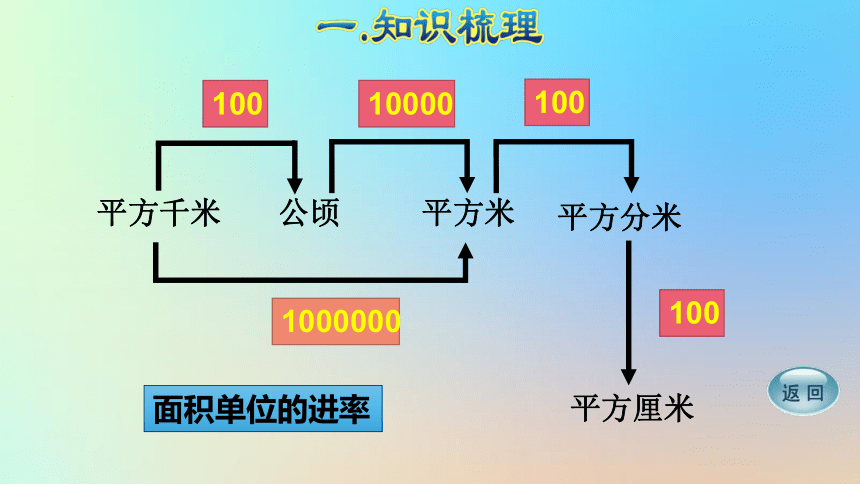
平方千米
公顷
平方米
平方分米
平方厘米
100
10000
100
100
1000000
面积单位的进率
1、公式应用及转化
求面积。
S=ah
S=ah÷2
S=(a+b)h÷2
图形 平行四边形 三角形 梯形
底/ cm 7.5 6 10.2 24 上 4.2 下6.7 上8 下12
高/ cm 3.12 4.3 5.8 12.5 4 15
面积 / cm2
h=S÷a
h=2S÷a
3m
6dm
图形 底 高 面积
平行四边形 4m ① 12㎡
三角形 ② 8dm 24 d㎡
3m
h=2S÷(a+b)
图形 底 高 面积
梯形 上底4cm
下底6cm ③ 25m2
2、面积单位换算
①520公顷=( )平方千米
②0.27平方千米=( )公顷
5.2
27
小化大÷100
大化小×100
③1.8公顷=( )平方千米
④1.5公顷=( )平方米
⑤1.15平方米=( )平方分米=( )平方厘米
0.018
15000
115
11500
小化大÷100
大化小×10000
大化小×100
大化小×100
3、面积的应用
一、我会正确判断。
1.平行四边形的底越长,它的面积就越大。( )
2.面积相等的两个梯形一定能拼成一个平行四边形。 ( )
3.面积相等的两个三角形,形状也一定相同。 ( )
二、我会正确选择。
(1)两个( )的三角形可以拼成一个平行四边形.
A.面积相等 B.形状相同
C.等底等高 D.完全一样
D
(2)一个三角形,面积20平方米,高10米,底是( )米。
A.200 B.2 C.4
(3)下图中甲、乙两部分的面积相比较,( )
A.甲>乙 B.甲<乙 C.甲=乙
S红-?= 甲= S蓝-?= 乙
A
B
C
D
?
C
C
a=2S÷h
分的方法1
长方形加上梯形
长方形的面积=6×5=30(cm2)
梯形的面积=(5+10)×(12-6)÷2
=15×6÷2
=45(cm2)
组合图形的面积=30+45=75(cm2)
4、多边形面积的应用
分的方法2
三角形加上梯形
三角形的面积=10×(12-6)÷2
=10×6÷2
=30(cm2)
梯形的面积=(6+12)×5÷2
=18×5÷2
=45(cm2)
组合图形的面积=30+45=75(cm2)
4m
2m
求阴影部分的面积.
2×2+4×4-4×6÷2
=8+16-12
=12(m2)
1.填空。
(1)一个三角形和一个平行四边形等底等高,三角形的面积是12 m2,平行四边形的面积是( )。
(2)一个三角形和一个平行四边形的面积相等,高也相等。如果三角形的底等于15 cm,那么平行四边形的底是( )cm。
24m2
7.5
1.填空。
(3)若三角形的底缩小2倍,高扩大四倍,那么它的面积( )。
(4)一个平行四边形的底和高分别等于长方形的长和宽,已知长方形的面积是28 cm2,这个平行四边形的面积是( ) dm2。
扩大2倍
0.28
1.填空。
(5)如右图,阴影部分的面积是28 cm2,平行四边形的面积是( )cm2
56
平行四边形的面积=2×三角形的面积=2×28=56(cm 2)
(1)三角形的面积等于平行四边形面积的一半。( )
(2)一个三角形的底扩大2倍,高不变,它的面积也会扩大2倍。 ( )
(3)两个面积相等的梯形,形状也一定相同。( )
2.判断。
2.判断。
(4)把一个长方形的木条框架拉成一个平行四边形,它的周长和面积都不变。 ( )
(5)周长相等的两个平行四边形面积一定相等。( )
(6)等底等高的两个三角形,形状不一定相同,但它们的面积一定相等。 ( )
3. 选择。
(1)两个平行四边形面积相等,它们的底和高( )。
A .一定相等
B. 不一定相等
C. 一定不相等
B
(2)求直角三角形的面积
①3×4÷2 ②3×5÷2
③4×5÷2 ④5×2.4÷2
⑤3×2.4÷2 ⑥4×2.4÷2
哪些算式正确?( )
①④
(3)一个三角形,高不变,底扩大3倍,面积就扩大( )倍。
3 B. 6 C. 9
(4)把一个平行四边形任意分割成两个梯形,这两个梯形的( )总是相等。
A. 上、下底的和 B. 面积 C. 高
A
C
4.选用合适的条件计算下列图形的面积。(单位:m)
7×8÷2=28(m2)
4.选用合适的条件计算下列图形的面积。(单位:m)
2.2×9=19.8(m2)
4.选用合适的条件计算下列图形的面积。(单位:m)
(3+5)×3÷2=12(m2)
5.面积单位我会用
6公顷=( )平方米 700平方千米=( )公顷
80公顷=( )平方米=( )平方千米
一块黑板的面积大约是400( )
校园占地面积大约是2( )
安徽省的面积大约是14万( )
平方厘米
公顷
平方千米
60000
70000
800000
0.8
6.解决问题
(1)一个三角形的底是15厘米,如果底缩小3厘米,面积就缩小18平方厘米。原来三角形的面积是( )平方厘米。
18×2÷3=12(cm)
(15+3)×12÷2=108(cm2)
108
6.解决问题
(2)一堆钢管,最高层12根,最下层23根,从上到下每层(最上层除外)比上一层多1根,共堆了12层,这样的两堆钢管一共有多少根?
(12+23)×12÷2×2=420(根)
6.解决问题
(3)下图是教室的一面墙。如果砌这面墙每平方米用砖185块,一共需要多少块砖?
这面墙的面积=三角形的面积+长方形的面积
6.解决问题
(3)下图是教室的一面墙。如果砌这面墙每平方米用砖185块,一共需要多少块砖?
185×(5×4+5×1.2÷2)=4255(块)
7.解决问题:张大爷用篱笆围成一个如下图所示的梯形养鸡场,一边靠墙,篱笆长108.6米,这个养鸡场的面积是多少?
7.解决问题:张大爷用篱笆围成一个如下图所示的梯形养鸡场,一边靠墙,篱笆长108.6米,这个养鸡场的面积是多少?
解:因为养鸡场是一个梯形,篱笆的总长是108.6米,那么梯形的上底和下底的和是:
108.6-27.8=80.8(米),
那么梯形的面积是:
80.8×27.8÷2=1 123.12(平方米).
作 业 从课后习题中选取。
多边形面积
图形与几何(一)
RJ 五年级上册
这个图形可以分成一个( )形和一个( )形,其中( )形的面积是( )m2,( )形的面积是( )m2,所以这个图形的面积是( )m2。
长方
三角
长方
50
三角
10
60
(1)掌握平行四边形、三角形、梯形的面积计算公式及公式之间的关系,会计算组合图形的面积。
(2)体验图形的平移、旋转以及转化的数学思想方法。
课后作业
知识梳理
深化知识
拓展延伸
公式推导:
公式运用
公式转化:S=ah a=S÷h h=S÷a
平行四边形
三角形
公式推导:
公式运用
公式转化:S=ah÷2 a=2S÷h h=2S÷a
转化
转化
转化
公式推导:
公式运用
公式转化:S=ah a=S÷h h=S÷a
平行四边形
梯形
公式推导:
公式运用
公式转化:S=(a+b)h÷2 h=2S÷(a+b) (a+b)=2S÷h
转化
转化
转化
公式推导:
公式运用
公式转化:S=ah a=S÷h h=S÷a
平行四边形
组合图形:
转化
要有转化、切补思想
长方形的面积 =长×宽
平行四边形的面积=底 × 高
长方形: S=a b
平行四边形:S= a h
平行四边形转化成长方形
三角形的面积=底×高÷2
S=a h ÷2
思想:三角形转化成平行四边形
两个完全一样的三角形
两个完全一样的梯形
S=(a+b)h÷2
思想:梯形转化成平行四边形
梯形的面积=(上底+下底)×高÷2
a
a
b
h
h
S=ah
S=ah÷2
S=(a+b)h÷2
a
S=ab
b
平方千米
公顷
平方米
平方分米
平方厘米
100
10000
100
100
1000000
面积单位的进率
1、公式应用及转化
求面积。
S=ah
S=ah÷2
S=(a+b)h÷2
图形 平行四边形 三角形 梯形
底/ cm 7.5 6 10.2 24 上 4.2 下6.7 上8 下12
高/ cm 3.12 4.3 5.8 12.5 4 15
面积 / cm2
h=S÷a
h=2S÷a
3m
6dm
图形 底 高 面积
平行四边形 4m ① 12㎡
三角形 ② 8dm 24 d㎡
3m
h=2S÷(a+b)
图形 底 高 面积
梯形 上底4cm
下底6cm ③ 25m2
2、面积单位换算
①520公顷=( )平方千米
②0.27平方千米=( )公顷
5.2
27
小化大÷100
大化小×100
③1.8公顷=( )平方千米
④1.5公顷=( )平方米
⑤1.15平方米=( )平方分米=( )平方厘米
0.018
15000
115
11500
小化大÷100
大化小×10000
大化小×100
大化小×100
3、面积的应用
一、我会正确判断。
1.平行四边形的底越长,它的面积就越大。( )
2.面积相等的两个梯形一定能拼成一个平行四边形。 ( )
3.面积相等的两个三角形,形状也一定相同。 ( )
二、我会正确选择。
(1)两个( )的三角形可以拼成一个平行四边形.
A.面积相等 B.形状相同
C.等底等高 D.完全一样
D
(2)一个三角形,面积20平方米,高10米,底是( )米。
A.200 B.2 C.4
(3)下图中甲、乙两部分的面积相比较,( )
A.甲>乙 B.甲<乙 C.甲=乙
S红-?= 甲= S蓝-?= 乙
A
B
C
D
?
C
C
a=2S÷h
分的方法1
长方形加上梯形
长方形的面积=6×5=30(cm2)
梯形的面积=(5+10)×(12-6)÷2
=15×6÷2
=45(cm2)
组合图形的面积=30+45=75(cm2)
4、多边形面积的应用
分的方法2
三角形加上梯形
三角形的面积=10×(12-6)÷2
=10×6÷2
=30(cm2)
梯形的面积=(6+12)×5÷2
=18×5÷2
=45(cm2)
组合图形的面积=30+45=75(cm2)
4m
2m
求阴影部分的面积.
2×2+4×4-4×6÷2
=8+16-12
=12(m2)
1.填空。
(1)一个三角形和一个平行四边形等底等高,三角形的面积是12 m2,平行四边形的面积是( )。
(2)一个三角形和一个平行四边形的面积相等,高也相等。如果三角形的底等于15 cm,那么平行四边形的底是( )cm。
24m2
7.5
1.填空。
(3)若三角形的底缩小2倍,高扩大四倍,那么它的面积( )。
(4)一个平行四边形的底和高分别等于长方形的长和宽,已知长方形的面积是28 cm2,这个平行四边形的面积是( ) dm2。
扩大2倍
0.28
1.填空。
(5)如右图,阴影部分的面积是28 cm2,平行四边形的面积是( )cm2
56
平行四边形的面积=2×三角形的面积=2×28=56(cm 2)
(1)三角形的面积等于平行四边形面积的一半。( )
(2)一个三角形的底扩大2倍,高不变,它的面积也会扩大2倍。 ( )
(3)两个面积相等的梯形,形状也一定相同。( )
2.判断。
2.判断。
(4)把一个长方形的木条框架拉成一个平行四边形,它的周长和面积都不变。 ( )
(5)周长相等的两个平行四边形面积一定相等。( )
(6)等底等高的两个三角形,形状不一定相同,但它们的面积一定相等。 ( )
3. 选择。
(1)两个平行四边形面积相等,它们的底和高( )。
A .一定相等
B. 不一定相等
C. 一定不相等
B
(2)求直角三角形的面积
①3×4÷2 ②3×5÷2
③4×5÷2 ④5×2.4÷2
⑤3×2.4÷2 ⑥4×2.4÷2
哪些算式正确?( )
①④
(3)一个三角形,高不变,底扩大3倍,面积就扩大( )倍。
3 B. 6 C. 9
(4)把一个平行四边形任意分割成两个梯形,这两个梯形的( )总是相等。
A. 上、下底的和 B. 面积 C. 高
A
C
4.选用合适的条件计算下列图形的面积。(单位:m)
7×8÷2=28(m2)
4.选用合适的条件计算下列图形的面积。(单位:m)
2.2×9=19.8(m2)
4.选用合适的条件计算下列图形的面积。(单位:m)
(3+5)×3÷2=12(m2)
5.面积单位我会用
6公顷=( )平方米 700平方千米=( )公顷
80公顷=( )平方米=( )平方千米
一块黑板的面积大约是400( )
校园占地面积大约是2( )
安徽省的面积大约是14万( )
平方厘米
公顷
平方千米
60000
70000
800000
0.8
6.解决问题
(1)一个三角形的底是15厘米,如果底缩小3厘米,面积就缩小18平方厘米。原来三角形的面积是( )平方厘米。
18×2÷3=12(cm)
(15+3)×12÷2=108(cm2)
108
6.解决问题
(2)一堆钢管,最高层12根,最下层23根,从上到下每层(最上层除外)比上一层多1根,共堆了12层,这样的两堆钢管一共有多少根?
(12+23)×12÷2×2=420(根)
6.解决问题
(3)下图是教室的一面墙。如果砌这面墙每平方米用砖185块,一共需要多少块砖?
这面墙的面积=三角形的面积+长方形的面积
6.解决问题
(3)下图是教室的一面墙。如果砌这面墙每平方米用砖185块,一共需要多少块砖?
185×(5×4+5×1.2÷2)=4255(块)
7.解决问题:张大爷用篱笆围成一个如下图所示的梯形养鸡场,一边靠墙,篱笆长108.6米,这个养鸡场的面积是多少?
7.解决问题:张大爷用篱笆围成一个如下图所示的梯形养鸡场,一边靠墙,篱笆长108.6米,这个养鸡场的面积是多少?
解:因为养鸡场是一个梯形,篱笆的总长是108.6米,那么梯形的上底和下底的和是:
108.6-27.8=80.8(米),
那么梯形的面积是:
80.8×27.8÷2=1 123.12(平方米).
作 业 从课后习题中选取。
