2.4抛物线及其标准方程 第一课时 课件(共18张PPT)
文档属性
| 名称 | 2.4抛物线及其标准方程 第一课时 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-08 11:56:53 | ||
图片预览





文档简介
(共18张PPT)
(第一课时)
二次函数是开口向上或向下的抛物线
一、新知探究
生活中存在各种形式的抛物线
一、新知探究
投篮运动
抛球运动
一、新知探究
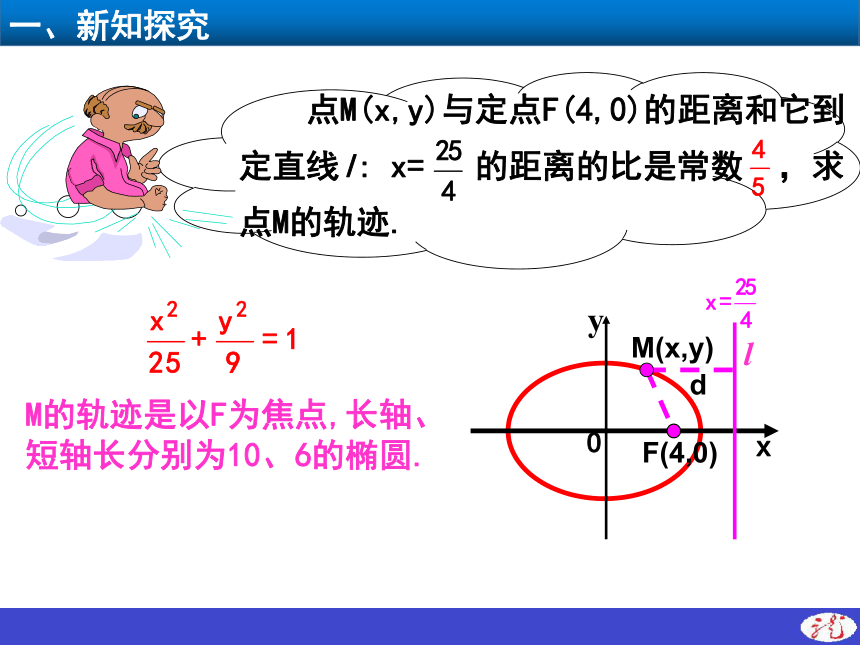
M的轨迹是以F为焦点,长轴、
短轴长分别为10、6的椭圆.
一、新知探究
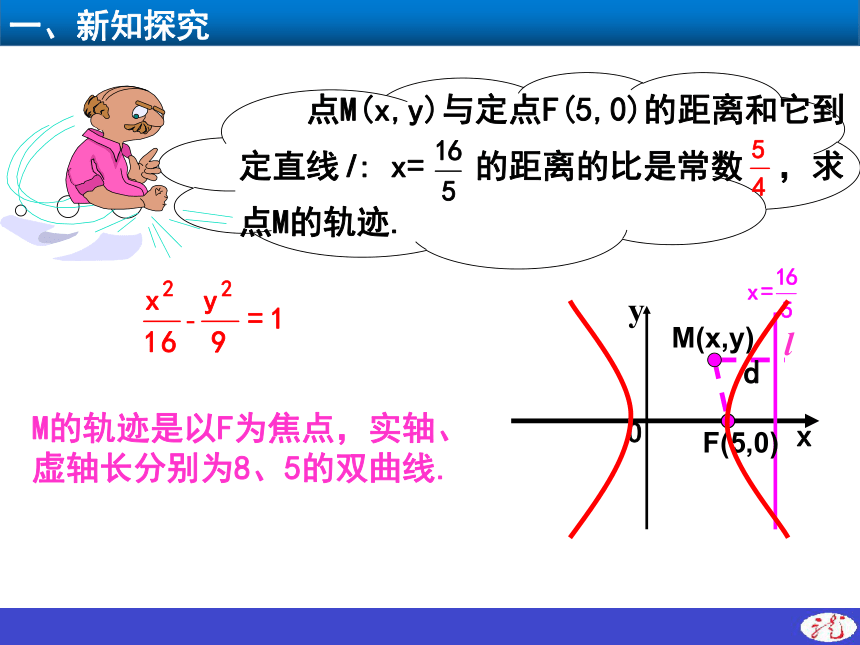
M的轨迹是以F为焦点,实轴、
虚轴长分别为8、5的双曲线.
一、新知探究
一、新知探究
在平面内,到一个定点F距离和定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物线.
点F叫做抛物线的焦点,
直线l 叫抛物线的准线.
准线
焦点
d
F在l上时,轨迹是过点F垂直于l的一条直线.
二、抛物线的定义
x
x
x
y
y
y
o
o
o
三、抛物线的标准方程
K
设︱KF︱= p
设点M的坐标为(x,y),
由定义可知,
取过焦点F且垂直于准线l的直线为x轴,线段KF的中垂线y轴.
三、抛物线的标准方程
方程 y2 = 2px(p>0)叫做抛物线的标准方程.
其中 p 为正常数,它的几何意义是:
焦点到准线的距离
它表示抛物线的焦点在 X轴的
正半轴上.
三、抛物线的标准方程
三、抛物线的标准方程
图形 标准方程 焦点坐标 准线方程
1.一次项的变量为抛物线的焦点所在轴,且一次项系数为正就在正半轴,一次项系数为负就在负半轴.
2.一次项系数的正负决定了抛物线的开口方向.
三、抛物线的标准方程
例1 求适合下列条件的抛物线的标准方程:
(1)焦点是F(0,-2) (2)准线为y=-1
(3)过点M(-6,6) (4)焦点在直线l:3x-2y-6=0上
解:
四、精典例题
解:
例2 (1)如果抛物线的顶点在原点,焦点在y轴上,抛物线上
一点M(m,-3)到焦点的距离等于5,求抛物线方程.
(2)点M与点F(2,0)的距离比它到直线x=-4的距离
小2,求M的轨迹方程.
.
M(m,-3)
F
N
x
y
x
y
x=-4
x=-2
F
O
M
A
N
四、精典例题
在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.
y2=-2px
(p>0)
x2=2py
(p>0)
y2=2px
(p>0)
x2=-2py
(p>0)
五、课堂小结
定义 图形 标准方程 焦点 准线方程
第73页习题2.4A组第3、4题
课堂作业
第67页练习第1题
第73页习题2.4A组第2题
课堂练习
六、巩固提升
(第一课时)
二次函数是开口向上或向下的抛物线
一、新知探究
生活中存在各种形式的抛物线
一、新知探究
投篮运动
抛球运动
一、新知探究
M的轨迹是以F为焦点,长轴、
短轴长分别为10、6的椭圆.
一、新知探究
M的轨迹是以F为焦点,实轴、
虚轴长分别为8、5的双曲线.
一、新知探究
一、新知探究
在平面内,到一个定点F距离和定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物线.
点F叫做抛物线的焦点,
直线l 叫抛物线的准线.
准线
焦点
d
F在l上时,轨迹是过点F垂直于l的一条直线.
二、抛物线的定义
x
x
x
y
y
y
o
o
o
三、抛物线的标准方程
K
设︱KF︱= p
设点M的坐标为(x,y),
由定义可知,
取过焦点F且垂直于准线l的直线为x轴,线段KF的中垂线y轴.
三、抛物线的标准方程
方程 y2 = 2px(p>0)叫做抛物线的标准方程.
其中 p 为正常数,它的几何意义是:
焦点到准线的距离
它表示抛物线的焦点在 X轴的
正半轴上.
三、抛物线的标准方程
三、抛物线的标准方程
图形 标准方程 焦点坐标 准线方程
1.一次项的变量为抛物线的焦点所在轴,且一次项系数为正就在正半轴,一次项系数为负就在负半轴.
2.一次项系数的正负决定了抛物线的开口方向.
三、抛物线的标准方程
例1 求适合下列条件的抛物线的标准方程:
(1)焦点是F(0,-2) (2)准线为y=-1
(3)过点M(-6,6) (4)焦点在直线l:3x-2y-6=0上
解:
四、精典例题
解:
例2 (1)如果抛物线的顶点在原点,焦点在y轴上,抛物线上
一点M(m,-3)到焦点的距离等于5,求抛物线方程.
(2)点M与点F(2,0)的距离比它到直线x=-4的距离
小2,求M的轨迹方程.
.
M(m,-3)
F
N
x
y
x
y
x=-4
x=-2
F
O
M
A
N
四、精典例题
在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.
y2=-2px
(p>0)
x2=2py
(p>0)
y2=2px
(p>0)
x2=-2py
(p>0)
五、课堂小结
定义 图形 标准方程 焦点 准线方程
第73页习题2.4A组第3、4题
课堂作业
第67页练习第1题
第73页习题2.4A组第2题
课堂练习
六、巩固提升
