苏科版八年级下册10.1 分式 课件(20张)
文档属性
| 名称 | 苏科版八年级下册10.1 分式 课件(20张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-06 09:52:02 | ||
图片预览








文档简介
(共20张PPT)
分式
创设情境
2.一块长方形玻璃的面积为2 m2,
如果长是3 m,那么宽是 m;
2 m2
如果宽是a m,那么长是 m.
1.如果某市人口总数为a人,绿地面积为b m2,那么该市
人均拥有绿地 m2.
创设情境
3.如果面积为a公顷、 b公顷的两块棉田分别产棉花m 千克、
n千克,那么这两块棉田平均每公顷产棉花 千克.
4.已知A、B两地的路程为s km,甲乙两人分别从A、B两
地同时出发相向而行,甲的速度是x km/h,乙的速度是
y km/h,那么经过______h两人相遇.
创设情境
5.小明用a元钱去购买练习本,原价每本b元,如果每本降
价1元,那么现在可以购买练习本 本.
这些代数式有什么共同的特征?
探索活动
形如 (A、B是整式,且B中含有字母,B≠0) 的式子,
叫做分式.
其中A叫做分式的分子,B叫做分式的分母.
A
B
探索活动
分式与整式有什么不同?
整式和分式统称有理式,即:
有理式
整式
分式
分母不含字母
分母含字母
分母含字母
单项式和多项式(分母中不含字母)
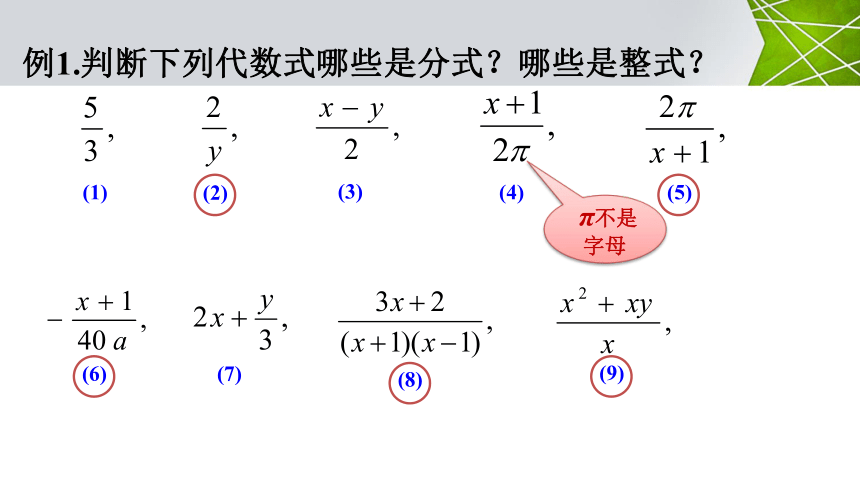
例1.判断下列代数式哪些是分式?哪些是整式?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
π不是字母
分式可以表示现实生活中的一些数量关系:
1.如果某市人口总数为a人,绿地面积为b m2,那么该市人均拥
有绿地 m2.
2.如果某种水果的售价为每千克a 元,那么b元可以购买这种水果
千克.
同一个分式可以表示现实生活中不同的实际意义.
探索活动
探索活动
用具体的数值代替分式中的字母,按照分式中的运算关系计算,得到相应分式的值.
0
分式的值随分式中字母取值的变化而变化.
在这个分式中,a可以等于- 2吗?为什么?
不可以,当a=- 2时分母a+2=0.
在分式 中,若a=3 , 分式的值是______;
若a= , 分式的值是______.
探索活动
分式有意义 分母不为零.
分式 有意义,则_______.
分式无意义 分母为零.
分式 无意义,则_______.
探索活动
在分式 中,若a=3 ,分式的值是______.
0
在分式 中,若a=3 ,分式的值还等于0 吗?
不等于
分式值为零 分子为零且分母不为零.
例2.填空:
(1)当x_____时,分式 无意义;
(2)当x_____时,分式 有意义;
(3)当x_____时,分式 无意义;
(4)当x_____时,分式 有意义;
(5)当x_____时,分式 的值为零;
(6)当x_____时,分式 的值为零.
=0
≠1
=±3
<0
= -2
= -5
由2x=0解得x=0
由x-1≠0解得x ≠1
由 -9=0解得x =±3
巩固练习
1.下列各式,哪些是整式?哪些是分式?
1+x+y2-
① ② ③ ④ ⑤
整式是____________;分式是______________.
①、③
②、④、⑤
巩固练习
2.无论x取什么值,下列分式总有意义的是( )
A. B. C. D.
C
3.如果分式 的值为零,则x的值为( )
A. ±1 B. 1 C. - 2 D. -1
D
巩固练习
x -3 -2 -1 0 1 2 3
无意义
3.填表:
巩固练习
4.若分式 的值为正数,求n的取值范围.
巩固练习
5.已知 和 互为相反数,求分式
的值.
巩固练习
6.已知x= -2时分式 无意义,x=4时该分式值为零,
求a+b的值.
创设情境
探索活动
归纳条件
运用知识
生活实例
分式定义
得出结论
解决问题
课堂小结
形如 (A、B是整式,且B中含有字母,B≠0) 的式子,叫做分式.
用具体的数值代替分式中的字母,按照分式中的运算关系计算,得到相应分式的值.分式的值随分式中字母取值的变化而变化.
分式有意义的条件是分母不为零,分式无意义的条件是分母为零.
分式值为零的条件是分子为零且分母不为零.
谢谢大家,再见!
分式
创设情境
2.一块长方形玻璃的面积为2 m2,
如果长是3 m,那么宽是 m;
2 m2
如果宽是a m,那么长是 m.
1.如果某市人口总数为a人,绿地面积为b m2,那么该市
人均拥有绿地 m2.
创设情境
3.如果面积为a公顷、 b公顷的两块棉田分别产棉花m 千克、
n千克,那么这两块棉田平均每公顷产棉花 千克.
4.已知A、B两地的路程为s km,甲乙两人分别从A、B两
地同时出发相向而行,甲的速度是x km/h,乙的速度是
y km/h,那么经过______h两人相遇.
创设情境
5.小明用a元钱去购买练习本,原价每本b元,如果每本降
价1元,那么现在可以购买练习本 本.
这些代数式有什么共同的特征?
探索活动
形如 (A、B是整式,且B中含有字母,B≠0) 的式子,
叫做分式.
其中A叫做分式的分子,B叫做分式的分母.
A
B
探索活动
分式与整式有什么不同?
整式和分式统称有理式,即:
有理式
整式
分式
分母不含字母
分母含字母
分母含字母
单项式和多项式(分母中不含字母)
例1.判断下列代数式哪些是分式?哪些是整式?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
π不是字母
分式可以表示现实生活中的一些数量关系:
1.如果某市人口总数为a人,绿地面积为b m2,那么该市人均拥
有绿地 m2.
2.如果某种水果的售价为每千克a 元,那么b元可以购买这种水果
千克.
同一个分式可以表示现实生活中不同的实际意义.
探索活动
探索活动
用具体的数值代替分式中的字母,按照分式中的运算关系计算,得到相应分式的值.
0
分式的值随分式中字母取值的变化而变化.
在这个分式中,a可以等于- 2吗?为什么?
不可以,当a=- 2时分母a+2=0.
在分式 中,若a=3 , 分式的值是______;
若a= , 分式的值是______.
探索活动
分式有意义 分母不为零.
分式 有意义,则_______.
分式无意义 分母为零.
分式 无意义,则_______.
探索活动
在分式 中,若a=3 ,分式的值是______.
0
在分式 中,若a=3 ,分式的值还等于0 吗?
不等于
分式值为零 分子为零且分母不为零.
例2.填空:
(1)当x_____时,分式 无意义;
(2)当x_____时,分式 有意义;
(3)当x_____时,分式 无意义;
(4)当x_____时,分式 有意义;
(5)当x_____时,分式 的值为零;
(6)当x_____时,分式 的值为零.
=0
≠1
=±3
<0
= -2
= -5
由2x=0解得x=0
由x-1≠0解得x ≠1
由 -9=0解得x =±3
巩固练习
1.下列各式,哪些是整式?哪些是分式?
1+x+y2-
① ② ③ ④ ⑤
整式是____________;分式是______________.
①、③
②、④、⑤
巩固练习
2.无论x取什么值,下列分式总有意义的是( )
A. B. C. D.
C
3.如果分式 的值为零,则x的值为( )
A. ±1 B. 1 C. - 2 D. -1
D
巩固练习
x -3 -2 -1 0 1 2 3
无意义
3.填表:
巩固练习
4.若分式 的值为正数,求n的取值范围.
巩固练习
5.已知 和 互为相反数,求分式
的值.
巩固练习
6.已知x= -2时分式 无意义,x=4时该分式值为零,
求a+b的值.
创设情境
探索活动
归纳条件
运用知识
生活实例
分式定义
得出结论
解决问题
课堂小结
形如 (A、B是整式,且B中含有字母,B≠0) 的式子,叫做分式.
用具体的数值代替分式中的字母,按照分式中的运算关系计算,得到相应分式的值.分式的值随分式中字母取值的变化而变化.
分式有意义的条件是分母不为零,分式无意义的条件是分母为零.
分式值为零的条件是分子为零且分母不为零.
谢谢大家,再见!
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
