苏科版八年级下册 10.5 分式方程1 课件(19张)
文档属性
| 名称 | 苏科版八年级下册 10.5 分式方程1 课件(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 426.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-06 11:37:00 | ||
图片预览






文档简介
(共19张PPT)
分式方程(1)
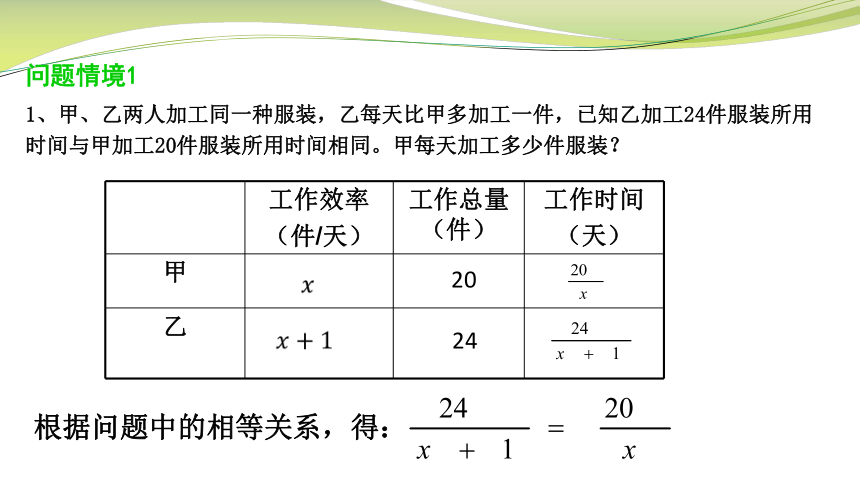
1、甲、乙两人加工同一种服装,乙每天比甲多加工一件,已知乙加工24件服装所用时间与甲加工20件服装所用时间相同。甲每天加工多少件服装?
工作效率
(件/天) 工作总量(件) 工作时间
(天)
甲
乙
20
24
根据问题中的相等关系,得:
问题情境1
2、一个两位数的个位数字是4,如果把个位数字与十位数字对调,那么所得的两位数与原来的两位数的比值是 , 原两位数字的十位字是几?
4
4
于是可得方程:
原两位数
改变后的两位数
问题情境2
3、某校学生到距离学校15km的山坡上植树,一部分学生骑自行车出发40min后,另一部分学生乘汽车出发,结果全体学生同时到达。已知汽车的速度是自行车速度的3倍,求自行车的速度。
自行车 汽车
路程 速度 时间 路程 速度 时间
15km 15km
km/h
km/h
根据时间的关系,汽车比自行车少用40分钟可以得到:
问题情境3
这些方程与一元一次方程有什么区别?
一元一次方程的未知数都在分子的位置上,而这些方程的未知数都在分母上。
讨论
分式方程(1)
★ 分式方程:
分母中含有未知数
★ 以前熟悉的方程(如一元一次方程):
分母中无未知数(或没有分母)
下列方程中,不是分式方程的是( )
C
(A)
(B)
(C)
(D)
这样“去分母”对吗?
2.怎样解下列分式方程?
1.怎样解下列方程?
去分母
去分母
两边都乘以分母的最小公倍数 6
“去分母”的依据是什么?
方程两边同乘最简公分母x(x+1)
让我们都来动手试一试!!!
探索
求分式方程的解,只要在方程的两边同乘各分式的最简公分母,有时就可以将分式方程转化成一元一次方程来解。
“转化”数学思想
解:
方程两边同乘,得
解这个方程,得
检验:
将 代入原方程的左、右两边,
注意:解分式方程一定要检验.
例1:解方程:
∵ 左边=,右边=,
左边=右边,
∴ x = 6 是原方程的解.
分母不能等于0
下列各分式方程,去分母时要乘以的式子分别是什么?
不要忘记“-1”!
通常是“最简公分母”
解:
方程两边同乘 ,得
解这个方程,得
检验:
将 y = -2 代入原方程的左、右两边,
例2. 解方程:
∵ 左边= ,右边= ,
左边=右边,
∴ y = -2 是原方程的解.
原方程可化为
1.在方程的两边都乘以最简公分母,约去分母,化成整式方程.
一化二解三检验
解分式方程的一般步骤
2.解这个整式方程.
3.把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.
4、写出原方程的根.
解分式方程一定要检验
解:方程两边同乘最简公分母
得整式方程
解得
检验:将代入原分式方程
相应的分式无意义,因此不是分式方程的解,此分式方程无解
其分母:
试一试
解下列方程:
练一练
答案:(1)
答案:(2)
你有哪些收获?
分式方程:分母中含有未知数
分式方程通过去分母化为熟悉的方程(如一元一次方程)
解分式方程一定要检验
1.在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2.解这个整式方程.
3.把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.
4、写出原方程的根.
一化二解三检验
解分式方程的一般步骤
谢 谢
分式方程(1)
1、甲、乙两人加工同一种服装,乙每天比甲多加工一件,已知乙加工24件服装所用时间与甲加工20件服装所用时间相同。甲每天加工多少件服装?
工作效率
(件/天) 工作总量(件) 工作时间
(天)
甲
乙
20
24
根据问题中的相等关系,得:
问题情境1
2、一个两位数的个位数字是4,如果把个位数字与十位数字对调,那么所得的两位数与原来的两位数的比值是 , 原两位数字的十位字是几?
4
4
于是可得方程:
原两位数
改变后的两位数
问题情境2
3、某校学生到距离学校15km的山坡上植树,一部分学生骑自行车出发40min后,另一部分学生乘汽车出发,结果全体学生同时到达。已知汽车的速度是自行车速度的3倍,求自行车的速度。
自行车 汽车
路程 速度 时间 路程 速度 时间
15km 15km
km/h
km/h
根据时间的关系,汽车比自行车少用40分钟可以得到:
问题情境3
这些方程与一元一次方程有什么区别?
一元一次方程的未知数都在分子的位置上,而这些方程的未知数都在分母上。
讨论
分式方程(1)
★ 分式方程:
分母中含有未知数
★ 以前熟悉的方程(如一元一次方程):
分母中无未知数(或没有分母)
下列方程中,不是分式方程的是( )
C
(A)
(B)
(C)
(D)
这样“去分母”对吗?
2.怎样解下列分式方程?
1.怎样解下列方程?
去分母
去分母
两边都乘以分母的最小公倍数 6
“去分母”的依据是什么?
方程两边同乘最简公分母x(x+1)
让我们都来动手试一试!!!
探索
求分式方程的解,只要在方程的两边同乘各分式的最简公分母,有时就可以将分式方程转化成一元一次方程来解。
“转化”数学思想
解:
方程两边同乘,得
解这个方程,得
检验:
将 代入原方程的左、右两边,
注意:解分式方程一定要检验.
例1:解方程:
∵ 左边=,右边=,
左边=右边,
∴ x = 6 是原方程的解.
分母不能等于0
下列各分式方程,去分母时要乘以的式子分别是什么?
不要忘记“-1”!
通常是“最简公分母”
解:
方程两边同乘 ,得
解这个方程,得
检验:
将 y = -2 代入原方程的左、右两边,
例2. 解方程:
∵ 左边= ,右边= ,
左边=右边,
∴ y = -2 是原方程的解.
原方程可化为
1.在方程的两边都乘以最简公分母,约去分母,化成整式方程.
一化二解三检验
解分式方程的一般步骤
2.解这个整式方程.
3.把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.
4、写出原方程的根.
解分式方程一定要检验
解:方程两边同乘最简公分母
得整式方程
解得
检验:将代入原分式方程
相应的分式无意义,因此不是分式方程的解,此分式方程无解
其分母:
试一试
解下列方程:
练一练
答案:(1)
答案:(2)
你有哪些收获?
分式方程:分母中含有未知数
分式方程通过去分母化为熟悉的方程(如一元一次方程)
解分式方程一定要检验
1.在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2.解这个整式方程.
3.把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.
4、写出原方程的根.
一化二解三检验
解分式方程的一般步骤
谢 谢
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
