苏科版八年级下册10.5 分式方程3 课件(20张)
文档属性
| 名称 | 苏科版八年级下册10.5 分式方程3 课件(20张) |  | |
| 格式 | zip | ||
| 文件大小 | 546.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-06 11:41:30 | ||
图片预览








文档简介
(共20张PPT)
分式方程(3)
1、列方程(组)解应用题的一般步骤是什么?
(1)根据题意设末知数
(2)分析题意寻找等量关系,列方程
(3)解所列方程;
(4)检验所列方程的解是否符合题意;
(5)写出完整的答案。
2、列方程(组)解应用题的关键是什么?
分析题意寻找等量关系,列方程。
回顾复习
京沪铁路是我国东部沿海地区纵南北的大动脉,全长1462km,是我国最繁忙的干线之一.如果货运列车的速度为km/h,快速列车的速度是货运列车的2倍,那么:
(1)货运列车从北京到上海需要___小时;
(2)快速列车从北京到上海需要____小时;
(3)已知从北京到上海快速列车比货运列车少用12h,你能列出一个方程吗?
例1.为迎接市中学生田径运动会,计划由某校八年级(1)班的3个小组制作240面彩旗,后因一个小组另有任务,改由另外两个小组完成制作彩旗的任务.这样,这两个小组的每个同学就要比原计划多做4面.如果这3个小组的人数相等,那么每个小组有多少名学生?
想一想:怎样确立等量关系呢?
工作人数 工作总量 人均工作量
计划(前)
计划(后)
3个小组
(名)
2个小组
(名)
240
240
例1.为迎接市中学生田径运动会,计划由某校八年级(1)班的3个小组制作240面彩旗,后因一个小组另有任务,改由另外两个小组完成制作彩旗的任务.这样,这两个小组的每个同学就要比原计划多做4面.如果这3个小组的人数相等,那么每个小组有多少名学生?
第三组量为等量
解这个方程,得
经检验,是原方程的根.
答:每组有10名同学.
根据题意,得
解:设每个小组有名学生.
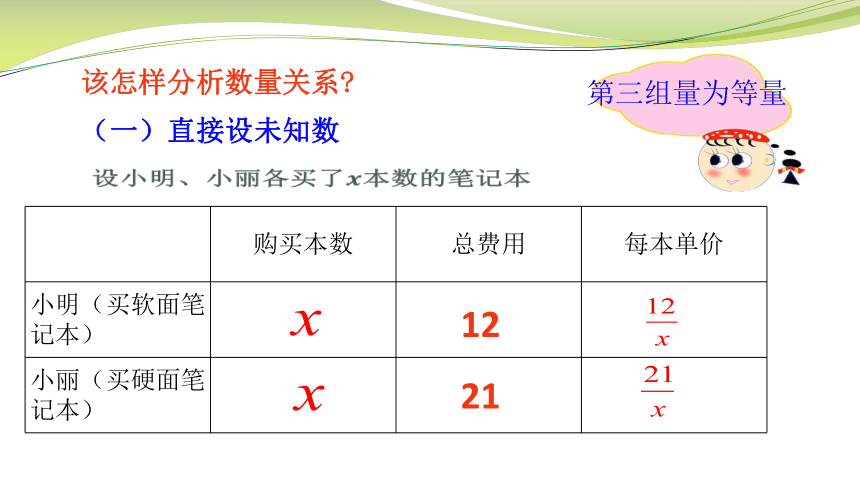
例2.小明买软面笔记本共用去12元,小丽买硬面笔记本共用去21元.已知每本硬面笔记本比软面笔记本贵1.2元,小明和小丽能买到相同本数的笔记本吗?
购买本数 总费用 每本单价
小明(买软面笔记本)
小丽(买硬面笔记本)
该怎样分析数量关系?
设小明、小丽各买了本数的笔记本
(一)直接设未知数
12
21
第三组量为等量
解这个方程,得
但由于笔记本的本数为7.5本,这不合实际意义.
答:小明和小丽不可能买到相同本数的笔记本.
经检验:是原方程的根.
解:设小明、小丽各买了 本数的笔记本.
根据题意,得
检验
“2”次
每本单价 总费用 购买本数
小明(买软面笔记本)
小丽(买硬面笔记本)
(二)间接设未知数
设软面笔记本每本元.
21
12
例2.小明买软面笔记本共用去12元,小丽买硬面笔记本共用去21元.已知每本硬面笔记本比软面笔记本贵1.2元,小明和小丽能买到相同本数的笔记本吗?
第三组量为等量
根据题意,得
解这个方程,得
但按此价格,笔记本的本数为7.5本,这不合实际意义.
答:小明和小丽不可能买到相同本数的笔记本
经检验:原分式方程的根.
解:设软面笔记本每本元.
检验
“2”次
(一般求什么设什么---这是直接设,也可间接设)
列分式方程解应用题步骤为:
1审
(审题,找出等量关系)
2设
3列
(根据等量关系列出方程)
4解
6答
5验
(既要验是否为所列分式方程的根,
又要验是否符合实际情况)
检验
“2”次
小结
(解这个方程)
(完整地写出答案,注意单位)
第三组量为等量
分析:这是一个经济问题
1、甲、乙两公司各为“见义勇为基金会”捐款30000元,已知乙公司比甲公司人均多捐款20元,且甲公司的人数比乙公司的人数多20%。问甲、乙两公司各有多少人?
①乙人均捐款额=甲人均捐款额+20
②甲人数=乙人数(1+ 20% )
捐款总额 人数 人均捐款额
甲
乙
30000
30000
练一练
等量关系
第三组量为等量
①乙人均捐款额=甲人均捐款额+20
②甲人数=乙人数(1+ 20% )
捐款总额 人数 人均捐款额
甲
乙
30000
30000
解:设乙公司有人,则甲公司有人,由题意得:
等量关系
第三组量为等量
分析:这是一个工程问题
2、甲乙两个工厂分别加工960件产品,已知乙工厂每天加工的件数比甲工厂多50%,而甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用20天,甲乙两个工厂每天加工该产品多少件
①乙工作效率=甲工作效率(1+50%)
②甲天=乙天+20
工作总量 工作效率 工作时间
甲
乙
960
960
等量关系
第三组量为等量
①乙工作效率=甲工作效率(1+50%)
②甲天=乙天+20
工作总量 工作效率 工作时间
甲
乙
960
960
解:设甲工厂每天生产个,则乙工厂每天生产,由题意得:
等量关系
第三组量为等量
分式方程的应用
工程问题
…
经济问题
路程问题
1、运用列表分析,假设未知数为第一组已知量
2、题目中已知量为第二组已知量
3、剩余第三组量为等量,用未知数的代数式表示后转化方程
3、为了绿化荒山,某村计划在荒山上种植1200棵树.原计划每天种棵,由于邻村的支援,每天比原计划多种了40棵,结果提前了5天完成了任务,则可以列出的方程为( )
1、列方程解决实际问题是很好的一条路径,关键要分清题意,找准相等关系.(第三量为等量)
2、解分式方程不要忘记检验!(检验增根)
3、有时,根据实际问题列出的分式方程虽然有解,但所求得的解有符合实际意义,所以这个问题无解.(二次)
你有哪些收获呢?
谢 谢
分式方程(3)
1、列方程(组)解应用题的一般步骤是什么?
(1)根据题意设末知数
(2)分析题意寻找等量关系,列方程
(3)解所列方程;
(4)检验所列方程的解是否符合题意;
(5)写出完整的答案。
2、列方程(组)解应用题的关键是什么?
分析题意寻找等量关系,列方程。
回顾复习
京沪铁路是我国东部沿海地区纵南北的大动脉,全长1462km,是我国最繁忙的干线之一.如果货运列车的速度为km/h,快速列车的速度是货运列车的2倍,那么:
(1)货运列车从北京到上海需要___小时;
(2)快速列车从北京到上海需要____小时;
(3)已知从北京到上海快速列车比货运列车少用12h,你能列出一个方程吗?
例1.为迎接市中学生田径运动会,计划由某校八年级(1)班的3个小组制作240面彩旗,后因一个小组另有任务,改由另外两个小组完成制作彩旗的任务.这样,这两个小组的每个同学就要比原计划多做4面.如果这3个小组的人数相等,那么每个小组有多少名学生?
想一想:怎样确立等量关系呢?
工作人数 工作总量 人均工作量
计划(前)
计划(后)
3个小组
(名)
2个小组
(名)
240
240
例1.为迎接市中学生田径运动会,计划由某校八年级(1)班的3个小组制作240面彩旗,后因一个小组另有任务,改由另外两个小组完成制作彩旗的任务.这样,这两个小组的每个同学就要比原计划多做4面.如果这3个小组的人数相等,那么每个小组有多少名学生?
第三组量为等量
解这个方程,得
经检验,是原方程的根.
答:每组有10名同学.
根据题意,得
解:设每个小组有名学生.
例2.小明买软面笔记本共用去12元,小丽买硬面笔记本共用去21元.已知每本硬面笔记本比软面笔记本贵1.2元,小明和小丽能买到相同本数的笔记本吗?
购买本数 总费用 每本单价
小明(买软面笔记本)
小丽(买硬面笔记本)
该怎样分析数量关系?
设小明、小丽各买了本数的笔记本
(一)直接设未知数
12
21
第三组量为等量
解这个方程,得
但由于笔记本的本数为7.5本,这不合实际意义.
答:小明和小丽不可能买到相同本数的笔记本.
经检验:是原方程的根.
解:设小明、小丽各买了 本数的笔记本.
根据题意,得
检验
“2”次
每本单价 总费用 购买本数
小明(买软面笔记本)
小丽(买硬面笔记本)
(二)间接设未知数
设软面笔记本每本元.
21
12
例2.小明买软面笔记本共用去12元,小丽买硬面笔记本共用去21元.已知每本硬面笔记本比软面笔记本贵1.2元,小明和小丽能买到相同本数的笔记本吗?
第三组量为等量
根据题意,得
解这个方程,得
但按此价格,笔记本的本数为7.5本,这不合实际意义.
答:小明和小丽不可能买到相同本数的笔记本
经检验:原分式方程的根.
解:设软面笔记本每本元.
检验
“2”次
(一般求什么设什么---这是直接设,也可间接设)
列分式方程解应用题步骤为:
1审
(审题,找出等量关系)
2设
3列
(根据等量关系列出方程)
4解
6答
5验
(既要验是否为所列分式方程的根,
又要验是否符合实际情况)
检验
“2”次
小结
(解这个方程)
(完整地写出答案,注意单位)
第三组量为等量
分析:这是一个经济问题
1、甲、乙两公司各为“见义勇为基金会”捐款30000元,已知乙公司比甲公司人均多捐款20元,且甲公司的人数比乙公司的人数多20%。问甲、乙两公司各有多少人?
①乙人均捐款额=甲人均捐款额+20
②甲人数=乙人数(1+ 20% )
捐款总额 人数 人均捐款额
甲
乙
30000
30000
练一练
等量关系
第三组量为等量
①乙人均捐款额=甲人均捐款额+20
②甲人数=乙人数(1+ 20% )
捐款总额 人数 人均捐款额
甲
乙
30000
30000
解:设乙公司有人,则甲公司有人,由题意得:
等量关系
第三组量为等量
分析:这是一个工程问题
2、甲乙两个工厂分别加工960件产品,已知乙工厂每天加工的件数比甲工厂多50%,而甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用20天,甲乙两个工厂每天加工该产品多少件
①乙工作效率=甲工作效率(1+50%)
②甲天=乙天+20
工作总量 工作效率 工作时间
甲
乙
960
960
等量关系
第三组量为等量
①乙工作效率=甲工作效率(1+50%)
②甲天=乙天+20
工作总量 工作效率 工作时间
甲
乙
960
960
解:设甲工厂每天生产个,则乙工厂每天生产,由题意得:
等量关系
第三组量为等量
分式方程的应用
工程问题
…
经济问题
路程问题
1、运用列表分析,假设未知数为第一组已知量
2、题目中已知量为第二组已知量
3、剩余第三组量为等量,用未知数的代数式表示后转化方程
3、为了绿化荒山,某村计划在荒山上种植1200棵树.原计划每天种棵,由于邻村的支援,每天比原计划多种了40棵,结果提前了5天完成了任务,则可以列出的方程为( )
1、列方程解决实际问题是很好的一条路径,关键要分清题意,找准相等关系.(第三量为等量)
2、解分式方程不要忘记检验!(检验增根)
3、有时,根据实际问题列出的分式方程虽然有解,但所求得的解有符合实际意义,所以这个问题无解.(二次)
你有哪些收获呢?
谢 谢
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
