5.5确定二次函数的表达式(二次函数的几种解析式及求法) 课件(共12张PPT)
文档属性
| 名称 | 5.5确定二次函数的表达式(二次函数的几种解析式及求法) 课件(共12张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 751.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-07 00:00:00 | ||
图片预览




文档简介
(共12张PPT)
练习1
练习2
思想方法
应用举例
一般式
顶点式
交点式
例1
练习
二次函数的几种解析式及求法
前 言
二次函数解析式
练习3
小 结
平移式
例2 平移式
复习二次函数四种平移关系
一、二次函数常用的几种解析式的确定
已知抛物线上三点的坐标,通常选择一般式。
已知抛物线上顶点坐标(对称轴或最值),通常选择顶点式。
已知抛物线与x轴的交点坐标或对称轴,选择交点式。
1、一般式
2、顶点式
3、交点式
4、平移式
将抛物线平移,函数解析式中发生变化的只有顶点坐标, 可将原函数用顶点式表示,再根据“左加右减,上加下减“的法则,即可得出所求新函数的解析式。
例1、已知二次函数 的图像如图所示,
求其解析式。
解法一: 一般式
设解析式为
∵顶点C(1,4),
∴对称轴 x=1.
∵A(-1,0)关于 x=1对称,
∴B(3,0)。
∵A(-1,0)、B(3,0)和
C(1,4)在抛物线上,
∴
即:
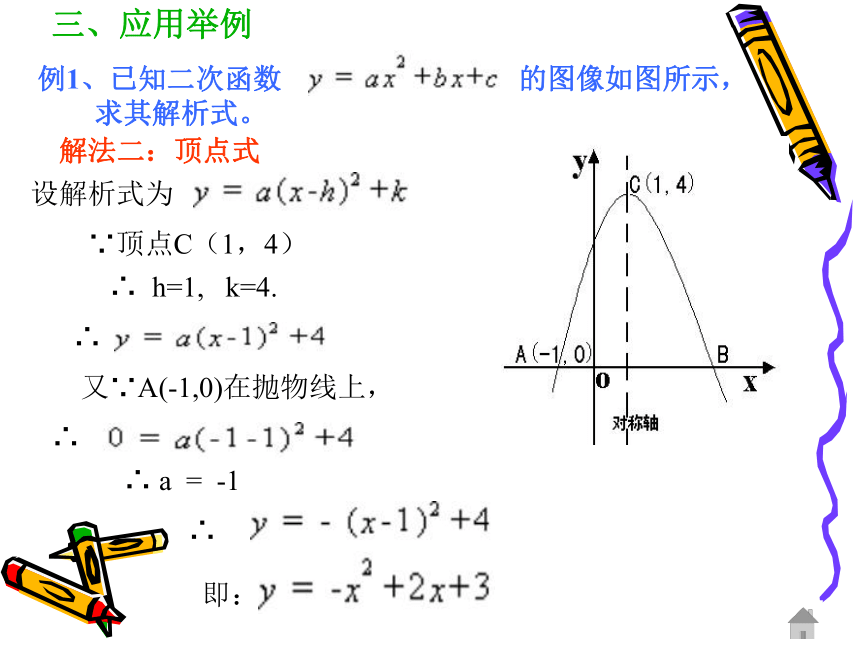
三、应用举例
例1、已知二次函数 的图像如图所示,
求其解析式。
解法二:顶点式
设解析式为
∵顶点C(1,4)
∴
又∵A(-1,0)在抛物线上,
∴
∴ a = -1
即:
∴
∴ h=1, k=4.
三、应用举例
解法三:交点式
设解析式为
∵抛物线与x 轴的两个交点坐标
为 A (-1,0)、B(3,0)
∴ y = a (x+1) (x- 3)
又 C(1,4)在抛物线上
∴ 4 = a (1+1) (1-3)
∴ a = -1
∴ y = - ( x+1) (x-3)
即:
例1、已知二次函数 的图像如图所示,
求其解析式。
三、应用举例
例2、将抛物线 向左平移4个单位,
再向下平移3个单位,求平移后所得抛物线的解析式。
解法:将二次函数的解析式
转化为顶点式得:
(1)、由 向左平移4个单位得:
(左加右减)
(2)、再将 向下平移3个单位得
(上加下减)
即:所求的解析式为
二、应用举例
1、已知二次函数的图像过原点,当x=1时,y有最小值为
-1,求其解析式。
∴
三、尝试练习
解:设二次函数的解析式为
∵ x = 1, y= -1 , ∴顶点(1,-1)。
又(0,0)在抛物线上,
∴ a = 1
即:
∴
∴
2、已知二次函数与x 轴的交点坐标为(-1,0),(1,0),点(0,1)在图像上,求其解析式。
解:设所求的解析式为
∵抛物线与x轴的交点坐标为(-1,0)、(1,0)
∴
又∵点(0,1)在图像上,
∴ a = -1
即:
∴
∴
∴
三、尝试练习
3、如图;有一个抛物线形的隧道桥拱,这个桥拱的最大高度为3.6m,跨度为7.2m.一辆卡车车高3米,宽1.6米,它能否通过隧道?
四、尝试应用练习
即当x= OC=1.6÷2=0.8米时,过C点作CD⊥AB交抛物线于D点,若y=CD≥3米,则卡车可以通过。
分析:卡车能否通过,只要看卡车在隧道正中间时,其车高3米是否超过其位置的拱高。
五、小结
1、二次函数常用解析式
.已知图象上三点坐标,通常选择一般式。
.已知图象的顶点坐标(对称轴或最值),通常选择顶点式。
.已知图象与x轴的两个交点的横坐标x1、x2, 通常选择交点式。
3. 确定二次函数的解析式的关键是根据条件的特点,恰当地选择一种函数表达式,灵活应用。
一般式
顶点式
交点式
2、求二次函数解析式的一般方法:
已知图象中发生变化的只有顶点坐标,通常选择平移式。
平移式
谢谢!
练习1
练习2
思想方法
应用举例
一般式
顶点式
交点式
例1
练习
二次函数的几种解析式及求法
前 言
二次函数解析式
练习3
小 结
平移式
例2 平移式
复习二次函数四种平移关系
一、二次函数常用的几种解析式的确定
已知抛物线上三点的坐标,通常选择一般式。
已知抛物线上顶点坐标(对称轴或最值),通常选择顶点式。
已知抛物线与x轴的交点坐标或对称轴,选择交点式。
1、一般式
2、顶点式
3、交点式
4、平移式
将抛物线平移,函数解析式中发生变化的只有顶点坐标, 可将原函数用顶点式表示,再根据“左加右减,上加下减“的法则,即可得出所求新函数的解析式。
例1、已知二次函数 的图像如图所示,
求其解析式。
解法一: 一般式
设解析式为
∵顶点C(1,4),
∴对称轴 x=1.
∵A(-1,0)关于 x=1对称,
∴B(3,0)。
∵A(-1,0)、B(3,0)和
C(1,4)在抛物线上,
∴
即:
三、应用举例
例1、已知二次函数 的图像如图所示,
求其解析式。
解法二:顶点式
设解析式为
∵顶点C(1,4)
∴
又∵A(-1,0)在抛物线上,
∴
∴ a = -1
即:
∴
∴ h=1, k=4.
三、应用举例
解法三:交点式
设解析式为
∵抛物线与x 轴的两个交点坐标
为 A (-1,0)、B(3,0)
∴ y = a (x+1) (x- 3)
又 C(1,4)在抛物线上
∴ 4 = a (1+1) (1-3)
∴ a = -1
∴ y = - ( x+1) (x-3)
即:
例1、已知二次函数 的图像如图所示,
求其解析式。
三、应用举例
例2、将抛物线 向左平移4个单位,
再向下平移3个单位,求平移后所得抛物线的解析式。
解法:将二次函数的解析式
转化为顶点式得:
(1)、由 向左平移4个单位得:
(左加右减)
(2)、再将 向下平移3个单位得
(上加下减)
即:所求的解析式为
二、应用举例
1、已知二次函数的图像过原点,当x=1时,y有最小值为
-1,求其解析式。
∴
三、尝试练习
解:设二次函数的解析式为
∵ x = 1, y= -1 , ∴顶点(1,-1)。
又(0,0)在抛物线上,
∴ a = 1
即:
∴
∴
2、已知二次函数与x 轴的交点坐标为(-1,0),(1,0),点(0,1)在图像上,求其解析式。
解:设所求的解析式为
∵抛物线与x轴的交点坐标为(-1,0)、(1,0)
∴
又∵点(0,1)在图像上,
∴ a = -1
即:
∴
∴
∴
三、尝试练习
3、如图;有一个抛物线形的隧道桥拱,这个桥拱的最大高度为3.6m,跨度为7.2m.一辆卡车车高3米,宽1.6米,它能否通过隧道?
四、尝试应用练习
即当x= OC=1.6÷2=0.8米时,过C点作CD⊥AB交抛物线于D点,若y=CD≥3米,则卡车可以通过。
分析:卡车能否通过,只要看卡车在隧道正中间时,其车高3米是否超过其位置的拱高。
五、小结
1、二次函数常用解析式
.已知图象上三点坐标,通常选择一般式。
.已知图象的顶点坐标(对称轴或最值),通常选择顶点式。
.已知图象与x轴的两个交点的横坐标x1、x2, 通常选择交点式。
3. 确定二次函数的解析式的关键是根据条件的特点,恰当地选择一种函数表达式,灵活应用。
一般式
顶点式
交点式
2、求二次函数解析式的一般方法:
已知图象中发生变化的只有顶点坐标,通常选择平移式。
平移式
谢谢!
