高中物理人教版必修1课件 第二章 匀变速直线运动的研究 2.4 匀变速直线运动的速度与位移的关系1(共24张PPT)
文档属性
| 名称 | 高中物理人教版必修1课件 第二章 匀变速直线运动的研究 2.4 匀变速直线运动的速度与位移的关系1(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-06 13:37:10 | ||
图片预览







文档简介
(共24张PPT)
高中物理·必修1·人教版
第二章 匀变速直线运动的研究
2.4 匀变速直线运动的速度与位移的关系
掌握三个平均速度公式及其适用条件
3
1
会推导速度与位移的关系式,并知道匀变速直线运动的速度与位移的关系式中各物理量的含义
2
会用公式v2-v2 =2ax 进行分析和计算
4
会推导Δx =aT2 并会用它解决相关问题
0
匀变速直线运动的速度与位移关系式
1.公式:v2 - v2= 2ax
2.推导:物体以加速度a 做匀变速直线运动时,设其初
速度为v0 ,末速度为v,则由
速度公式:v = v0+at
位移公式:x = v0t+at2/2
消去时间 t 得位移与速度的关系式为 v2 – v2 = 2ax.
0
0
一. 速度位移公式的推导及应用
答案
【问题设计】
我国第一艘航空母舰“辽宁号”已有能力同时起飞3架歼15战机,如图
为辽宁舰上3个起飞点示意图,1、2号位置为短距起飞点,起飞线长
105米;3号位置为远距起飞点,起飞线长195 米.如果歼15 战机起飞
速度为50 m/s,起飞时航母静止不动,且不使用弹射系统,则战机由
3号起飞点起飞的加速度至少是多少?(设跑道水平)
根据v = v0+ at ① x = v0t + at2/2 ②
由①得 t = (v-v0)/a ③
把③代入②得
整理得:v2-v2=2ax
将v0= 0,v = 50 m/s,x = 195 m 代入上式得:a≈6.41 m/s2.
0
1.匀变速直线运动的位移速度公式:v2– v2= ,此式是矢量式,应用解题时一定要先选定正方向,并注意各量的符号.
若v0方向为正方向,则:
(1)物体做加速运动时,加速度a 取 ;
做减速运动时,加速度a 取 .
(2)位移x > 0说明物体通过的位移方向与初速度方向 ,
x < 0说明物体通过的位移方向与初速度方向
2.两种特殊情况
(1)当v0= 0时, .
(2)当v = 0时, .
3.公式特点:该公式不涉及 .
【要点提炼】
2ax
v2=2ax
-v2=2ax
正值
负值
相同
相反
时间
0
二 . 中间时刻的瞬时速度与平均速度
答案
【问题设计】
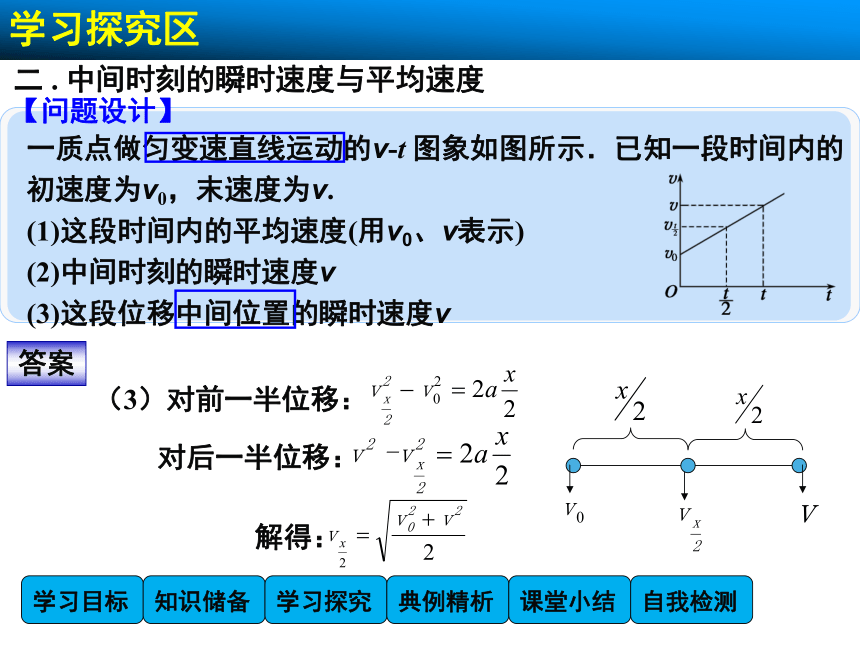
一质点做匀变速直线运动的v-t 图象如图所示.已知一段时间内的
初速度为v0,末速度为v.
(1)这段时间内的平均速度(用v0、v表示)
(2)中间时刻的瞬时速度
(3)这段位移中间位置的瞬时速度
(1)v-t 图像与t 轴所围面积表示位移
位移:
平均速度:
(2)由图中可知:中间时刻的瞬时
速度大小等于梯形中位线长度
位移/时间
二 . 中间时刻的瞬时速度与平均速度
答案
【问题设计】
一质点做匀变速直线运动的v-t 图象如图所示.已知一段时间内的
初速度为v0,末速度为v.
(1)这段时间内的平均速度(用v0、v表示)
(2)中间时刻的瞬时速度v
(3)这段位移中间位置的瞬时速度v
(3)对前一半位移:
对后一半位移:
解得:
【要点提炼】
1.中间时刻的瞬时速度
2.中间位置的瞬时速度
3.平均速度公式总结:
,适用条件: .
,适用条件: .
,适用条件: .
注意 对匀变速直线运动有
任意运动
匀变速直线运动
匀变速直线运动
【延伸思考】
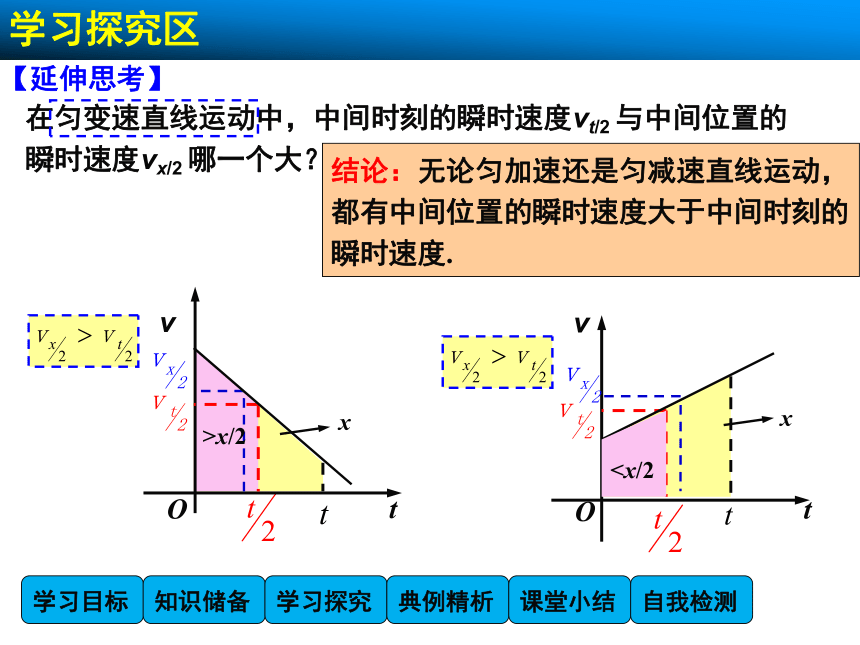
在匀变速直线运动中,中间时刻的瞬时速度vt/2 与中间位置的
瞬时速度vx/2 哪一个大?
t
O
v
t
O
v
x
x
>x/2
结论:无论匀加速还是匀减速直线运动,
都有中间位置的瞬时速度大于中间时刻的瞬时速度.
三 . 重要推论Δx =aT2 的推导及应用
证明
【问题设计】
物体做匀变速直线运动,加速度为a,从某时刻起T 时间内的位
移为x1,紧接着第二个T 时间内的位移为x2.试证明:x2-x1=aT2.
设物体的初速度为v0
自计时起T 时间内的位移 x1= v0T+aT2/2 ①
在第2个T时间内的位移
x2= v0·2T+a(2T)2/2-x1= v0T+3aT2/2 ②
由①②两式得连续相等时间内的位移差为
Δx= x2 - x1= v0T +3aT2/2- v0T-aT2/2 = aT2
即Δx = aT2.
【要点提炼】
1.匀变速直线运动中,在连续相等的时间T 内的位移之差为一恒定值, 即Δx =_________.
2.应用
(1)判断物体是否做匀变速直线运动
如果Δx = x2 - x1 = x3 - x2 = ……= xn- xn-1= aT2 成立,
则a 为一恒量,说明物体做匀变速直线运动.
(2) 求加速度
利用连续相等时间段内的位移差Δx,可求得a =
Δx/T2 .
aT2
解析
例1:A、B、C 三点在同一条
直线上,一物体从A 点由静止
开始做匀加速直线运动,经过
B 点的速度是v,到C 点的速度
是3v,则xAB∶xBC等于( )
A.1∶8
B.1∶6
C.1∶5
D.1∶3
A
速度—位移公式
从A到B:
从B到C:
初速度为0
例2:一质点做匀变速直线运动,初速度v0=2 m/s, 4 s内位移为
20 m,求:
(1)质点4 s末的速度
(2)质点2 s末的速度
解析
解法一:利用平均速度公式
4s末速度
2s末的速度
x=20m
解析
例2:一质点做匀变速直线运动,初速度v0=2 m/s, 4 s内位移为
20 m,求:
(1)质点4 s末的速度
(2)质点2 s末的速度
解法二:利用两个基本公式
由
解得:
由
解得:
4s末的速度
2s末的速度
x=20m
v0= 2 m/s
v2= ?
v4= ?
解析
一辆汽车从静止开始由甲地出发,沿平直公路开往乙地,汽车先做匀加速直线运动,接着做匀减速直线运动,开到乙地刚好停止,其速度—时间图象如图所示,那么0 ~t 和 t ~3t 两段时间内 ( )
A.加速度大小之比为3∶1
B.位移大小之比为1∶2
C.平均速度大小之比为2∶1
D.平均速度大小之比为1∶1
BD
v-t 图中面积:表示位移
v-t 图中斜率:表示加速度
解析
解法一:利用关系式Δx =aT2
前4s内的位移:
例3:做匀加速直线运动的物体,从开始计时起连续两个4 s的时
间间隔内通过的位移分别是48 m和80 m,则这个物体的初速度和
加速度各是多少?
解析
例3:做匀加速直线运动的物体,从开始计时起连续两个4 s的时
间间隔内通过的位移分别是48 m和80 m,则这个物体的初速度和
加速度各是多少?
解法二:利用两个基本公式
由
前4 s 内:
前8 s 内:
解得:
解析
解法三:利用平均速度公式
物体的加速度:
物体的初速度:
第2 s 时速度:
第6 s 时速度:
例3:做匀加速直线运动的物体,从开始计时起连续两个4 s的时
间间隔内通过的位移分别是48 m和80 m,则这个物体的初速度和
加速度各是多少?
解析
1.(速度与位移关系的简单应
用)两个小车在水平面上做
加速度相同的匀减速直线运
动,若它们的初速度之比为
1∶2,它们运动的最大位移
之比为( )
A.1∶2
B.1∶4
C.
D.2∶1
B
速度—位移公式
解析
2.( 的灵活应用)
汽车自O 点出发从静止开始在平直
公路上做匀加速直线运动,途中在
6 s 内分别经过P、Q 两根电线杆,
已知P、Q 电线杆相距60 m,车经过
电线杆Q 时的速率是15 m/s,则
下列说法正确的是( )
A.经过P 杆时的速率是5 m/s
B.车的加速度是1.5 m/s2
C.P、O 间的距离是7.5 m
D.车从出发到经过Q 所用的时间是
9 s
ACD
从P 到Q :
从O 到P :
从O 到Q :
O
P
Q
解析
3.(对Δx=aT2 的理解和应用)
从斜面上某一位置每隔0.1 s释放一个相同的小球,释放后小球做匀加速直线运动,在连续释放几个后,对在斜面上滚动的小球拍下如图所示的照片,测得xAB= 15 cm,xBC= 20 cm.试问:
(1)小球的加速度是多少?
(2)拍摄时小球B 的速度是多少?
(3)拍摄时xCD 是多少?
小球释放后做匀加速直线运动,且每相邻的两个小球的时间间隔相 等,均为0.1 s,可以认为A、B、C、D各点是一个小球在不同时刻的位置
(1)由推论Δx =aT2 ,小球的加速度
解析
(2)B 点对应AC 段的中间时刻,则B 点速度等于AC 段的
平均速度
(3)连续相等时间内位移差恒定
3.(对Δx=aT2 的理解和应用)
从斜面上某一位置每隔0.1 s释放一个相同的小球,释放后小球做匀加速直线运动,在连续释放几个后,对在斜面上滚动的小球拍下如图所示的照片,测得xAB= 15 cm,xBC= 20 cm.试问:
(1)小球的加速度是多少?
(2)拍摄时小球B 的速度是多少?
(3)拍摄时xCD 是多少?
再见
高中物理·必修1·人教版
第二章 匀变速直线运动的研究
2.4 匀变速直线运动的速度与位移的关系
掌握三个平均速度公式及其适用条件
3
1
会推导速度与位移的关系式,并知道匀变速直线运动的速度与位移的关系式中各物理量的含义
2
会用公式v2-v2 =2ax 进行分析和计算
4
会推导Δx =aT2 并会用它解决相关问题
0
匀变速直线运动的速度与位移关系式
1.公式:v2 - v2= 2ax
2.推导:物体以加速度a 做匀变速直线运动时,设其初
速度为v0 ,末速度为v,则由
速度公式:v = v0+at
位移公式:x = v0t+at2/2
消去时间 t 得位移与速度的关系式为 v2 – v2 = 2ax.
0
0
一. 速度位移公式的推导及应用
答案
【问题设计】
我国第一艘航空母舰“辽宁号”已有能力同时起飞3架歼15战机,如图
为辽宁舰上3个起飞点示意图,1、2号位置为短距起飞点,起飞线长
105米;3号位置为远距起飞点,起飞线长195 米.如果歼15 战机起飞
速度为50 m/s,起飞时航母静止不动,且不使用弹射系统,则战机由
3号起飞点起飞的加速度至少是多少?(设跑道水平)
根据v = v0+ at ① x = v0t + at2/2 ②
由①得 t = (v-v0)/a ③
把③代入②得
整理得:v2-v2=2ax
将v0= 0,v = 50 m/s,x = 195 m 代入上式得:a≈6.41 m/s2.
0
1.匀变速直线运动的位移速度公式:v2– v2= ,此式是矢量式,应用解题时一定要先选定正方向,并注意各量的符号.
若v0方向为正方向,则:
(1)物体做加速运动时,加速度a 取 ;
做减速运动时,加速度a 取 .
(2)位移x > 0说明物体通过的位移方向与初速度方向 ,
x < 0说明物体通过的位移方向与初速度方向
2.两种特殊情况
(1)当v0= 0时, .
(2)当v = 0时, .
3.公式特点:该公式不涉及 .
【要点提炼】
2ax
v2=2ax
-v2=2ax
正值
负值
相同
相反
时间
0
二 . 中间时刻的瞬时速度与平均速度
答案
【问题设计】
一质点做匀变速直线运动的v-t 图象如图所示.已知一段时间内的
初速度为v0,末速度为v.
(1)这段时间内的平均速度(用v0、v表示)
(2)中间时刻的瞬时速度
(3)这段位移中间位置的瞬时速度
(1)v-t 图像与t 轴所围面积表示位移
位移:
平均速度:
(2)由图中可知:中间时刻的瞬时
速度大小等于梯形中位线长度
位移/时间
二 . 中间时刻的瞬时速度与平均速度
答案
【问题设计】
一质点做匀变速直线运动的v-t 图象如图所示.已知一段时间内的
初速度为v0,末速度为v.
(1)这段时间内的平均速度(用v0、v表示)
(2)中间时刻的瞬时速度v
(3)这段位移中间位置的瞬时速度v
(3)对前一半位移:
对后一半位移:
解得:
【要点提炼】
1.中间时刻的瞬时速度
2.中间位置的瞬时速度
3.平均速度公式总结:
,适用条件: .
,适用条件: .
,适用条件: .
注意 对匀变速直线运动有
任意运动
匀变速直线运动
匀变速直线运动
【延伸思考】
在匀变速直线运动中,中间时刻的瞬时速度vt/2 与中间位置的
瞬时速度vx/2 哪一个大?
t
O
v
t
O
v
x
>x/2
结论:无论匀加速还是匀减速直线运动,
都有中间位置的瞬时速度大于中间时刻的瞬时速度.
三 . 重要推论Δx =aT2 的推导及应用
证明
【问题设计】
物体做匀变速直线运动,加速度为a,从某时刻起T 时间内的位
移为x1,紧接着第二个T 时间内的位移为x2.试证明:x2-x1=aT2.
设物体的初速度为v0
自计时起T 时间内的位移 x1= v0T+aT2/2 ①
在第2个T时间内的位移
x2= v0·2T+a(2T)2/2-x1= v0T+3aT2/2 ②
由①②两式得连续相等时间内的位移差为
Δx= x2 - x1= v0T +3aT2/2- v0T-aT2/2 = aT2
即Δx = aT2.
【要点提炼】
1.匀变速直线运动中,在连续相等的时间T 内的位移之差为一恒定值, 即Δx =_________.
2.应用
(1)判断物体是否做匀变速直线运动
如果Δx = x2 - x1 = x3 - x2 = ……= xn- xn-1= aT2 成立,
则a 为一恒量,说明物体做匀变速直线运动.
(2) 求加速度
利用连续相等时间段内的位移差Δx,可求得a =
Δx/T2 .
aT2
解析
例1:A、B、C 三点在同一条
直线上,一物体从A 点由静止
开始做匀加速直线运动,经过
B 点的速度是v,到C 点的速度
是3v,则xAB∶xBC等于( )
A.1∶8
B.1∶6
C.1∶5
D.1∶3
A
速度—位移公式
从A到B:
从B到C:
初速度为0
例2:一质点做匀变速直线运动,初速度v0=2 m/s, 4 s内位移为
20 m,求:
(1)质点4 s末的速度
(2)质点2 s末的速度
解析
解法一:利用平均速度公式
4s末速度
2s末的速度
x=20m
解析
例2:一质点做匀变速直线运动,初速度v0=2 m/s, 4 s内位移为
20 m,求:
(1)质点4 s末的速度
(2)质点2 s末的速度
解法二:利用两个基本公式
由
解得:
由
解得:
4s末的速度
2s末的速度
x=20m
v0= 2 m/s
v2= ?
v4= ?
解析
一辆汽车从静止开始由甲地出发,沿平直公路开往乙地,汽车先做匀加速直线运动,接着做匀减速直线运动,开到乙地刚好停止,其速度—时间图象如图所示,那么0 ~t 和 t ~3t 两段时间内 ( )
A.加速度大小之比为3∶1
B.位移大小之比为1∶2
C.平均速度大小之比为2∶1
D.平均速度大小之比为1∶1
BD
v-t 图中面积:表示位移
v-t 图中斜率:表示加速度
解析
解法一:利用关系式Δx =aT2
前4s内的位移:
例3:做匀加速直线运动的物体,从开始计时起连续两个4 s的时
间间隔内通过的位移分别是48 m和80 m,则这个物体的初速度和
加速度各是多少?
解析
例3:做匀加速直线运动的物体,从开始计时起连续两个4 s的时
间间隔内通过的位移分别是48 m和80 m,则这个物体的初速度和
加速度各是多少?
解法二:利用两个基本公式
由
前4 s 内:
前8 s 内:
解得:
解析
解法三:利用平均速度公式
物体的加速度:
物体的初速度:
第2 s 时速度:
第6 s 时速度:
例3:做匀加速直线运动的物体,从开始计时起连续两个4 s的时
间间隔内通过的位移分别是48 m和80 m,则这个物体的初速度和
加速度各是多少?
解析
1.(速度与位移关系的简单应
用)两个小车在水平面上做
加速度相同的匀减速直线运
动,若它们的初速度之比为
1∶2,它们运动的最大位移
之比为( )
A.1∶2
B.1∶4
C.
D.2∶1
B
速度—位移公式
解析
2.( 的灵活应用)
汽车自O 点出发从静止开始在平直
公路上做匀加速直线运动,途中在
6 s 内分别经过P、Q 两根电线杆,
已知P、Q 电线杆相距60 m,车经过
电线杆Q 时的速率是15 m/s,则
下列说法正确的是( )
A.经过P 杆时的速率是5 m/s
B.车的加速度是1.5 m/s2
C.P、O 间的距离是7.5 m
D.车从出发到经过Q 所用的时间是
9 s
ACD
从P 到Q :
从O 到P :
从O 到Q :
O
P
Q
解析
3.(对Δx=aT2 的理解和应用)
从斜面上某一位置每隔0.1 s释放一个相同的小球,释放后小球做匀加速直线运动,在连续释放几个后,对在斜面上滚动的小球拍下如图所示的照片,测得xAB= 15 cm,xBC= 20 cm.试问:
(1)小球的加速度是多少?
(2)拍摄时小球B 的速度是多少?
(3)拍摄时xCD 是多少?
小球释放后做匀加速直线运动,且每相邻的两个小球的时间间隔相 等,均为0.1 s,可以认为A、B、C、D各点是一个小球在不同时刻的位置
(1)由推论Δx =aT2 ,小球的加速度
解析
(2)B 点对应AC 段的中间时刻,则B 点速度等于AC 段的
平均速度
(3)连续相等时间内位移差恒定
3.(对Δx=aT2 的理解和应用)
从斜面上某一位置每隔0.1 s释放一个相同的小球,释放后小球做匀加速直线运动,在连续释放几个后,对在斜面上滚动的小球拍下如图所示的照片,测得xAB= 15 cm,xBC= 20 cm.试问:
(1)小球的加速度是多少?
(2)拍摄时小球B 的速度是多少?
(3)拍摄时xCD 是多少?
再见
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
