鲁教版八年级数学下册第六章特殊平行四边形测试题(含答案)
文档属性
| 名称 | 鲁教版八年级数学下册第六章特殊平行四边形测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 275.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-06 14:39:14 | ||
图片预览

文档简介
第六章 特殊平行四边形测试题
1、选择题(每小题3分,共30分)
1.下列说法不正确的是( )
A.对角线互相垂直的矩形是正方形 B.对角线相等的菱形是正方形
C.有一个角是直角的平行四边形是正方形 D.邻边相等的矩形是正方形
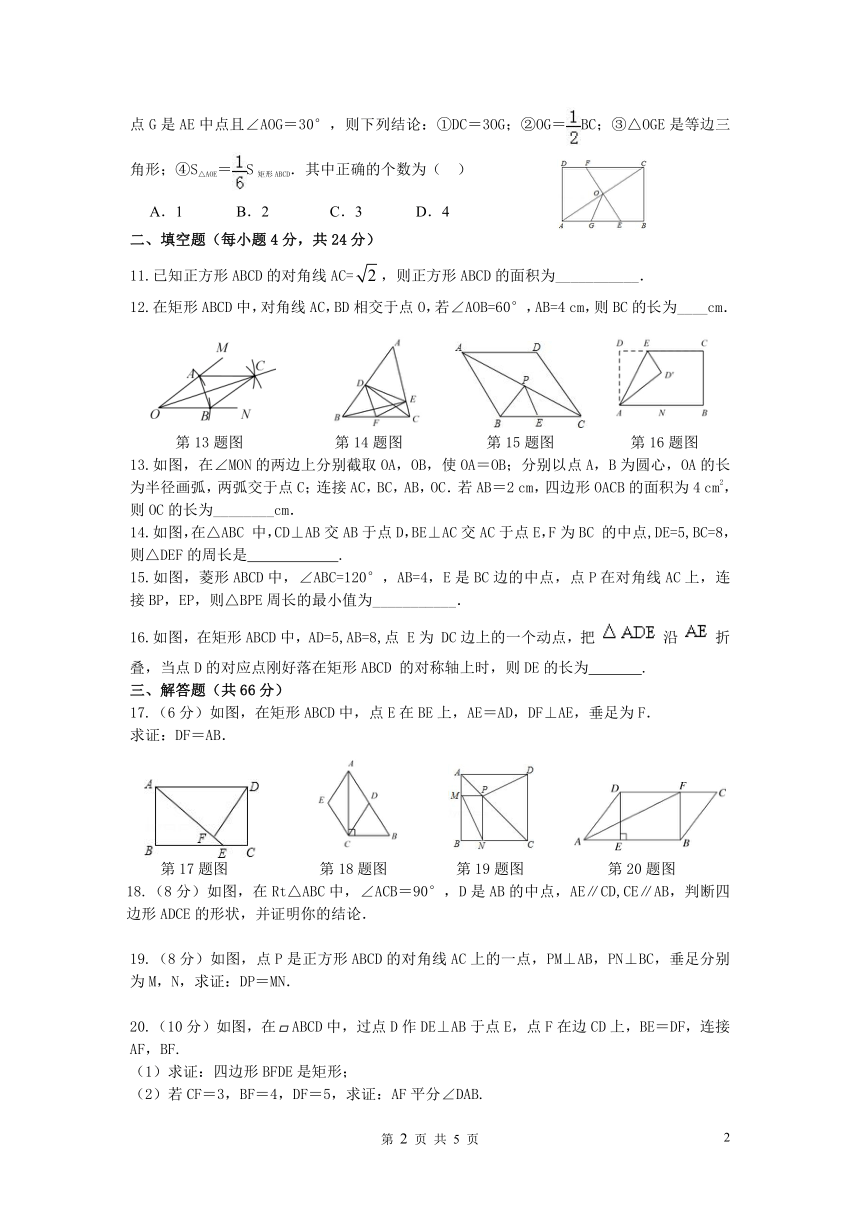
2.如图,把一张矩形纸片ABCD沿EF折叠后,点C,D分别落在C′,D′的位置上,EC′交AD于点G.若∠EFG=58°,则∠FEG的度数是( )
A. 58° B. 60° C. 45° D. 30°
第2题图 第3题图 第4题图 第5题图
3.如图,把一张矩形纸片对折两次,然后剪下一个角并打开,剪出的纸片形状一定是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
4.如图,在Rt△ABC中,CD是斜边AB上的中线,若∠A=20°,则∠BDC的度数为( )
A.30° B.40° C.45° D.60°
5.如图,菱形ABCD的周长是20,对角线AC,BD相交于点O,若BD=6,则菱形ABCD的面积是( )
A.6 B.12 C.24 D.48
第第6题图 第7题图 第8题图 第9题图
6.如图,过正方形ABCD的顶点B作直线l,过A,C作直线l的垂线,垂足分别为E,F,若AE=1,CF=3,则AB的长为( )
A. B.10 C.3 D.
7.如图,在△ABC中,D是BC边上的点(与 B,C两点不重合),过点D 作DE∥AC,DF∥AB, 分别交 AB,AC于 E,F 两点,下列说法正确的是( )
A. 若 AD⊥BC,则四边形 AEDF 是矩形 B. 若 AD垂直平分 BC,则四边形AEDF 是矩形
C. 若 BD=CD,则四边形 AEDF 是菱形 D. 若 AD 平分 ∠BAC,则四边形AEDF是菱形
8.如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
A.10 B.12 C.18 D.24
9.如图,在正方形ABCD的外侧作等边三角形ADE,连接BE交AD于点F,则∠DFE的度数为( )
A. 45° B. 55° C. 60° D. 75°
10.如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于E,点G是AE中点且∠AOG=30°,则下列结论:①DC=3OG;②OG=BC;③△OGE是等边三角形;④S△AOE=S矩形ABCD.其中正确的个数为( )
A.1 B.2 C.3 D.4 第10题图
2、填空题(每小题4分,共24分)
11.已知正方形ABCD的对角线AC=,则正方形ABCD的面积为___________.
12.在矩形ABCD中,对角线AC,BD相交于点O,若∠AOB=60°,AB=4 cm,则BC的长为____cm.
第13题图 第14题图 第15题图 第16题图
13.如图,在∠MON的两边上分别截取OA,OB,使OA=OB;分别以点A,B为圆心,OA的长为半径画弧,两弧交于点C;连接AC,BC,AB,OC.若AB=2 cm,四边形OACB的面积为4 cm2,则OC的长为________cm.
14.如图,在△ABC 中,CD⊥AB交AB于点D,BE⊥AC交AC于点E,F为BC 的中点,DE=5,BC=8,则△DEF的周长是 .
15.如图,菱形ABCD中,∠ABC=120°,AB=4,E是BC边的中点,点P在对角线AC上,连接BP,EP,则△BPE周长的最小值为___________.
16.如图,在矩形ABCD中,AD=5,AB=8,点 E为 DC边上的一个动点,把 沿 折叠,当点D的对应点刚好落在矩形ABCD 的对称轴上时,则DE的长为 .
三、解答题(共66分)
17.(6分)如图,在矩形ABCD中,点E在BE上,AE=AD,DF⊥AE,垂足为F.
求证:DF=AB.
第17题图 第18题图 第19题图 第20题图
18.(8分)如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,AE∥CD,CE∥AB,判断四边形ADCE的形状,并证明你的结论.
19.(8分)如图,点P是正方形ABCD的对角线AC上的一点,PM⊥AB,PN⊥BC,垂足分别为M,N,求证:DP=MN.
20.(10分)如图,在ABCD中,过点D作DE⊥AB于点E,点F在边CD上,BE=DF,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
21.(10分)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=,BD=2,求OE的长.
第21题图
22.(12分)如图,已知正方形ABCD的边长为,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
(1)求DE的长;
(2)过点E作EF⊥CE,交AB于点F,求BF的长;
第22题图
23.(12分)如图22,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为等边三角形,点E,F分别在菱形的边BC,CD上滑动,且E,F不与点B,C,D重合.
(1)求证:BE=CF;
(2)当点E,F在BC,CD上滑动时,四边形AECF的面积是否发生变化?如果不变,说明理由并求值.
第23题图
附加题(20分,不计入总分)
24. 如图①,在矩形纸片ABCD中,AB=3 cm,AD=5 cm,折叠纸片使点B落在边AD上的点E处,折痕为PQ,过点E作EF∥AB交PQ于点F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P,Q也随之移动.
①当点Q与点C重合时(如图②),求菱形BFEP的边长;
②若限定点P,Q分别在边BA,BC上移动,求点E在边AD上移动的最大距离.
第24题图
参考答案
一、1.C 2.A 3.C 4.B 5.C 6.A 7.D 8.B 9.D 10.C
二、11.1 12.4 13.4 14.13 15.2+2 16.或
三、17.证明:因为四边形ABCD是矩形,所以AD∥BC,∠B=90°.所以∠AEB=∠DAF.
又因为DF⊥AE,所以∠DFA=90°.所以∠DFA=∠B.
在△ADF和△EAB中,∠DFA=∠B,∠DAF=∠AEB,AD=AE,所以△ADF≌△EAB.
所以DF=AB.
18.解:四边形ADCE是菱形.
证明:为AE∥CD,CE∥AB,所以四边形ADCE是平行四边形.
又因为在Rt△ABC中,∠ACB=90°,D是AB的中点,所以CD=AD.
所以四边形ADCE是菱形.
19.证明:连结PB.
因为四边形ABCD是正方形,所以BC=DC,∠BCP=∠DCP=45°.
在△CBP和△CDP中,BC=DC,∠BCP=∠DCP,PC=PC,所以△CBP≌△CDP.所以DP=BP.
因为PM⊥AB,PN⊥BC,∠MBN=90°,所以四边形BNPM是矩形.所以BP=MN.
所以DP=MN.
20.证明:(1)因为四边形ABCD是平行四边形,所以BE∥DF.又因为BE=DF,所以四边形BFDE是平行四边形.因为DE⊥AB,所以∠DEB=90°.所以四边形BFDE是矩形.
(2)因为四边形ABCD是平行四边形,所以AD=BC,AB∥DC.所以∠DFA=∠FAB.
由(1)可知四边形BFDE是矩形,所以∠BFD=90°.所以∠BFC=90°.
在Rt△BCF中,由勾股定理,得BC=5.所以AD=BC=5.因为DF=5,所以AD=DF.
所以∠DAF=∠DFA.所以∠DAF=∠FAB,即AF平分∠DAB.
21.解:(1)因为AB∥DC,所以∠CAB=∠ACD.
因为AC平分∠BAD,所以∠CAB=∠CAD.所以∠CAD=∠ACD.所以AD=CD.
因为AB=AD,所以AB=CD.因为AB∥DC,所以四边形ABCD是平行四边形.
因为AB=AD,所以ABCD是菱形.
(2)因为四边形ABCD是菱形,所以AC⊥BD,OA=OC=AC,OB=OD=BD=1.
在Rt△AOB中,OA==2.
因为CE⊥AB,所以∠AEC=90°.
在Rt△AEC中,O为AC的中点,所以OE=AC=OA=2.
22.解:(1)因为四边形ABCD是正方形,所以∠ABC=∠ADC=90°,∠DBC=∠BCA=∠ACD=45°.
因为CE平分∠ACD,所以∠ACE=∠DCE=∠ACD=22.5°.
所以∠BCE=∠BCA+∠ACE=45°+22.5°=67.5°.
因为∠DBC=45°,所以∠BEC=180°﹣67.5°﹣45°=67.5°=∠BCE.所以BE=BC=.
在Rt△ACD中,由勾股定理,得BD==2.
所以DE=BD﹣BE=2﹣.
(2)因为EF⊥CE,所以∠CEF=90°.所以∠FEB=∠CEF﹣∠CEB=90°﹣67.5°=22.5°=∠DCE.
因为∠FBE=∠CDE=45°,BE=BC=CD,所以△FEB≌△ECD.所以BF=DE=2﹣.
23.(1)证明:因为四边形ABCD是菱形,∠BAD=120°,所以∠B=60°,∠BAC=
∠BAD=60°.
所以△ABC为等边三角形,则AB=BC=AC.因为△AEF为等边三角形,所以AE=AF,∠EAF=60°.
所以∠BAC-∠EAC=∠EAF-∠EAC,即∠BAE=∠CAF.所以△BAE≌△CAF.所以BE=CF.
(2)解:四边形AECF的面积不会发生变化.
理由:因为△BAE≌△CAF,所以S△ABE=S△ACF.所以S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC.
因为△ABC的面积是定值,所以四边形AECF的面积不会发生变化.
连接BD交AC于点O.在Rt△ABO中,AB=4,AO=2,由勾股定理,得BO=2.
S△ABC=×4×2=4,即四边形AECF的面积是4.
24.(1)证明:由折叠可得BP=EP,∠BPF=∠EPF.
又因为PF=PF,所以△PBF≌△PEF.所以BF=EF.
因为EF∥AB,所以∠BPF=∠EFP.所以∠EPF=∠EFP.所以EP=EF.
所以BP=BF=EF=EP.所以四边形BFEP为菱形.
(2)解:①因为四边形ABCD是矩形,所以BC=AD=5 cm,CD=AB=3 cm,∠A=∠D=90°.
由折叠可得BP=EP,CE=BC=5 cm.
在Rt△CDE中,由勾股定理,得DE=4 cm.所以AE=AD-DE=5-4=1(cm).
设BP=EP=x cm,则AP=(3-x)cm.
在Rt△APE中,由勾股定理,得EP2=AE2+AP2,即x2=12+(3-x)2,解得x=.
所以菱形BFEP的边长为cm.
②当点Q与点C重合时,点E离点A最近,由①知,此时AE=1 cm.
当点P与点A重合时,点E离点A最远,此时四边形ABQE为正方形,AE=AB=3 cm.
3-1=2(cm),所以点E在边AD上移动的最大距离为2 cm.
A
B
E
D
C
O
PAGE
5
1、选择题(每小题3分,共30分)
1.下列说法不正确的是( )
A.对角线互相垂直的矩形是正方形 B.对角线相等的菱形是正方形
C.有一个角是直角的平行四边形是正方形 D.邻边相等的矩形是正方形
2.如图,把一张矩形纸片ABCD沿EF折叠后,点C,D分别落在C′,D′的位置上,EC′交AD于点G.若∠EFG=58°,则∠FEG的度数是( )
A. 58° B. 60° C. 45° D. 30°
第2题图 第3题图 第4题图 第5题图
3.如图,把一张矩形纸片对折两次,然后剪下一个角并打开,剪出的纸片形状一定是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
4.如图,在Rt△ABC中,CD是斜边AB上的中线,若∠A=20°,则∠BDC的度数为( )
A.30° B.40° C.45° D.60°
5.如图,菱形ABCD的周长是20,对角线AC,BD相交于点O,若BD=6,则菱形ABCD的面积是( )
A.6 B.12 C.24 D.48
第第6题图 第7题图 第8题图 第9题图
6.如图,过正方形ABCD的顶点B作直线l,过A,C作直线l的垂线,垂足分别为E,F,若AE=1,CF=3,则AB的长为( )
A. B.10 C.3 D.
7.如图,在△ABC中,D是BC边上的点(与 B,C两点不重合),过点D 作DE∥AC,DF∥AB, 分别交 AB,AC于 E,F 两点,下列说法正确的是( )
A. 若 AD⊥BC,则四边形 AEDF 是矩形 B. 若 AD垂直平分 BC,则四边形AEDF 是矩形
C. 若 BD=CD,则四边形 AEDF 是菱形 D. 若 AD 平分 ∠BAC,则四边形AEDF是菱形
8.如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
A.10 B.12 C.18 D.24
9.如图,在正方形ABCD的外侧作等边三角形ADE,连接BE交AD于点F,则∠DFE的度数为( )
A. 45° B. 55° C. 60° D. 75°
10.如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于E,点G是AE中点且∠AOG=30°,则下列结论:①DC=3OG;②OG=BC;③△OGE是等边三角形;④S△AOE=S矩形ABCD.其中正确的个数为( )
A.1 B.2 C.3 D.4 第10题图
2、填空题(每小题4分,共24分)
11.已知正方形ABCD的对角线AC=,则正方形ABCD的面积为___________.
12.在矩形ABCD中,对角线AC,BD相交于点O,若∠AOB=60°,AB=4 cm,则BC的长为____cm.
第13题图 第14题图 第15题图 第16题图
13.如图,在∠MON的两边上分别截取OA,OB,使OA=OB;分别以点A,B为圆心,OA的长为半径画弧,两弧交于点C;连接AC,BC,AB,OC.若AB=2 cm,四边形OACB的面积为4 cm2,则OC的长为________cm.
14.如图,在△ABC 中,CD⊥AB交AB于点D,BE⊥AC交AC于点E,F为BC 的中点,DE=5,BC=8,则△DEF的周长是 .
15.如图,菱形ABCD中,∠ABC=120°,AB=4,E是BC边的中点,点P在对角线AC上,连接BP,EP,则△BPE周长的最小值为___________.
16.如图,在矩形ABCD中,AD=5,AB=8,点 E为 DC边上的一个动点,把 沿 折叠,当点D的对应点刚好落在矩形ABCD 的对称轴上时,则DE的长为 .
三、解答题(共66分)
17.(6分)如图,在矩形ABCD中,点E在BE上,AE=AD,DF⊥AE,垂足为F.
求证:DF=AB.
第17题图 第18题图 第19题图 第20题图
18.(8分)如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,AE∥CD,CE∥AB,判断四边形ADCE的形状,并证明你的结论.
19.(8分)如图,点P是正方形ABCD的对角线AC上的一点,PM⊥AB,PN⊥BC,垂足分别为M,N,求证:DP=MN.
20.(10分)如图,在ABCD中,过点D作DE⊥AB于点E,点F在边CD上,BE=DF,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
21.(10分)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=,BD=2,求OE的长.
第21题图
22.(12分)如图,已知正方形ABCD的边长为,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
(1)求DE的长;
(2)过点E作EF⊥CE,交AB于点F,求BF的长;
第22题图
23.(12分)如图22,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为等边三角形,点E,F分别在菱形的边BC,CD上滑动,且E,F不与点B,C,D重合.
(1)求证:BE=CF;
(2)当点E,F在BC,CD上滑动时,四边形AECF的面积是否发生变化?如果不变,说明理由并求值.
第23题图
附加题(20分,不计入总分)
24. 如图①,在矩形纸片ABCD中,AB=3 cm,AD=5 cm,折叠纸片使点B落在边AD上的点E处,折痕为PQ,过点E作EF∥AB交PQ于点F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P,Q也随之移动.
①当点Q与点C重合时(如图②),求菱形BFEP的边长;
②若限定点P,Q分别在边BA,BC上移动,求点E在边AD上移动的最大距离.
第24题图
参考答案
一、1.C 2.A 3.C 4.B 5.C 6.A 7.D 8.B 9.D 10.C
二、11.1 12.4 13.4 14.13 15.2+2 16.或
三、17.证明:因为四边形ABCD是矩形,所以AD∥BC,∠B=90°.所以∠AEB=∠DAF.
又因为DF⊥AE,所以∠DFA=90°.所以∠DFA=∠B.
在△ADF和△EAB中,∠DFA=∠B,∠DAF=∠AEB,AD=AE,所以△ADF≌△EAB.
所以DF=AB.
18.解:四边形ADCE是菱形.
证明:为AE∥CD,CE∥AB,所以四边形ADCE是平行四边形.
又因为在Rt△ABC中,∠ACB=90°,D是AB的中点,所以CD=AD.
所以四边形ADCE是菱形.
19.证明:连结PB.
因为四边形ABCD是正方形,所以BC=DC,∠BCP=∠DCP=45°.
在△CBP和△CDP中,BC=DC,∠BCP=∠DCP,PC=PC,所以△CBP≌△CDP.所以DP=BP.
因为PM⊥AB,PN⊥BC,∠MBN=90°,所以四边形BNPM是矩形.所以BP=MN.
所以DP=MN.
20.证明:(1)因为四边形ABCD是平行四边形,所以BE∥DF.又因为BE=DF,所以四边形BFDE是平行四边形.因为DE⊥AB,所以∠DEB=90°.所以四边形BFDE是矩形.
(2)因为四边形ABCD是平行四边形,所以AD=BC,AB∥DC.所以∠DFA=∠FAB.
由(1)可知四边形BFDE是矩形,所以∠BFD=90°.所以∠BFC=90°.
在Rt△BCF中,由勾股定理,得BC=5.所以AD=BC=5.因为DF=5,所以AD=DF.
所以∠DAF=∠DFA.所以∠DAF=∠FAB,即AF平分∠DAB.
21.解:(1)因为AB∥DC,所以∠CAB=∠ACD.
因为AC平分∠BAD,所以∠CAB=∠CAD.所以∠CAD=∠ACD.所以AD=CD.
因为AB=AD,所以AB=CD.因为AB∥DC,所以四边形ABCD是平行四边形.
因为AB=AD,所以ABCD是菱形.
(2)因为四边形ABCD是菱形,所以AC⊥BD,OA=OC=AC,OB=OD=BD=1.
在Rt△AOB中,OA==2.
因为CE⊥AB,所以∠AEC=90°.
在Rt△AEC中,O为AC的中点,所以OE=AC=OA=2.
22.解:(1)因为四边形ABCD是正方形,所以∠ABC=∠ADC=90°,∠DBC=∠BCA=∠ACD=45°.
因为CE平分∠ACD,所以∠ACE=∠DCE=∠ACD=22.5°.
所以∠BCE=∠BCA+∠ACE=45°+22.5°=67.5°.
因为∠DBC=45°,所以∠BEC=180°﹣67.5°﹣45°=67.5°=∠BCE.所以BE=BC=.
在Rt△ACD中,由勾股定理,得BD==2.
所以DE=BD﹣BE=2﹣.
(2)因为EF⊥CE,所以∠CEF=90°.所以∠FEB=∠CEF﹣∠CEB=90°﹣67.5°=22.5°=∠DCE.
因为∠FBE=∠CDE=45°,BE=BC=CD,所以△FEB≌△ECD.所以BF=DE=2﹣.
23.(1)证明:因为四边形ABCD是菱形,∠BAD=120°,所以∠B=60°,∠BAC=
∠BAD=60°.
所以△ABC为等边三角形,则AB=BC=AC.因为△AEF为等边三角形,所以AE=AF,∠EAF=60°.
所以∠BAC-∠EAC=∠EAF-∠EAC,即∠BAE=∠CAF.所以△BAE≌△CAF.所以BE=CF.
(2)解:四边形AECF的面积不会发生变化.
理由:因为△BAE≌△CAF,所以S△ABE=S△ACF.所以S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC.
因为△ABC的面积是定值,所以四边形AECF的面积不会发生变化.
连接BD交AC于点O.在Rt△ABO中,AB=4,AO=2,由勾股定理,得BO=2.
S△ABC=×4×2=4,即四边形AECF的面积是4.
24.(1)证明:由折叠可得BP=EP,∠BPF=∠EPF.
又因为PF=PF,所以△PBF≌△PEF.所以BF=EF.
因为EF∥AB,所以∠BPF=∠EFP.所以∠EPF=∠EFP.所以EP=EF.
所以BP=BF=EF=EP.所以四边形BFEP为菱形.
(2)解:①因为四边形ABCD是矩形,所以BC=AD=5 cm,CD=AB=3 cm,∠A=∠D=90°.
由折叠可得BP=EP,CE=BC=5 cm.
在Rt△CDE中,由勾股定理,得DE=4 cm.所以AE=AD-DE=5-4=1(cm).
设BP=EP=x cm,则AP=(3-x)cm.
在Rt△APE中,由勾股定理,得EP2=AE2+AP2,即x2=12+(3-x)2,解得x=.
所以菱形BFEP的边长为cm.
②当点Q与点C重合时,点E离点A最近,由①知,此时AE=1 cm.
当点P与点A重合时,点E离点A最远,此时四边形ABQE为正方形,AE=AB=3 cm.
3-1=2(cm),所以点E在边AD上移动的最大距离为2 cm.
A
B
E
D
C
O
PAGE
5
