鲁教版八年级数学下册第六章 特殊平行四边形测试题(含答案)
文档属性
| 名称 | 鲁教版八年级数学下册第六章 特殊平行四边形测试题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 166.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-06 00:00:00 | ||
图片预览

文档简介
第六章 特殊平行四边形测试题
一、选择题(每小题3分,共30分)
1.已知下列命题:①矩形是轴对称图形,且有两条对称轴;②两条对角线相等的四边形是矩形;③有两个角相等的平行四边形是矩形;④两条对角线相等且互相平分的四边形是矩形.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
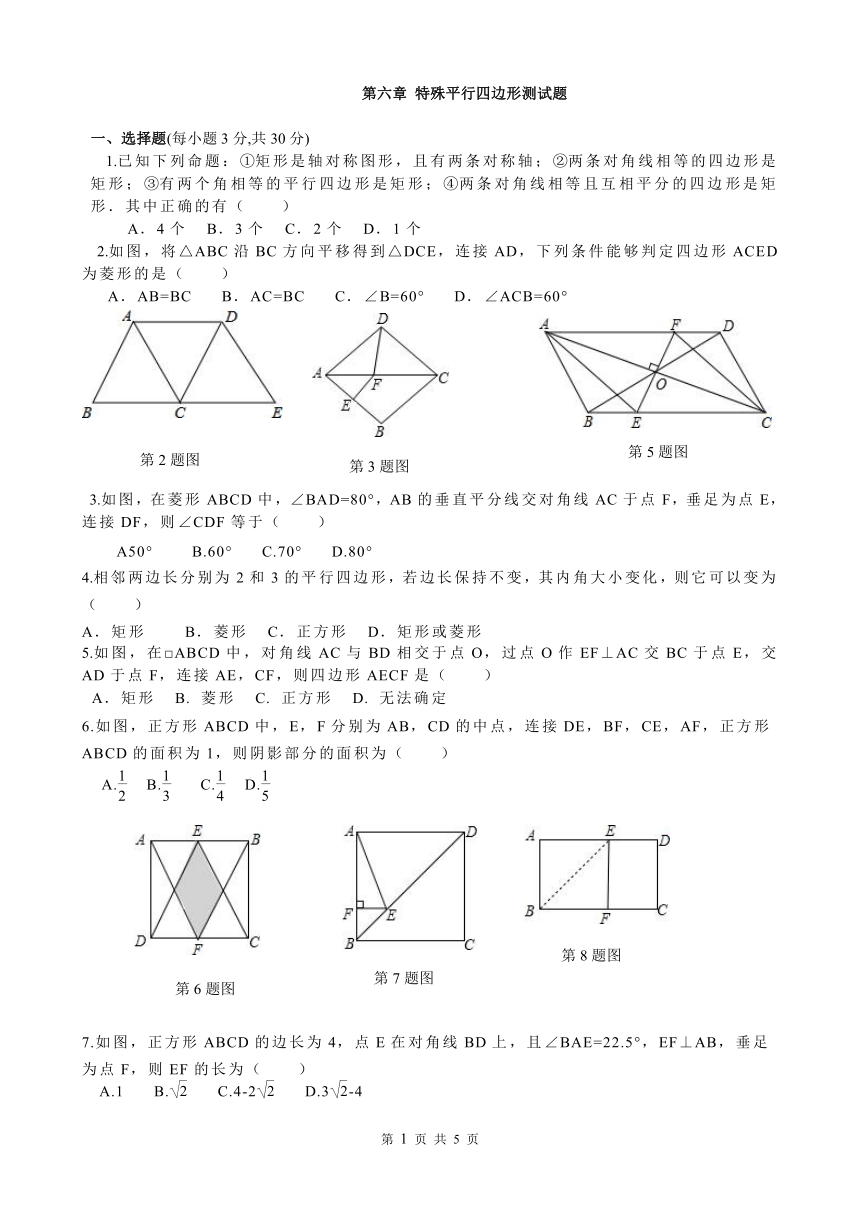
2.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( )
A.AB=BC B.AC=BC C.∠B=60° D.∠ACB=60°
3.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为点E,连接DF,则∠CDF等于( )
A50° B.60° C.70° D.80°
4.相邻两边长分别为2和3的平行四边形,若边长保持不变,其内角大小变化,则它可以变为( )
A.矩形 B.菱形 C.正方形 D.矩形或菱形
5.如图,在□ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE,CF,则四边形AECF是( )
A.矩形 B. 菱形 C. 正方形 D. 无法确定
6.如图,正方形ABCD中,E,F分别为AB,CD的中点,连接DE,BF,CE,AF,正方形ABCD的面积为1,则阴影部分的面积为( )
A. B. C. D.
7.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF的长为( )
A.1 B. C.4-2 D.3-4
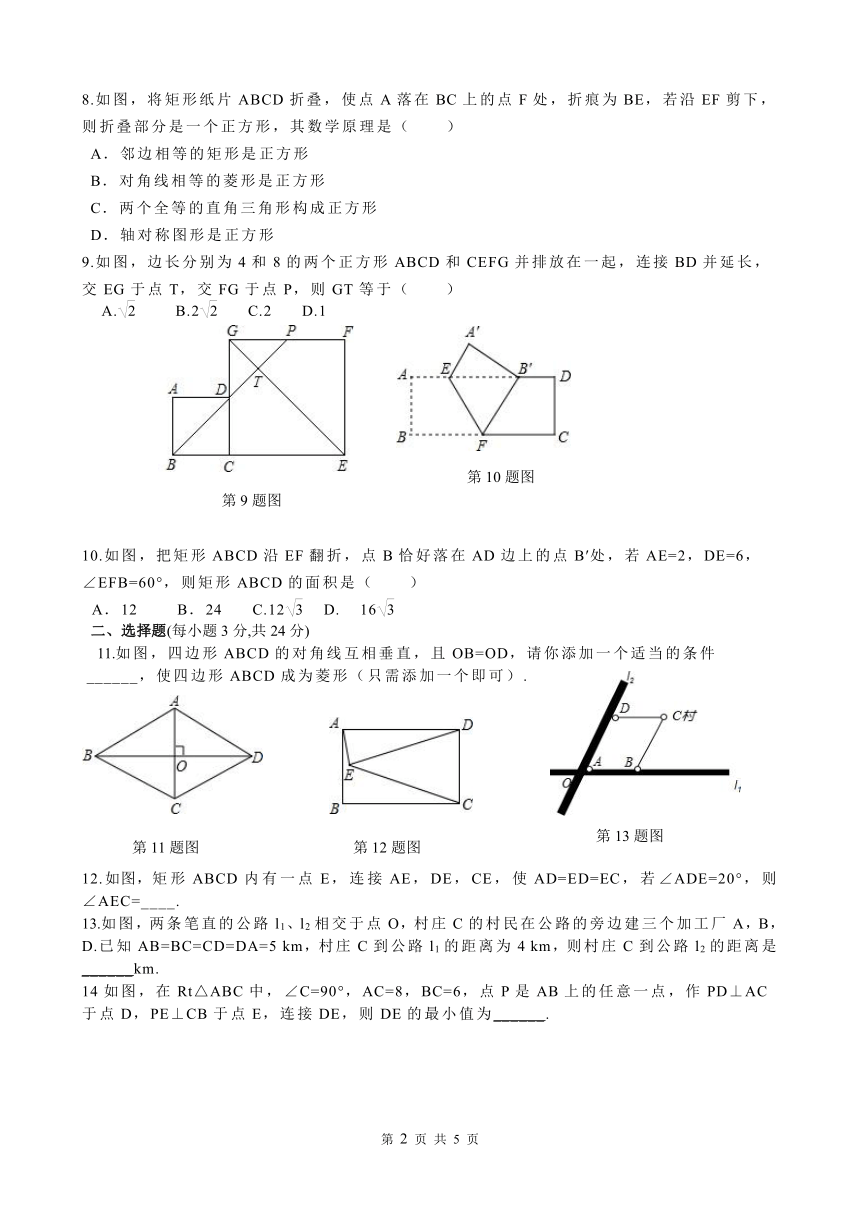
8.如图,将矩形纸片ABCD折叠,使点A落在BC上的点F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( )
A.邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形
D.轴对称图形是正方形
9.如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长,交EG于点T,交FG于点P,则GT等于( )
A. B.2 C.2 D.1
10.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边上的点B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
A.12 B.24 C.12 D. 16
二、选择题(每小题3分,共24分)
11.如图,四边形ABCD的对角线互相垂直,且OB=OD,请你添加一个适当的条件
?______,使四边形ABCD成为菱形(只需添加一个即可).
12.如图,矩形ABCD内有一点E,连接AE,DE,CE,使AD=ED=EC,若∠ADE=20°,则∠AEC=____.
13.如图,两条笔直的公路l1、l2相交于点O,村庄C的村民在公路的旁边建三个加工厂A,B,D.已知AB=BC=CD=DA=5 km,村庄C到公路l1的距离为4 km,则村庄C到公路l2的距离是______km.
14如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P是AB上的任意一点,作PD⊥AC于点D,PE⊥CB于点E,连接DE,则DE的最小值为______.
15.如图,已知四边形ABCD是菱形,∠A=72°,将它分割成如图所示的四个等腰三角形,那么∠1+∠2+∠3=______度.
16.如图,一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α为______度时,两条对角线长度相等.
17.如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.若点O运动到AC的中点,则∠ACB=_____°时,四边形AECF是正方形.
18.如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连接AD1,BC1.若∠ACB=30°,AB=1,CC1=x,则下列结论:①△A1AD1≌△CC1B;②当x=1时,四边形ABC1D1是菱形;③当x=2时,△BDD1为等边三角形.其中正确的是 (填序号).
三 、解答题 (共66分)
19.(6分)如图,在四边形ABCD中,∠ABC=∠ADC=90°,点P是AC的中点.求证:∠BDP=∠DBP.
20.(6分)如图,在直线MN上和直线MN外分别取点A,B,过线段AB的中点作CD∥MN,分别与∠MAB与∠NAB的平分线相交于点C,D.求证:四边形ACBD是矩形.
21.(8分)如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.
(1)求证:AE=EC;
(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC上的什么位置?说明理由.
22.(8分)如图,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,垂足分别是点E,F,并且DE=DF.
求证:(1)△ADE≌△CDF;
(2)四边形ABCD是菱形.
23.(8分)如图,Rt△ABE与Rt△DCF关于直线m对称,已知∠B=90°,∠C=90°,连接EF,AD,点B,E,F,C在同一条直线上.求证:四边形ABCD是矩形.
第23题图 第24题图
24.(8分)如图, 在△ACD中,∠ADC=90°,∠ADC的平分线交AC于点E,EF⊥AD交AD于点F,EG⊥DC交DC于点G,请你说明四边形EFDG是正方形.
25.(10分)如图,正方形ABCD中,动点E在AC上,AF⊥AC,且AF=AE.
(1)求证:BF=DE;
(2)当点E运动到AC的中点时(其他条件都保持不变),四边形AFBE是什么特殊四边形?说明理由.
26.(12分)如图,矩形ABCD中,对角线AC,BD相交于O点,点P是线段AD上一动点(不与点D重合),PO的延长线交BC于Q点.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=3cm,AD=4cm,P从点A出发.以1cm/s的速度向点D匀速运动.设点P的运动时间为ts,问:四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
参考答案:
一、 1.C 2.B 3.B 4.A 5.B 6.C 7.C 8.A 9.B 10.D
二、11. 不唯一,如OA=OC 12. 120° 13.4 14. 4.8 15.90 16.90 17.90 18.①②③
三、19.证明:∵∠ABC=∠ADC=90°,P是AC的中点,∴BP=AC,PD=AC.
∴BP=PD.∴∠BDP=∠DBP.
20.证明:∵AD平分∠BAN,∴∠DAN=∠BAD.
∵CD∥MN,∴∠CDA=∠DAN.∴∠BAD=∠CDA.∴OD=OA.同理CO=OA.
∴CO=OD.∵AO=BO,∴四边形ACBD是平行四边形.
∵AC,AD均为角平分线,∴∠CAD=90°,∴四边形ACBD是矩形.
21. (1)提示:证△ADE≌△CDE即可.
(2)解:点F是线段BC的中点.
理由:连接AC.在菱形ABCD中,AB=BC.
又∵∠ABC=60°,∴△ABC是等边三角形.∴∠BAC=60°.
∵AE=EC,∠CEF=60°,∴∠EAC=∠BAC=30°.∴AF是△ABC的角平分线.
∴点F是线段BC的中点.
22.证明:(1)∵DE⊥AB,DF⊥BC,∴∠AED=∠CFD=90°.
∵四边形ABCD是平行四边形,∴∠A=∠C.
又DE=DF,∴△AED≌△CFD.
(2)∵△AED≌△CFD,∴AD=CD.∵四边形ABCD是平行四边形,∴四边形ABCD是菱形.
23.解:∵Rt△ABE与Rt△DCF关于直线m对称,∴AB=DC.
∵∠B=90°,∠C=90°,点B,E,F,C在同一条直线上,∴AB∥CD.
∴四边形ABCD是平行四边形.
∵∠B=90°,∴平行四边形ABCD是矩形.
24.解:∵∠ADC=90°,EF⊥AD,EG⊥CD,∴四边形EFDG是矩形.
又∵DE平分∠ADE,∴EF=EG.
∴四边形EFDG是菱形.∴四边形EFDG是正方形
25.(1)提示:由SAS证△ABF≌△ADE即可得BF=DE.
(2)解:当点E运动到AC的中点时,四边形AFBE是正方形.
理由:∵点E运动到AC的中点,AB=BC,∴BE⊥AC,BE=AE=AC.
∵AF=AE,∴BE=AF=AE.
又∠FAE=90°,∴BE∥AF.
∴四边形AFBE是平行四边形.∵∠FAE=90°,AF=AE,∴四边形AFBE是正方形.
26. (1)证明:∵四边形ABCD是矩形,∴AD∥BC,OD=OB.
∴∠PDO=∠QBO.
又∠POD=∠QOB,∴△POD≌△QOB.∴OP=OQ.
∴四边形PBQD为平行四边形.
(2)解:能.点P从点A出发运动ts时,AP=tcm,PD=(4-t)cm.
当四边形PBQD是菱形时,PB=PD=(4-t)cm.
∵四边形ABCD是矩形,∴∠BAP=90°.
∴在Rt△ABP中,AP2+AB2=PB2,即t2+32=(4-t)2.解得t=.
∴点P的运动时间为s时,四边形PBQD能够成为菱形.
第5题图
第3题图
第2题图
第8题图
第7题图
第6题图
第9题图
第10题图
第13题图
第11题图
第12题图
第16题图
第15题图
第14题图
第18题图
第17题图
第20题图
第19题图
第21题图
第22题图
第26题图
第25题图
一、选择题(每小题3分,共30分)
1.已知下列命题:①矩形是轴对称图形,且有两条对称轴;②两条对角线相等的四边形是矩形;③有两个角相等的平行四边形是矩形;④两条对角线相等且互相平分的四边形是矩形.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
2.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( )
A.AB=BC B.AC=BC C.∠B=60° D.∠ACB=60°
3.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为点E,连接DF,则∠CDF等于( )
A50° B.60° C.70° D.80°
4.相邻两边长分别为2和3的平行四边形,若边长保持不变,其内角大小变化,则它可以变为( )
A.矩形 B.菱形 C.正方形 D.矩形或菱形
5.如图,在□ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE,CF,则四边形AECF是( )
A.矩形 B. 菱形 C. 正方形 D. 无法确定
6.如图,正方形ABCD中,E,F分别为AB,CD的中点,连接DE,BF,CE,AF,正方形ABCD的面积为1,则阴影部分的面积为( )
A. B. C. D.
7.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF的长为( )
A.1 B. C.4-2 D.3-4
8.如图,将矩形纸片ABCD折叠,使点A落在BC上的点F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( )
A.邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形
D.轴对称图形是正方形
9.如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长,交EG于点T,交FG于点P,则GT等于( )
A. B.2 C.2 D.1
10.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边上的点B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
A.12 B.24 C.12 D. 16
二、选择题(每小题3分,共24分)
11.如图,四边形ABCD的对角线互相垂直,且OB=OD,请你添加一个适当的条件
?______,使四边形ABCD成为菱形(只需添加一个即可).
12.如图,矩形ABCD内有一点E,连接AE,DE,CE,使AD=ED=EC,若∠ADE=20°,则∠AEC=____.
13.如图,两条笔直的公路l1、l2相交于点O,村庄C的村民在公路的旁边建三个加工厂A,B,D.已知AB=BC=CD=DA=5 km,村庄C到公路l1的距离为4 km,则村庄C到公路l2的距离是______km.
14如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P是AB上的任意一点,作PD⊥AC于点D,PE⊥CB于点E,连接DE,则DE的最小值为______.
15.如图,已知四边形ABCD是菱形,∠A=72°,将它分割成如图所示的四个等腰三角形,那么∠1+∠2+∠3=______度.
16.如图,一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α为______度时,两条对角线长度相等.
17.如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.若点O运动到AC的中点,则∠ACB=_____°时,四边形AECF是正方形.
18.如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连接AD1,BC1.若∠ACB=30°,AB=1,CC1=x,则下列结论:①△A1AD1≌△CC1B;②当x=1时,四边形ABC1D1是菱形;③当x=2时,△BDD1为等边三角形.其中正确的是 (填序号).
三 、解答题 (共66分)
19.(6分)如图,在四边形ABCD中,∠ABC=∠ADC=90°,点P是AC的中点.求证:∠BDP=∠DBP.
20.(6分)如图,在直线MN上和直线MN外分别取点A,B,过线段AB的中点作CD∥MN,分别与∠MAB与∠NAB的平分线相交于点C,D.求证:四边形ACBD是矩形.
21.(8分)如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.
(1)求证:AE=EC;
(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC上的什么位置?说明理由.
22.(8分)如图,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,垂足分别是点E,F,并且DE=DF.
求证:(1)△ADE≌△CDF;
(2)四边形ABCD是菱形.
23.(8分)如图,Rt△ABE与Rt△DCF关于直线m对称,已知∠B=90°,∠C=90°,连接EF,AD,点B,E,F,C在同一条直线上.求证:四边形ABCD是矩形.
第23题图 第24题图
24.(8分)如图, 在△ACD中,∠ADC=90°,∠ADC的平分线交AC于点E,EF⊥AD交AD于点F,EG⊥DC交DC于点G,请你说明四边形EFDG是正方形.
25.(10分)如图,正方形ABCD中,动点E在AC上,AF⊥AC,且AF=AE.
(1)求证:BF=DE;
(2)当点E运动到AC的中点时(其他条件都保持不变),四边形AFBE是什么特殊四边形?说明理由.
26.(12分)如图,矩形ABCD中,对角线AC,BD相交于O点,点P是线段AD上一动点(不与点D重合),PO的延长线交BC于Q点.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=3cm,AD=4cm,P从点A出发.以1cm/s的速度向点D匀速运动.设点P的运动时间为ts,问:四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
参考答案:
一、 1.C 2.B 3.B 4.A 5.B 6.C 7.C 8.A 9.B 10.D
二、11. 不唯一,如OA=OC 12. 120° 13.4 14. 4.8 15.90 16.90 17.90 18.①②③
三、19.证明:∵∠ABC=∠ADC=90°,P是AC的中点,∴BP=AC,PD=AC.
∴BP=PD.∴∠BDP=∠DBP.
20.证明:∵AD平分∠BAN,∴∠DAN=∠BAD.
∵CD∥MN,∴∠CDA=∠DAN.∴∠BAD=∠CDA.∴OD=OA.同理CO=OA.
∴CO=OD.∵AO=BO,∴四边形ACBD是平行四边形.
∵AC,AD均为角平分线,∴∠CAD=90°,∴四边形ACBD是矩形.
21. (1)提示:证△ADE≌△CDE即可.
(2)解:点F是线段BC的中点.
理由:连接AC.在菱形ABCD中,AB=BC.
又∵∠ABC=60°,∴△ABC是等边三角形.∴∠BAC=60°.
∵AE=EC,∠CEF=60°,∴∠EAC=∠BAC=30°.∴AF是△ABC的角平分线.
∴点F是线段BC的中点.
22.证明:(1)∵DE⊥AB,DF⊥BC,∴∠AED=∠CFD=90°.
∵四边形ABCD是平行四边形,∴∠A=∠C.
又DE=DF,∴△AED≌△CFD.
(2)∵△AED≌△CFD,∴AD=CD.∵四边形ABCD是平行四边形,∴四边形ABCD是菱形.
23.解:∵Rt△ABE与Rt△DCF关于直线m对称,∴AB=DC.
∵∠B=90°,∠C=90°,点B,E,F,C在同一条直线上,∴AB∥CD.
∴四边形ABCD是平行四边形.
∵∠B=90°,∴平行四边形ABCD是矩形.
24.解:∵∠ADC=90°,EF⊥AD,EG⊥CD,∴四边形EFDG是矩形.
又∵DE平分∠ADE,∴EF=EG.
∴四边形EFDG是菱形.∴四边形EFDG是正方形
25.(1)提示:由SAS证△ABF≌△ADE即可得BF=DE.
(2)解:当点E运动到AC的中点时,四边形AFBE是正方形.
理由:∵点E运动到AC的中点,AB=BC,∴BE⊥AC,BE=AE=AC.
∵AF=AE,∴BE=AF=AE.
又∠FAE=90°,∴BE∥AF.
∴四边形AFBE是平行四边形.∵∠FAE=90°,AF=AE,∴四边形AFBE是正方形.
26. (1)证明:∵四边形ABCD是矩形,∴AD∥BC,OD=OB.
∴∠PDO=∠QBO.
又∠POD=∠QOB,∴△POD≌△QOB.∴OP=OQ.
∴四边形PBQD为平行四边形.
(2)解:能.点P从点A出发运动ts时,AP=tcm,PD=(4-t)cm.
当四边形PBQD是菱形时,PB=PD=(4-t)cm.
∵四边形ABCD是矩形,∴∠BAP=90°.
∴在Rt△ABP中,AP2+AB2=PB2,即t2+32=(4-t)2.解得t=.
∴点P的运动时间为s时,四边形PBQD能够成为菱形.
第5题图
第3题图
第2题图
第8题图
第7题图
第6题图
第9题图
第10题图
第13题图
第11题图
第12题图
第16题图
第15题图
第14题图
第18题图
第17题图
第20题图
第19题图
第21题图
第22题图
第26题图
第25题图
