高中物理人教版必修2课件:5.6 向心力(共40张PPT)
文档属性
| 名称 | 高中物理人教版必修2课件:5.6 向心力(共40张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-06 15:08:46 | ||
图片预览









文档简介
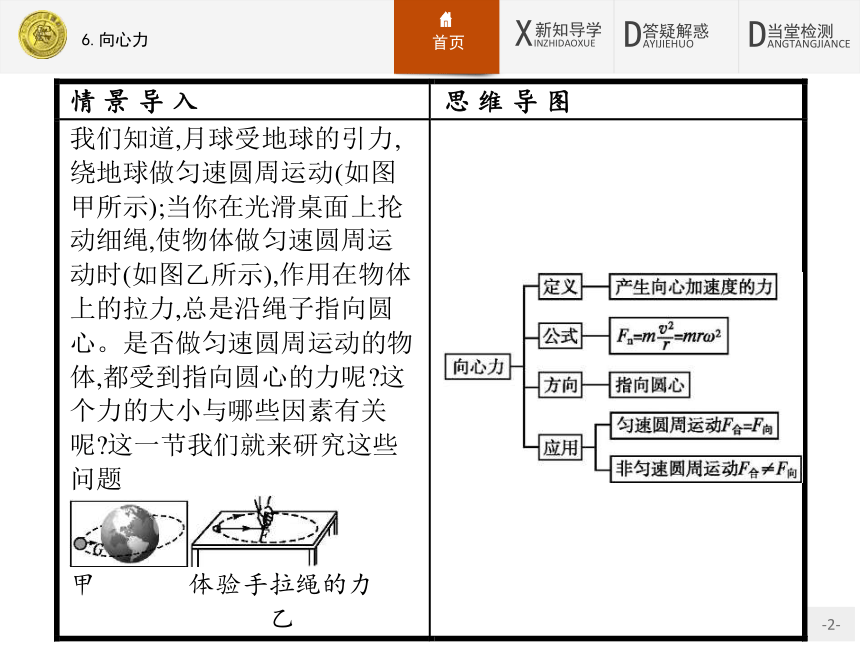
(共40张PPT)
6.向心力
填一填
练一练
一、向心力(见课本第23页)
1.定义:做匀速圆周运动的物体受到指向圆心的合力。
2.方向:始终指向圆心,与线速度方向垂直。
3.公式:Fn= 或Fn=mω2r。
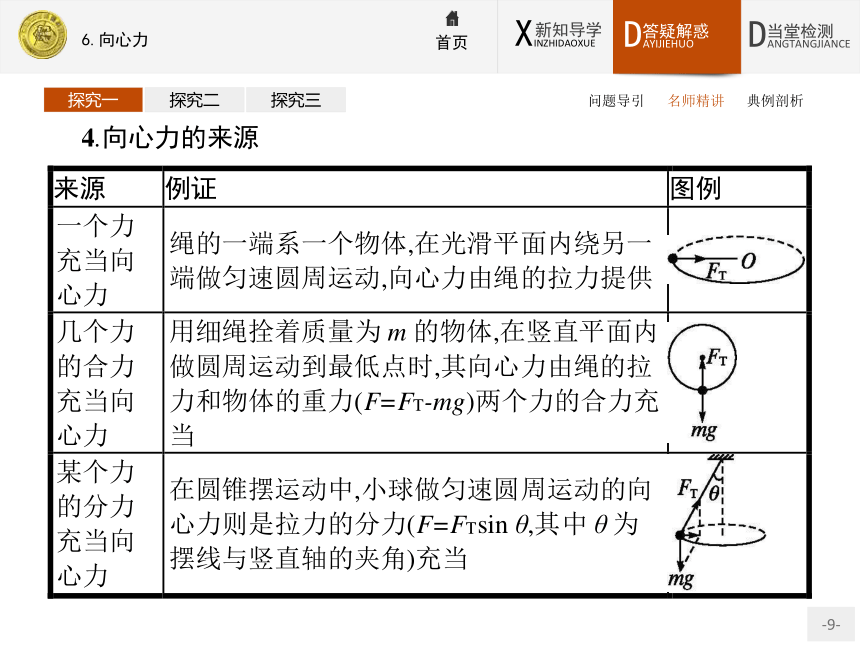
4.来源:
(1)向心力是按照力的作用效果命名的。
(2)匀速圆周运动中向心力可能是物体所受外力的合力,也可能是某个力的分力。
5.作用:产生向心加速度,改变线速度的方向。
填一填
练一练
二、变速圆周运动和一般的曲线运动(见课本第24页)
1.变速圆周运动
合力不指向圆心,合力F可以分解为互相垂直的两个分力。
(1)跟圆周相切的分力Ft产生切向加速度,切向加速度与物体的速度方向共线,它改变速度的大小。
(2)指向圆心的分力Fn产生向心加速度,与速度方向垂直,改变速度的方向。
填一填
练一练
2.一般的曲线运动的处理方法
(1)定义:运动轨迹既不是直线也不是圆周的曲线运动。
(2)处理方法:一般的曲线运动中,可以把曲线分割成许多很短的小段,每一小段可看作一小段圆弧,研究质点在这一小段的运动时,可以采用圆周运动的处理方法进行处理,如图所示。
填一填
练一练
在水平面上转弯的摩托车(如图),向心力的来源是( )
A.重力和支持力的合力 B.静摩擦力
C.滑动摩擦力 D.重力、支持力、牵引力的合力
解析:在水平面上转弯的摩托车,竖直方向受重力和地面的支持力,水平方向受地面给摩托车的静摩擦力,静摩擦力提供车辆转弯所需的向心力,而车轮没有相对路面打滑,故该摩擦力是静摩擦力。
答案:B
问题导引
名师精讲
典例剖析
探究一
探究二
探究三
向心力的大小、方向和来源?
汽车在水平路面上保持速度大小不变,请思考汽车转弯时的向心力是由什么力提供的。
问题导引
名师精讲
典例剖析
探究一
探究二
探究三
1.向心力的作用效果
改变线速度的方向。由于向心力始终指向圆心,其方向与物体运动方向始终垂直,故向心力不改变线速度的大小。
2.向心力的特点
①方向时刻在变化,总是与线速度的方向垂直。②在匀速圆周运动中,向心力大小不变,向心力是变力,是一个按效果命名的力。
3.向心力的大小
问题导引
名师精讲
典例剖析
探究一
探究二
探究三
4.向心力的来源
问题导引
名师精讲
典例剖析
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
探究一
探究二
探究三
【例题1】 (多选)如图所示,小物体m与圆盘保持相对静止,随盘一起做匀速圆周运动,则物体的受力情况是( )
A.受重力、支持力、静摩擦力和向心力的作用
B.摩擦力的方向始终指向圆心O
C.重力和支持力是一对平衡力
D.摩擦力是使物体做匀速圆周运动的向心力
解析:分析圆盘上小物体的受力情况。竖直方向,受到重力和支持力作用,处于平衡状态;水平方向,物体随圆盘做圆周运动,由摩擦力提供向心力,故摩擦力方向指向圆心,选项B、C、D正确。
答案:BCD
问题导引
名师精讲
典例剖析
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
探究一
探究二
探究三
变式训练1 导学号61270027有一个惊险的杂技节目叫“飞车走壁”,杂技演员骑摩托车先在如图所示的大型圆筒底部做速度较小、半径较小的圆周运动,通过逐步加速,圆周运动的半径逐步增大,最后能以较大的速度在竖直的壁上做匀速圆周运动,这时使车子和人整体做匀速圆周运动的向心力是 ( )
A.圆筒壁对车的静摩擦力
B.筒壁对车的弹力
C.摩托车本身的动力
D.重力和摩擦力的合力
问题导引
名师精讲
典例剖析
探究一
探究二
探究三
解析:在竖直的壁上的摩托车只受三个力作用,其中竖直方向上重力与摩擦力是一对平衡力,水平方向上筒壁对车的弹力提供了车子和人整体做匀速圆周运动的向心力,选项B正确。
答案:B
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
匀速圆周运动的特点及解题方法?
飞机在空中水平面内做匀速圆周运动,如图所示。试分析:
(1)飞机受到哪些力的作用?向心力有谁提供?
(2)若知道飞机做圆周运动的半径,如何求得飞机运动的速度大小?
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
1.匀速圆周运动的特点
线速度大小不变,方向时刻改变;角速度、周期、频率都恒定不变;向心加速度和向心力大小都恒定不变,但方向时刻改变。
2.匀速圆周运动的性质
(1)线速度仅大小不变而方向时刻改变,是变速运动。
(2)向心加速度仅大小恒定而方向时刻改变,是非匀变速曲线运动。
(3)匀速圆周运动具有周期性,即每经过一个周期物体都要重新回到原来的位置,其运动状态(如v、a大小及方向)也要重复原来的情况。
(4)做匀速圆周运动的物体所受外力的合力大小恒定,方向总是沿半径指向圆心。
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
3.匀速圆周运动问题的解题步骤
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
【例题2】导学号61270028如图所示,双人花样滑冰运动中男运动员拉着女运动员做圆锥摆运动的精彩场面,观众有时会看到女运动员被男运动员拉着离开冰面在空中做水平方向的匀速圆周运动。若女运动员做圆锥摆运动时和竖直方向的夹角约为θ,女运动员的质量为m,转动过程中女运动员的重心做匀速圆周运动的半径为r,求:
(1)男运动员对女运动员的拉力大小。
(2)男运动员转动的角速度。
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
点拨以女运动员为研究对象,受到重力和男运动员对她的拉力作用,这两个力的合力提供向心力,其做圆周运动的平面在水平面内。根据牛顿第二定律求解。
解析:设男运动员对女运动员的拉力大小为F,女运动员受力如图所示,
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
变式训练2 如图所示,质量为1 kg的小球用细绳悬挂于O点,将小球拉离竖直位置释放后,到达最低点时的速度为 2 m/s,已知球心到悬点的距离为1 m,重力加速度g取10 m/s2,求小球在最低点时对绳的拉力的大小。
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
解析:小球在最低点时做圆周运动的向心力由重力mg和绳的拉力FT提供(如图所示)
根据牛顿第二定律有
解得FT=14 N
由牛顿第三定律知,小球在最低点时对绳的拉力大小为14 N。
答案:14 N
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
4.圆周运动中的连接体问题
(1)圆周运动中的连接体问题处理方法:此类问题的处理方法与单个物体的情况基本相同。因系统内的每个物体的速度、加速度不同,即运动状态不同,所以处理时应隔离每个物体进行分析。若物体存在加速度,应根据牛顿第二定律列方程求解;若物体处于平衡状态,应结合平衡条件进行处理。
(2)圆周运动中的连接体问题的几种典型情景
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
【例题3】导学号61270029如图所示,OM=MN=R。两个小球质量都是m,a、b为水平轻绳。两小球正随水平圆盘以角速度ω匀速同步转动。小球和圆盘间的摩擦力可以不计。求:
(1)绳b对小球N的拉力大小。
(2)绳a对小球M的拉力大小。
点拨两球所受的重力和水平面的支持力在竖直面内,且是一对平衡力,不能提供向心力。M球所受到的向心力由绳a和绳b的拉力的合力提供,N球所受到的向心力由杆的绳b的拉力提供。
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
解析:(1)对球N,受力如图所示,
其做圆周运动的半径为2R,
根据牛顿第二定律有
Fb=mω2·2R=2mω2R。
(2)对球M,受力如图所示,
其做圆周运动的半径为R,
根据牛顿第二定律有
Fa-Fb'=mω2R
Fb=Fb'
解得Fa=Fb+mω2R=3mω2R。
答案:(1)2mω2R (2)3mω2R
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
变速圆周运动和一般曲线的运动?
如图所示,荡秋千是小朋友很喜欢的游戏,当秋千由上向下荡时,(1)此时小朋友做的是匀速圆周运动还是变速圆周运动?(2)绳子拉力与重力的合力指向悬挂点吗?
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
1.匀速圆周运动和变速圆周运动的区别
(1)由做曲线运动的条件可知,变速圆周运动中物体所受的合力与速度方向一定不垂直,当速率增大时,物体受到的合力与瞬时速度之间的夹角是锐角;当速率减小时,物体受到的合力与速度之间的夹角是钝角。
(2)匀速圆周运动和变速圆周运动受力情况的不同是:匀速圆周运动中,合力全部用来提供向心力,合力指向圆心;变速圆周运动中,合力沿着半径方向的分量提供向心力,合力通常不指向圆心。
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
2.一般的曲线运动
运动轨迹既不是直线也不是圆周的曲线运动,称为一般曲线运动,在复杂的曲线运动中取一小段研究,每一小段都可以看成是圆周的一部分,这些圆弧的弯曲程度不同,圆心不同,注意到这个区别以后,在分析质点经过曲线上某位置的运动时,就可以采用圆周运动的方法进行研究,如图所示。
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
【例题4】 一般的曲线运动可以分成很多小段,每小段都可以看成圆周运动的一部分,即把整条曲线用一系列不同半径的小圆弧来代替。如图甲所示,曲线上的A点的曲率圆定义为:通过A点和曲线上紧邻A点两侧的两点作一圆,在极限情况下,这个圆就叫作A点的曲率圆,其半径ρ叫作A点的曲率半径。现将一物体沿与水平面成α角的方向以速度v0抛出,如图乙所示。则在其轨迹最高点P处的曲率半径是( )
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
解析:根据运动的分解,物体在最高点的速度等于水平分速度,即为v0cos α,在最高点看成是向心力为重力的圆周运动的一部分,则
答案:C
1 2 3 4 5
1.(多选)关于向心力,下列说法正确的是( )
A.向心力是一种效果力
B.向心力是一种具有某种性质的力
C.向心力既可以改变速度的方向,又可以改变速度的大小
D.向心力只改变速度的方向,不改变速度的大小
解析:向心力是按作用效果命名的,是一种效果力,它可以由重力、弹力、摩擦力等性质的力提供,所以选项A正确,B错误;由于向心力始终沿半径指向圆心,与速度的方向垂直,即向心力不改变速度的大小,只改变速度的方向,因此选项C错误,D正确。
答案:AD
1 2 3 4 5
2.如图所示,将一质量为m的摆球用长为L的细绳吊起,上端固定,使摆球在水平面内做匀速圆周运动,细绳就会沿圆锥面旋转,这样就构成了一个圆锥摆。关于摆球的受力情况,下列说法中正确的是( )
A.摆球受重力、拉力和向心力的作用
B.摆球受拉力和向心力的作用
C.摆球受重力和拉力的作用
D.摆球受重力和向心力的作用
解析:物体只受重力G和拉力F的作用,而向心力是重力和拉力的合力。也可以认为向心力就是F沿水平方向的分力,显然,F沿竖直方向的分力与重力G平衡。正确选项为C。
答案:C
1 2 3 4 5
3.(多选)上海磁浮线路的最大转弯处半径达到8 000 m,如图所示,近距离用肉眼看几乎是一条直线,而转弯处最小半径也达到1 300 m。一个质量50 kg的乘客坐在以360 km/h的不变速率随车驶过半径2 500 m弯道,下列说法正确的是( )
A.乘客受到的向心力大小约为200 N
B.乘客受到的向心力大小约为539 N
C.乘客受到的向心力大小约为300 N
D.弯道半径设计特别长可以使乘客在转弯时更舒适
解析:根据向心力公式 可计算出乘客受到的向
心力大小约为200 N,选项A正确,B、C错误;根据 可知,在m、v保持不变的情况下,R越大乘客所受的向心力越小,在转弯时乘客更舒适,选项D正确。
答案:AD
1 2 3 4 5
4.绳子的一端拴一个重物,用手握住另一端,使重物在光滑的水平面内做匀速圆周运动,下列判断正确的是( )
A.半径相同时,角速度越小绳越易断
B.周期相同时,半径越大绳越易断
C.线速度相等时,半径越大绳越易断
D.角速度相等时,线速度越小绳越易断
答案:B
1 2 3 4 5
5.导学号61270030(选做题)一根长0.5 m的绳,当受到0.5 N 的拉力时会被拉断。在绳的一端拴上质量为0.25 kg的小球,使它在光滑的水平面上做匀速圆周运动,求拉断绳子时的角速度。
解析:小球做匀速圆周运动,绳的拉力提供向心力,由牛顿第二定律得F=mω2l,当绳子拉断时,有
答案:2.0 rad/s
6.向心力
填一填
练一练
一、向心力(见课本第23页)
1.定义:做匀速圆周运动的物体受到指向圆心的合力。
2.方向:始终指向圆心,与线速度方向垂直。
3.公式:Fn= 或Fn=mω2r。
4.来源:
(1)向心力是按照力的作用效果命名的。
(2)匀速圆周运动中向心力可能是物体所受外力的合力,也可能是某个力的分力。
5.作用:产生向心加速度,改变线速度的方向。
填一填
练一练
二、变速圆周运动和一般的曲线运动(见课本第24页)
1.变速圆周运动
合力不指向圆心,合力F可以分解为互相垂直的两个分力。
(1)跟圆周相切的分力Ft产生切向加速度,切向加速度与物体的速度方向共线,它改变速度的大小。
(2)指向圆心的分力Fn产生向心加速度,与速度方向垂直,改变速度的方向。
填一填
练一练
2.一般的曲线运动的处理方法
(1)定义:运动轨迹既不是直线也不是圆周的曲线运动。
(2)处理方法:一般的曲线运动中,可以把曲线分割成许多很短的小段,每一小段可看作一小段圆弧,研究质点在这一小段的运动时,可以采用圆周运动的处理方法进行处理,如图所示。
填一填
练一练
在水平面上转弯的摩托车(如图),向心力的来源是( )
A.重力和支持力的合力 B.静摩擦力
C.滑动摩擦力 D.重力、支持力、牵引力的合力
解析:在水平面上转弯的摩托车,竖直方向受重力和地面的支持力,水平方向受地面给摩托车的静摩擦力,静摩擦力提供车辆转弯所需的向心力,而车轮没有相对路面打滑,故该摩擦力是静摩擦力。
答案:B
问题导引
名师精讲
典例剖析
探究一
探究二
探究三
向心力的大小、方向和来源?
汽车在水平路面上保持速度大小不变,请思考汽车转弯时的向心力是由什么力提供的。
问题导引
名师精讲
典例剖析
探究一
探究二
探究三
1.向心力的作用效果
改变线速度的方向。由于向心力始终指向圆心,其方向与物体运动方向始终垂直,故向心力不改变线速度的大小。
2.向心力的特点
①方向时刻在变化,总是与线速度的方向垂直。②在匀速圆周运动中,向心力大小不变,向心力是变力,是一个按效果命名的力。
3.向心力的大小
问题导引
名师精讲
典例剖析
探究一
探究二
探究三
4.向心力的来源
问题导引
名师精讲
典例剖析
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
探究一
探究二
探究三
【例题1】 (多选)如图所示,小物体m与圆盘保持相对静止,随盘一起做匀速圆周运动,则物体的受力情况是( )
A.受重力、支持力、静摩擦力和向心力的作用
B.摩擦力的方向始终指向圆心O
C.重力和支持力是一对平衡力
D.摩擦力是使物体做匀速圆周运动的向心力
解析:分析圆盘上小物体的受力情况。竖直方向,受到重力和支持力作用,处于平衡状态;水平方向,物体随圆盘做圆周运动,由摩擦力提供向心力,故摩擦力方向指向圆心,选项B、C、D正确。
答案:BCD
问题导引
名师精讲
典例剖析
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
探究一
探究二
探究三
变式训练1 导学号61270027有一个惊险的杂技节目叫“飞车走壁”,杂技演员骑摩托车先在如图所示的大型圆筒底部做速度较小、半径较小的圆周运动,通过逐步加速,圆周运动的半径逐步增大,最后能以较大的速度在竖直的壁上做匀速圆周运动,这时使车子和人整体做匀速圆周运动的向心力是 ( )
A.圆筒壁对车的静摩擦力
B.筒壁对车的弹力
C.摩托车本身的动力
D.重力和摩擦力的合力
问题导引
名师精讲
典例剖析
探究一
探究二
探究三
解析:在竖直的壁上的摩托车只受三个力作用,其中竖直方向上重力与摩擦力是一对平衡力,水平方向上筒壁对车的弹力提供了车子和人整体做匀速圆周运动的向心力,选项B正确。
答案:B
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
匀速圆周运动的特点及解题方法?
飞机在空中水平面内做匀速圆周运动,如图所示。试分析:
(1)飞机受到哪些力的作用?向心力有谁提供?
(2)若知道飞机做圆周运动的半径,如何求得飞机运动的速度大小?
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
1.匀速圆周运动的特点
线速度大小不变,方向时刻改变;角速度、周期、频率都恒定不变;向心加速度和向心力大小都恒定不变,但方向时刻改变。
2.匀速圆周运动的性质
(1)线速度仅大小不变而方向时刻改变,是变速运动。
(2)向心加速度仅大小恒定而方向时刻改变,是非匀变速曲线运动。
(3)匀速圆周运动具有周期性,即每经过一个周期物体都要重新回到原来的位置,其运动状态(如v、a大小及方向)也要重复原来的情况。
(4)做匀速圆周运动的物体所受外力的合力大小恒定,方向总是沿半径指向圆心。
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
3.匀速圆周运动问题的解题步骤
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
【例题2】导学号61270028如图所示,双人花样滑冰运动中男运动员拉着女运动员做圆锥摆运动的精彩场面,观众有时会看到女运动员被男运动员拉着离开冰面在空中做水平方向的匀速圆周运动。若女运动员做圆锥摆运动时和竖直方向的夹角约为θ,女运动员的质量为m,转动过程中女运动员的重心做匀速圆周运动的半径为r,求:
(1)男运动员对女运动员的拉力大小。
(2)男运动员转动的角速度。
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
点拨以女运动员为研究对象,受到重力和男运动员对她的拉力作用,这两个力的合力提供向心力,其做圆周运动的平面在水平面内。根据牛顿第二定律求解。
解析:设男运动员对女运动员的拉力大小为F,女运动员受力如图所示,
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
变式训练2 如图所示,质量为1 kg的小球用细绳悬挂于O点,将小球拉离竖直位置释放后,到达最低点时的速度为 2 m/s,已知球心到悬点的距离为1 m,重力加速度g取10 m/s2,求小球在最低点时对绳的拉力的大小。
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
解析:小球在最低点时做圆周运动的向心力由重力mg和绳的拉力FT提供(如图所示)
根据牛顿第二定律有
解得FT=14 N
由牛顿第三定律知,小球在最低点时对绳的拉力大小为14 N。
答案:14 N
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
4.圆周运动中的连接体问题
(1)圆周运动中的连接体问题处理方法:此类问题的处理方法与单个物体的情况基本相同。因系统内的每个物体的速度、加速度不同,即运动状态不同,所以处理时应隔离每个物体进行分析。若物体存在加速度,应根据牛顿第二定律列方程求解;若物体处于平衡状态,应结合平衡条件进行处理。
(2)圆周运动中的连接体问题的几种典型情景
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
【例题3】导学号61270029如图所示,OM=MN=R。两个小球质量都是m,a、b为水平轻绳。两小球正随水平圆盘以角速度ω匀速同步转动。小球和圆盘间的摩擦力可以不计。求:
(1)绳b对小球N的拉力大小。
(2)绳a对小球M的拉力大小。
点拨两球所受的重力和水平面的支持力在竖直面内,且是一对平衡力,不能提供向心力。M球所受到的向心力由绳a和绳b的拉力的合力提供,N球所受到的向心力由杆的绳b的拉力提供。
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
解析:(1)对球N,受力如图所示,
其做圆周运动的半径为2R,
根据牛顿第二定律有
Fb=mω2·2R=2mω2R。
(2)对球M,受力如图所示,
其做圆周运动的半径为R,
根据牛顿第二定律有
Fa-Fb'=mω2R
Fb=Fb'
解得Fa=Fb+mω2R=3mω2R。
答案:(1)2mω2R (2)3mω2R
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
名师精讲
典例剖析
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
变速圆周运动和一般曲线的运动?
如图所示,荡秋千是小朋友很喜欢的游戏,当秋千由上向下荡时,(1)此时小朋友做的是匀速圆周运动还是变速圆周运动?(2)绳子拉力与重力的合力指向悬挂点吗?
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
1.匀速圆周运动和变速圆周运动的区别
(1)由做曲线运动的条件可知,变速圆周运动中物体所受的合力与速度方向一定不垂直,当速率增大时,物体受到的合力与瞬时速度之间的夹角是锐角;当速率减小时,物体受到的合力与速度之间的夹角是钝角。
(2)匀速圆周运动和变速圆周运动受力情况的不同是:匀速圆周运动中,合力全部用来提供向心力,合力指向圆心;变速圆周运动中,合力沿着半径方向的分量提供向心力,合力通常不指向圆心。
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
2.一般的曲线运动
运动轨迹既不是直线也不是圆周的曲线运动,称为一般曲线运动,在复杂的曲线运动中取一小段研究,每一小段都可以看成是圆周的一部分,这些圆弧的弯曲程度不同,圆心不同,注意到这个区别以后,在分析质点经过曲线上某位置的运动时,就可以采用圆周运动的方法进行研究,如图所示。
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
【例题4】 一般的曲线运动可以分成很多小段,每小段都可以看成圆周运动的一部分,即把整条曲线用一系列不同半径的小圆弧来代替。如图甲所示,曲线上的A点的曲率圆定义为:通过A点和曲线上紧邻A点两侧的两点作一圆,在极限情况下,这个圆就叫作A点的曲率圆,其半径ρ叫作A点的曲率半径。现将一物体沿与水平面成α角的方向以速度v0抛出,如图乙所示。则在其轨迹最高点P处的曲率半径是( )
探究一
探究二
探究三
问题导引
名师精讲
典例剖析
解析:根据运动的分解,物体在最高点的速度等于水平分速度,即为v0cos α,在最高点看成是向心力为重力的圆周运动的一部分,则
答案:C
1 2 3 4 5
1.(多选)关于向心力,下列说法正确的是( )
A.向心力是一种效果力
B.向心力是一种具有某种性质的力
C.向心力既可以改变速度的方向,又可以改变速度的大小
D.向心力只改变速度的方向,不改变速度的大小
解析:向心力是按作用效果命名的,是一种效果力,它可以由重力、弹力、摩擦力等性质的力提供,所以选项A正确,B错误;由于向心力始终沿半径指向圆心,与速度的方向垂直,即向心力不改变速度的大小,只改变速度的方向,因此选项C错误,D正确。
答案:AD
1 2 3 4 5
2.如图所示,将一质量为m的摆球用长为L的细绳吊起,上端固定,使摆球在水平面内做匀速圆周运动,细绳就会沿圆锥面旋转,这样就构成了一个圆锥摆。关于摆球的受力情况,下列说法中正确的是( )
A.摆球受重力、拉力和向心力的作用
B.摆球受拉力和向心力的作用
C.摆球受重力和拉力的作用
D.摆球受重力和向心力的作用
解析:物体只受重力G和拉力F的作用,而向心力是重力和拉力的合力。也可以认为向心力就是F沿水平方向的分力,显然,F沿竖直方向的分力与重力G平衡。正确选项为C。
答案:C
1 2 3 4 5
3.(多选)上海磁浮线路的最大转弯处半径达到8 000 m,如图所示,近距离用肉眼看几乎是一条直线,而转弯处最小半径也达到1 300 m。一个质量50 kg的乘客坐在以360 km/h的不变速率随车驶过半径2 500 m弯道,下列说法正确的是( )
A.乘客受到的向心力大小约为200 N
B.乘客受到的向心力大小约为539 N
C.乘客受到的向心力大小约为300 N
D.弯道半径设计特别长可以使乘客在转弯时更舒适
解析:根据向心力公式 可计算出乘客受到的向
心力大小约为200 N,选项A正确,B、C错误;根据 可知,在m、v保持不变的情况下,R越大乘客所受的向心力越小,在转弯时乘客更舒适,选项D正确。
答案:AD
1 2 3 4 5
4.绳子的一端拴一个重物,用手握住另一端,使重物在光滑的水平面内做匀速圆周运动,下列判断正确的是( )
A.半径相同时,角速度越小绳越易断
B.周期相同时,半径越大绳越易断
C.线速度相等时,半径越大绳越易断
D.角速度相等时,线速度越小绳越易断
答案:B
1 2 3 4 5
5.导学号61270030(选做题)一根长0.5 m的绳,当受到0.5 N 的拉力时会被拉断。在绳的一端拴上质量为0.25 kg的小球,使它在光滑的水平面上做匀速圆周运动,求拉断绳子时的角速度。
解析:小球做匀速圆周运动,绳的拉力提供向心力,由牛顿第二定律得F=mω2l,当绳子拉断时,有
答案:2.0 rad/s
