2019-2020学年人教版七年级下册数学5.2平行线课时训练(word版)(含解析)
文档属性
| 名称 | 2019-2020学年人教版七年级下册数学5.2平行线课时训练(word版)(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 180.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-06 00:00:00 | ||
图片预览



文档简介
2019-2020学年人教版七年级下册数学5.2平行线线课时训练
选择题(每题四个选项中只有一个选项是正确的,共12题)
1.如图,若AB∥CD,CD∥EF,那么AB和EF的位置关系是(?? )
A.平行 B.相交 C.垂直 D.不能确定
2.如果a//b,b//c,那么a//c,这个推理的依据是 ( )
A.等量代换 B.经过直线外一点,有且只有一条直线与已知直线平行
C.平行线的定义 D.平行于同一直线的两直线平行
3.如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
A.∠1=∠3 B.∠2+∠4=180° C.∠1=∠4 D.∠3=∠4
4.下列说法错误的有( )(1)相等的角是对顶角;(2)同旁内角互补;(3)同角或等角的余角相等;(4)平行于同一直线的两条直线互相平行;(5)垂直于同一条直线的两条直线互相平行;(6)过一点有且只有一条直线与已知直线平行;
A.5个 B.2个 C.3个 D.4个
5.如图,直线a、b都与直线c相交,给出下列条件:(1)∠1=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断的是( )
A.(1)、(3) B.(2)、(4)
C.(1)、(3)、(4) D.(1)、(2)、(3)、(4)
6.如图,给出下面的推理:①因为,所以;②因为,所以③因为,所以;④因为,所以.其中正确的推理是( )
A.①②③ B.①②④ C.①③④ D.②③④
7.如图,已知直线EF⊥MN垂足为F,且∠1=140°,则当∠2等于( )时,AB∥CD.
A.50° B.40° C.30° D.60°
8.如图,木工师傅在一块木板上画两条平行线,方法是:用角尺画木板边缘的两条垂线,这样画的理由有下列4种说法:其中正确的是( )
①同位角相等,两直线平行;
②内错角相等,两直线平行;
③同旁内角互补,两直线平行;
④平面内垂直于同一直线的两条直线平行.
A.①②③
B.①②④
C.①③④
D.①③
9.下列命题:①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③同旁内角互补;④垂直于同一条直线的两条直线垂直.其中的假命题有( )
A.4 个 B.3 个 C.2 个 D.1 个
10.对于同一平面内的三条直线a,b,c,给出下列5个论断:
①a∥b;②b∥c;③a∥c;④a⊥b;⑤a⊥c.
以其中两个论断作为题设,一个论断作为结论,组成一个你认为不正确的命题是( )
A.已知①②则③ B.已知②⑤则④ C.已知②④则③ D.已知④⑤则②
11.在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为4cm,b与c的距离为1cm,则a与c的距离为( )
A.1cm B.3cm C.5cm或3cm D.1cm或3cm
12.下列说法中正确的个数有( )
①两条直线被第三条直线所截,内错角相等;
②在同一平面内不重合的两条直线有平行、相交和垂直三种位置关系;
③直线外一点到这条直线的垂线段的长度叫做点到直线的距离;
④在同一平面内,垂直于同一条直线的两条直线互相平行.
A.1个 B.2个 C.3个 D.4个
二、填空题
13.在同一平面内,若直线a∥c,b∥c,则a_____b.
14.在间一平面内,有2019条互不重合的直线,l1,l2,l3,…,l2019,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5,以此类推,则l1和l2019的位置关系是_____.
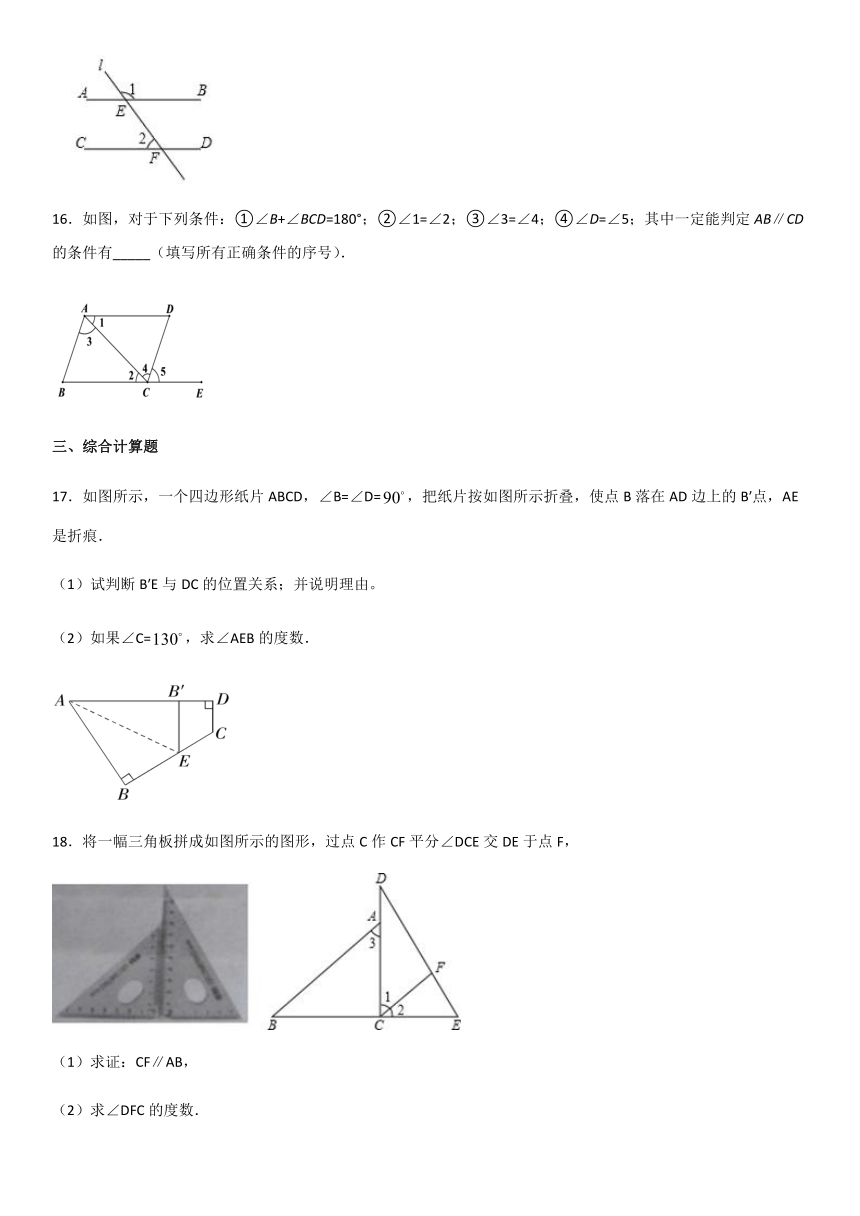
15.如图,直线l与直线AB、CD分别相交于E、F,∠1=120°,当∠2=_____时,AB∥CD.
16.如图,对于下列条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠D=∠5;其中一定能判定AB∥CD的条件有_____(填写所有正确条件的序号).
三、综合计算题
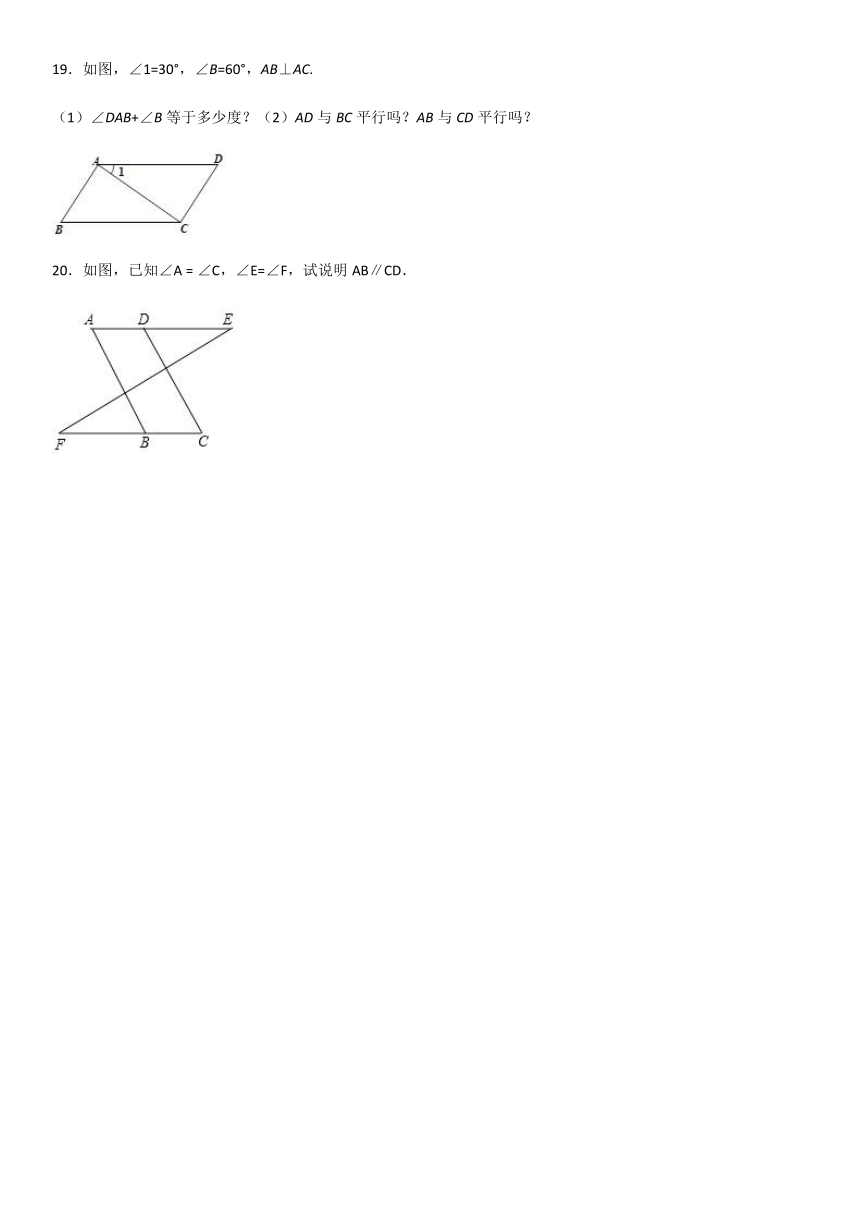
17.如图所示,一个四边形纸片ABCD,∠B=∠D=,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕.
(1)试判断B′E与DC的位置关系;并说明理由。
(2)如果∠C=,求∠AEB的度数.
18.将一幅三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,
(1)求证:CF∥AB,
(2)求∠DFC的度数.
19.如图,∠1=30°,∠B=60°,AB⊥AC.
(1)∠DAB+∠B等于多少度?(2)AD与BC平行吗?AB与CD平行吗?
20.如图,已知∠A = ∠C,∠E=∠F,试说明AB∥CD.
2019-2020学年人教版七年级下册数学5.2平行线课时训练参考答案
1.A
【解析】
解:∵AB∥CD,CD∥EF,
∴AB∥EF,(平行线的传递性)
故选A.
2.D
【解析】
如果a∥b,b∥c,那么a∥c,这个推理的依据是平行于同一直线的两直线平行.
故选D.
3.D
【解析】
A.∵∠1=∠3,∴a∥b,故A正确;
B.∵∠2+∠4=180°,∠2+∠1=180°,∴∠1=∠4,∵∠4=∠3,∴∠1=∠3,∴a∥b,故B正确;
C. ∵∠1=∠4,∠4=∠3,∴∠1=∠3,∴a∥b,故C正确;
D.∠3和∠4是对顶角,不能判断a与b是否平行,故D错误.
故选D.
4.C
【解析】
(1)相等的角是对顶角,错误;
(2)同旁内角互补,错误;
(3)同角或等角的余角相等,正确;
(4)平行于同一直线的两条直线互相平行,正确;
(5)垂直于同一条直线的两条直线互相平行,条件缺少在同一平面内,错误;
(6)过一点有且只有一条直线与已知直线平行,正确.
错误的有3个,故答案为C.
5.D
【解析】
(1)∵∠1=∠2,∴a∥b;
(2)∵∠3=∠6,∴a∥b;
(3)∵∠4+∠7=180°,∠4+∠2=180°,
∴∠7=∠2,
∴a∥b;
(4)∵∠5+∠8=180°,∠5+∠7=180°,
∴∠7=∠8,
∴a∥b.
综上所述,4个条件都能判定a∥b.
故选D.
6.B
【解析】
解:①因为∠B=∠BEF,所以AB∥EF,正确;
②因为∠B=∠CDE,所以AB∥CD,正确;
③因为∠DCE+∠AEF=180°,所以CD∥EF,故本小题错误;
④因为∠A+∠AEF=180°,所以AB∥EF,正确.
综上所述,正确的推理是①②④.
故选:B.
7.A
【解析】
解:∵AB∥CD,
∴∠3=∠4(两直线平行,同位角相等);
又∵∠1+∠3=180°(平角的定义),
∠1=140°(已知),
∴∠3=∠4=40°;
∵EF⊥MN,
∴∠2+∠4=90°,
∴∠2=50°;
故选A.
8.C
【解析】
解:如图
∵∠1=∠2=90°
∴∠1+∠2=180°,
∴a//b;
∵∠1=∠3=90°
∴a//b;
∵a⊥c,b⊥c,
∴a//b
故①③④正确;
故选C
9.A
【解析】
解:①过直线外一点有且只有一条直线与已知直线平行,故①是假命题.
②在同一个平面内,过一点有且只有一条直线与已知直线垂直,故②是假命题.
③两直线平行,同旁内角互补,故③是假命题.
④在同一个平面内,垂直于同一条直线的两条直线相互平行,故④是假命题.
故选:A
10.C
【解析】
A.根据平行线的传递性,由①②可得到③,所以A为真命题;
B.根据平行线的性质和垂直的定义,由②⑤可得④,所以B为真命题;
C.根据平行线的性质和垂直的定义,由②④可得b⊥c,所以C为假命题;
D.根据平行线的判定,由④⑤可得②,所以D为真命题.
故选:C.
11.C
【解析】分析:分类讨论:当直线c在a、b之间或直线c不在a、b之间,然后利用平行线间的距离的意义分别求解.
详解:当直线c在a、b之间时,
∵a、b、c是三条平行直线,
而a与b的距离为4cm,b与c的距离为1cm,
∴a与c的距离=4-1=3(cm);
当直线c不在a、b之间时,
∵a、b、c是三条平行直线,
而a与b的距离为4cm,b与c的距离为1cm,
∴a与c的距离=4+1=5(cm),
综上所述,a与c的距离为3cm或5cm.
故选:C.
12.B
【解析】
解:两直线平行内错角相等,故①错误;在同一平面内不重合的两条直线有平行和相交两种位置关系,故②错误;直线外一点到这条直线的垂线段的长度叫做点到直线的距离,故③正确;在同一平面内,根据同位角相等两直线平行可知④正确;故选B.
13.∥
【解析】
解:∵a∥c,b∥c,
∴a∥b(平行于同一直线的两条直线互相平行).
故答案为:∥.
14.l1⊥l2019.
【解析】
l1与l2019的位置关系为:l1∥l2008.
理由:∵l1⊥l2,l2∥l3,
∴l1⊥l3,
∵l3⊥l4,
∴l1∥l4,
∵l4∥l5,
∴l1∥l5,
∵l5⊥l6,
∴l1⊥l6,
∵l6∥l7,
∴l1⊥l7,
∴可得规律为:l1⊥l2,l1⊥l3,l1∥l4,l1∥l5,
l1⊥l6,l1⊥l7,l1∥l8,l1∥l9,
…,
则 l1∥l4,l1∥l5,l1∥l8,l1∥l9,l1∥l12,l1∥l13,l1∥l16,l1∥l17…
l1⊥l2,l1⊥l3,l1⊥l6,l1⊥l7,l1⊥l10,l1⊥l11,l1⊥l14,l1⊥l15,…
∵2019÷4=504…3
∴l1⊥l2019.
故答案为l1⊥l2019.
15.60°
【解析】
如图:
若AB∥CD,则∠2+∠3=180°,
∵∠1=∠3,
∴∠2+∠1=180°,
∵∠1=120°,
∴∠2=60°,
∴当∠2=60°时,AB∥CD.
故答案为:60°.
16.①③
【解析】
①∵∠B+∠BCD=180°,
∴AB∥CD;
②∵∠1=∠2,
∴AD∥CB;
③∵∠3=∠4,
∴AB∥CD;
④∵∠D=∠5,
∴AD∥BC,
所以一定能判定AB//CD的有①③,
故答案为①③.
17.(1)B/E//CD;(2)∠AEB=65°;
【解析】
(1)B′E∥DC,
证明:由折叠得:∠AB′E=∠B=∠D=90°,
∴B′E∥DC;
(2)解:∵B′E∥DC,∠C=1130°,
∴∠B′EB=130°,
由折叠得:∠AEB=∠AEB′=×130°=65°.
18.(1)证明见解析;(2)105°
【解析】
解:(1)证明:∵CF平分∠DCE,
∴∠1=∠2=∠DCE.
∵∠DCE=90°,
∴∠1=45°.
∵∠3=45°,
∴∠1=∠3.
∴AB∥CF.
(2)∵∠D=30°,∠1=45°,
∴∠DFC=180°﹣30°﹣45°=105°.
19.解:(1)180°;(2)无法确定AB与CD的关系.
【解析】
①∵AB⊥AC,∴∠BAC=90°.
又∠1=30°,∴∠BAD=120°.
∵∠B=60°,∴∠DAB+∠B=180°.
②答:AD∥BC,AB与CD不一定平行.理由是:
∵∠DAB+∠B=180°
∴AD∥BC
∵∠ACD不能确定,
∴AB与CD不一定平行.
20.【解析】
证明:∵∠E=∠F,
∴AE∥CF,
∴∠A=∠ABF,
∵∠A=∠C,
∴∠ABF=∠C,
∴AB∥CD.
选择题(每题四个选项中只有一个选项是正确的,共12题)
1.如图,若AB∥CD,CD∥EF,那么AB和EF的位置关系是(?? )
A.平行 B.相交 C.垂直 D.不能确定
2.如果a//b,b//c,那么a//c,这个推理的依据是 ( )
A.等量代换 B.经过直线外一点,有且只有一条直线与已知直线平行
C.平行线的定义 D.平行于同一直线的两直线平行
3.如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
A.∠1=∠3 B.∠2+∠4=180° C.∠1=∠4 D.∠3=∠4
4.下列说法错误的有( )(1)相等的角是对顶角;(2)同旁内角互补;(3)同角或等角的余角相等;(4)平行于同一直线的两条直线互相平行;(5)垂直于同一条直线的两条直线互相平行;(6)过一点有且只有一条直线与已知直线平行;
A.5个 B.2个 C.3个 D.4个
5.如图,直线a、b都与直线c相交,给出下列条件:(1)∠1=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断的是( )
A.(1)、(3) B.(2)、(4)
C.(1)、(3)、(4) D.(1)、(2)、(3)、(4)
6.如图,给出下面的推理:①因为,所以;②因为,所以③因为,所以;④因为,所以.其中正确的推理是( )
A.①②③ B.①②④ C.①③④ D.②③④
7.如图,已知直线EF⊥MN垂足为F,且∠1=140°,则当∠2等于( )时,AB∥CD.
A.50° B.40° C.30° D.60°
8.如图,木工师傅在一块木板上画两条平行线,方法是:用角尺画木板边缘的两条垂线,这样画的理由有下列4种说法:其中正确的是( )
①同位角相等,两直线平行;
②内错角相等,两直线平行;
③同旁内角互补,两直线平行;
④平面内垂直于同一直线的两条直线平行.
A.①②③
B.①②④
C.①③④
D.①③
9.下列命题:①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③同旁内角互补;④垂直于同一条直线的两条直线垂直.其中的假命题有( )
A.4 个 B.3 个 C.2 个 D.1 个
10.对于同一平面内的三条直线a,b,c,给出下列5个论断:
①a∥b;②b∥c;③a∥c;④a⊥b;⑤a⊥c.
以其中两个论断作为题设,一个论断作为结论,组成一个你认为不正确的命题是( )
A.已知①②则③ B.已知②⑤则④ C.已知②④则③ D.已知④⑤则②
11.在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为4cm,b与c的距离为1cm,则a与c的距离为( )
A.1cm B.3cm C.5cm或3cm D.1cm或3cm
12.下列说法中正确的个数有( )
①两条直线被第三条直线所截,内错角相等;
②在同一平面内不重合的两条直线有平行、相交和垂直三种位置关系;
③直线外一点到这条直线的垂线段的长度叫做点到直线的距离;
④在同一平面内,垂直于同一条直线的两条直线互相平行.
A.1个 B.2个 C.3个 D.4个
二、填空题
13.在同一平面内,若直线a∥c,b∥c,则a_____b.
14.在间一平面内,有2019条互不重合的直线,l1,l2,l3,…,l2019,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5,以此类推,则l1和l2019的位置关系是_____.
15.如图,直线l与直线AB、CD分别相交于E、F,∠1=120°,当∠2=_____时,AB∥CD.
16.如图,对于下列条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠D=∠5;其中一定能判定AB∥CD的条件有_____(填写所有正确条件的序号).
三、综合计算题
17.如图所示,一个四边形纸片ABCD,∠B=∠D=,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕.
(1)试判断B′E与DC的位置关系;并说明理由。
(2)如果∠C=,求∠AEB的度数.
18.将一幅三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,
(1)求证:CF∥AB,
(2)求∠DFC的度数.
19.如图,∠1=30°,∠B=60°,AB⊥AC.
(1)∠DAB+∠B等于多少度?(2)AD与BC平行吗?AB与CD平行吗?
20.如图,已知∠A = ∠C,∠E=∠F,试说明AB∥CD.
2019-2020学年人教版七年级下册数学5.2平行线课时训练参考答案
1.A
【解析】
解:∵AB∥CD,CD∥EF,
∴AB∥EF,(平行线的传递性)
故选A.
2.D
【解析】
如果a∥b,b∥c,那么a∥c,这个推理的依据是平行于同一直线的两直线平行.
故选D.
3.D
【解析】
A.∵∠1=∠3,∴a∥b,故A正确;
B.∵∠2+∠4=180°,∠2+∠1=180°,∴∠1=∠4,∵∠4=∠3,∴∠1=∠3,∴a∥b,故B正确;
C. ∵∠1=∠4,∠4=∠3,∴∠1=∠3,∴a∥b,故C正确;
D.∠3和∠4是对顶角,不能判断a与b是否平行,故D错误.
故选D.
4.C
【解析】
(1)相等的角是对顶角,错误;
(2)同旁内角互补,错误;
(3)同角或等角的余角相等,正确;
(4)平行于同一直线的两条直线互相平行,正确;
(5)垂直于同一条直线的两条直线互相平行,条件缺少在同一平面内,错误;
(6)过一点有且只有一条直线与已知直线平行,正确.
错误的有3个,故答案为C.
5.D
【解析】
(1)∵∠1=∠2,∴a∥b;
(2)∵∠3=∠6,∴a∥b;
(3)∵∠4+∠7=180°,∠4+∠2=180°,
∴∠7=∠2,
∴a∥b;
(4)∵∠5+∠8=180°,∠5+∠7=180°,
∴∠7=∠8,
∴a∥b.
综上所述,4个条件都能判定a∥b.
故选D.
6.B
【解析】
解:①因为∠B=∠BEF,所以AB∥EF,正确;
②因为∠B=∠CDE,所以AB∥CD,正确;
③因为∠DCE+∠AEF=180°,所以CD∥EF,故本小题错误;
④因为∠A+∠AEF=180°,所以AB∥EF,正确.
综上所述,正确的推理是①②④.
故选:B.
7.A
【解析】
解:∵AB∥CD,
∴∠3=∠4(两直线平行,同位角相等);
又∵∠1+∠3=180°(平角的定义),
∠1=140°(已知),
∴∠3=∠4=40°;
∵EF⊥MN,
∴∠2+∠4=90°,
∴∠2=50°;
故选A.
8.C
【解析】
解:如图
∵∠1=∠2=90°
∴∠1+∠2=180°,
∴a//b;
∵∠1=∠3=90°
∴a//b;
∵a⊥c,b⊥c,
∴a//b
故①③④正确;
故选C
9.A
【解析】
解:①过直线外一点有且只有一条直线与已知直线平行,故①是假命题.
②在同一个平面内,过一点有且只有一条直线与已知直线垂直,故②是假命题.
③两直线平行,同旁内角互补,故③是假命题.
④在同一个平面内,垂直于同一条直线的两条直线相互平行,故④是假命题.
故选:A
10.C
【解析】
A.根据平行线的传递性,由①②可得到③,所以A为真命题;
B.根据平行线的性质和垂直的定义,由②⑤可得④,所以B为真命题;
C.根据平行线的性质和垂直的定义,由②④可得b⊥c,所以C为假命题;
D.根据平行线的判定,由④⑤可得②,所以D为真命题.
故选:C.
11.C
【解析】分析:分类讨论:当直线c在a、b之间或直线c不在a、b之间,然后利用平行线间的距离的意义分别求解.
详解:当直线c在a、b之间时,
∵a、b、c是三条平行直线,
而a与b的距离为4cm,b与c的距离为1cm,
∴a与c的距离=4-1=3(cm);
当直线c不在a、b之间时,
∵a、b、c是三条平行直线,
而a与b的距离为4cm,b与c的距离为1cm,
∴a与c的距离=4+1=5(cm),
综上所述,a与c的距离为3cm或5cm.
故选:C.
12.B
【解析】
解:两直线平行内错角相等,故①错误;在同一平面内不重合的两条直线有平行和相交两种位置关系,故②错误;直线外一点到这条直线的垂线段的长度叫做点到直线的距离,故③正确;在同一平面内,根据同位角相等两直线平行可知④正确;故选B.
13.∥
【解析】
解:∵a∥c,b∥c,
∴a∥b(平行于同一直线的两条直线互相平行).
故答案为:∥.
14.l1⊥l2019.
【解析】
l1与l2019的位置关系为:l1∥l2008.
理由:∵l1⊥l2,l2∥l3,
∴l1⊥l3,
∵l3⊥l4,
∴l1∥l4,
∵l4∥l5,
∴l1∥l5,
∵l5⊥l6,
∴l1⊥l6,
∵l6∥l7,
∴l1⊥l7,
∴可得规律为:l1⊥l2,l1⊥l3,l1∥l4,l1∥l5,
l1⊥l6,l1⊥l7,l1∥l8,l1∥l9,
…,
则 l1∥l4,l1∥l5,l1∥l8,l1∥l9,l1∥l12,l1∥l13,l1∥l16,l1∥l17…
l1⊥l2,l1⊥l3,l1⊥l6,l1⊥l7,l1⊥l10,l1⊥l11,l1⊥l14,l1⊥l15,…
∵2019÷4=504…3
∴l1⊥l2019.
故答案为l1⊥l2019.
15.60°
【解析】
如图:
若AB∥CD,则∠2+∠3=180°,
∵∠1=∠3,
∴∠2+∠1=180°,
∵∠1=120°,
∴∠2=60°,
∴当∠2=60°时,AB∥CD.
故答案为:60°.
16.①③
【解析】
①∵∠B+∠BCD=180°,
∴AB∥CD;
②∵∠1=∠2,
∴AD∥CB;
③∵∠3=∠4,
∴AB∥CD;
④∵∠D=∠5,
∴AD∥BC,
所以一定能判定AB//CD的有①③,
故答案为①③.
17.(1)B/E//CD;(2)∠AEB=65°;
【解析】
(1)B′E∥DC,
证明:由折叠得:∠AB′E=∠B=∠D=90°,
∴B′E∥DC;
(2)解:∵B′E∥DC,∠C=1130°,
∴∠B′EB=130°,
由折叠得:∠AEB=∠AEB′=×130°=65°.
18.(1)证明见解析;(2)105°
【解析】
解:(1)证明:∵CF平分∠DCE,
∴∠1=∠2=∠DCE.
∵∠DCE=90°,
∴∠1=45°.
∵∠3=45°,
∴∠1=∠3.
∴AB∥CF.
(2)∵∠D=30°,∠1=45°,
∴∠DFC=180°﹣30°﹣45°=105°.
19.解:(1)180°;(2)无法确定AB与CD的关系.
【解析】
①∵AB⊥AC,∴∠BAC=90°.
又∠1=30°,∴∠BAD=120°.
∵∠B=60°,∴∠DAB+∠B=180°.
②答:AD∥BC,AB与CD不一定平行.理由是:
∵∠DAB+∠B=180°
∴AD∥BC
∵∠ACD不能确定,
∴AB与CD不一定平行.
20.【解析】
证明:∵∠E=∠F,
∴AE∥CF,
∴∠A=∠ABF,
∵∠A=∠C,
∴∠ABF=∠C,
∴AB∥CD.
