北师大版七年级数学下册5.3.1等腰三角形的性质课件 (共22张PPT)
文档属性
| 名称 | 北师大版七年级数学下册5.3.1等腰三角形的性质课件 (共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-07 23:20:44 | ||
图片预览







文档简介
课件22张PPT。第五章 生活中的轴对称 教学目标
1.理解并掌握等腰三角形的性质;(重点)
2.探索并掌握等腰三角形的轴对称性及其相关性质,能初步运用其解决有关问题.(难点).
2.等腰三角形的性质
(1)等腰三角形的两个底角相等(简写成“等边对等角”).
(2)等腰三角形顶角的平分线、底边上的中线、底边上的高重合(简称“三线合一”),
其所在的直线是等腰三角形的对称轴.
(3)等腰三角形是以顶角的平分线(底边上的中线、底边上的高)所在直线为对称轴的轴对称图形,
通常只有一条对称轴.1.等腰三角形的定义
有两条边相等的三角形是等腰三角形.相等的两条边叫做腰,另一条边叫做底边,
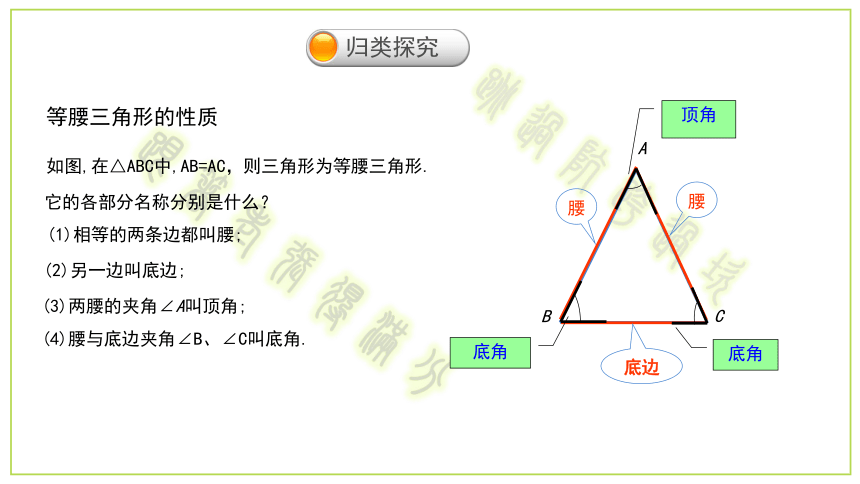
两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.如图注意:(1)“等边对等角”是在同一个三角形中,否则,不能使用该性质.
(2)等腰三角形“三线合一”的应用非常广泛,它可以用来得到角相等、线段相等、垂直关系等.
(3)等腰三角形的对称轴是直线.3.等边三角形
(1)等边三角形的概念:三边都相等的三角形叫做等边三角形,也叫正三角形.
(2)等边三角形的性质:
①等边三角形是轴对称图形,它有三条对称轴.
②等边三角形的三个内角都相等,并且每个内角都等于60°.如图,在△ABC中,AB=AC,则三角形为等腰三角形.它的各部分名称分别是什么?(1)相等的两条边都叫腰;(2)另一边叫底边;(3)两腰的夹角∠A叫顶角;(4)腰与底边夹角∠B、∠C叫底角.等腰三角形的性质1.等腰三角形是轴对称图形吗?找出对称轴.2.顶角的平分线所在的直线是等腰三角形的对称轴吗?3.底边上的中线所在的直线是等腰三角形的对称轴吗?底边上的高所在直线呢?4.沿对称轴对折,你能发现等腰三角形的哪些特征?说说你的理由. 等腰三角形是一类特殊的三角形.等腰三角形除具有一般三角形的性质外,还具有什么样的特殊性质呢?(1)等腰三角形是轴对称图形.
(2)∠B =∠C.
(3)∠BAD=∠CAD,AD为顶角的平分线.
(4)∠ADB=∠ADC=90°,AD为底边上的高.
(5)BD=CD,AD为底边上的中线.归纳:等腰三角形的两个底角相等.等腰三角形的顶角平分线、底边上的高和底边上的中线互相重合(简称“三线合一”).解:在ΔABC中,∵AD是角平分线,
∴∠BAD=∠CAD.
在ΔABD和ΔACD中,
∵AB=AC,∠BAD=∠CAD,AD=AD,
∴ΔABD≌ΔACD.
∴BD=CD, ∠ADB=∠ADC=90?.
∴AD是ΔABC的角平分线、底边上的中线、底边上的高.1.等腰三角形是轴对称图形.
2.等腰三角形的顶角平分线、底边上的中线和底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
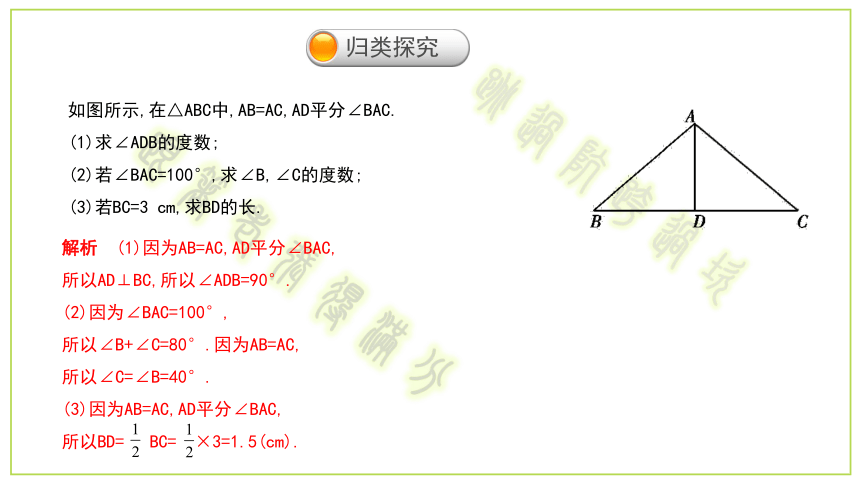
3.等腰三角形的两底角相等.等腰三角形的性质:如图所示,在△ABC中,AB=AC,AD平分∠BAC.
(1)求∠ADB的度数;
(2)若∠BAC=100°,求∠B,∠C的度数;
(3)若BC=3 cm,求BD的长.
等腰三角形的一个内角是50°,则这个三角形的底角的大小是( )
A.65°或50° B.80°或40°
C.65°或80° D.50°或80°解析:当50°的角是底角时,三角形的底角就是50°;当50°的角是顶角时,两底角相等,根据三角形的内角和定理易得底角是65°.A解 ∵AB=AC, BD=BC=AD,(已知)
∴∠ABC=∠C=∠BDC,
∠A=∠ABD.(等边对等角)
设∠A=x°,∵∠A+∠ABD+∠ADB=180°,
又∵∠BDC+∠ADB=180°,
∴∠BDC=∠A+∠ABD=2x°.
∵∠ABC=∠C=∠BDC=2x°,
∴x+2x+2x=180.(三角形内角和等于180°)
解得 x=36 .∴∠A=36°,∠C=72°.如图,在ΔABC中,AB=AC , 点D在AC上,且BD=BC=AD , 求∠A和∠C的度数.1.填空:
(1)等腰直角三角形的每一个锐角的度数是 ;
(2)如果等腰三角形的底角等于40°,那么它的顶角的度数是 ;
(3)如果等腰三角形有一个内角等于80°,那么这个三角形的最小内角等于 .
(4)△ ABC中,AB=AC,∠A= 36?,则∠B= , ∠C= .
(5)△ ABC中,AB=AC,∠B= 36?,则∠A= , ∠C= .
20°或50°100°45°72°72°108°36°方法总结:等边对等角! 2.如图,是由大小不等的等边三角形组成的图案,请找出它的对称轴.解:∵OA=AB,
∴∠ABO=∠O=15°,∴∠BAO=150°,
∴∠BAC=∠ABO+∠O=30°.
∵AB=BC,
∴∠ACB=∠BAC=30°,
∴∠CBO=135°,∴∠CBD=∠O+∠ACB=45°.
∵BC=CD,∴∠D=∠CBD=45°,∴∠BCD=90°,
∴∠1=180°-∠BCD-∠BCO=60°.3.如图,∠AOB=15°,且OA=AB=BC=CD.求∠1的度数.4.如图,在ΔABC中,AB=AC,∠BAC=120°,点D, E是底边上两点,且BD=AD,CE=AE.求∠DAE的度数.解 :∵AB=AC,∴∠B=∠C,
∴∠B=∠C=(180°-120°)÷2=30°.
又∵BD=AD,∴∠BAD=∠B=30°.
同理,∠CAE=∠C=30°.
∴∠DAE=∠BAC-∠BAD-∠CAE
=120°-30°-30°
=60°.等腰三角形的性质等腰三角形的两个底角相等(等边对等角).等腰三角形的顶角平分线、底边上的中线和底边上的高重合(三线合一).1.(山东烟台中考)某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为?( )
? A.48° ????B.40° ????C.30° ????D.24°答案????D ∵AB∥CD,∴∠DFE=∠BAF=48°.
∵CF=EF,∴∠C=∠E.
∵∠C+∠E=∠DFE=48°,∴∠C=24°.2.(浙江台州中考)如图,已知等腰三角形ABC,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是?(???? )
A.AE=EC ???? B.AE=BE
C.∠EBC=∠BAC ? ???D.∠EBC=∠ABE答案????C
∵AB=AC,∴∠ABC=∠ACB,
由题意可知BC=BE,
∴∠ACB=∠BEC,
∴∠BAC=∠EBC,故选C.3.(浙江丽水中考)等腰三角形的一个内角为100°,则顶角的度数是 ????.解析 ∵100°>90°,
∴100°的角是顶角,
故答案为100°.4.(江西中考)如图(1)是一把园林剪刀,把它抽象为图(2),其中OA=OB,若剪刀张开的角为30°,
则∠A= ????度.
?
图5-3-375解析 由对顶角相等可得∠AOB=30°,∵OA=OB,∴∠A= ?=75°.5.如图,在等边三角形ABC中,BE和CD分别是AC、AB边上的高,求∠BFC的度数.解析 ∵△ABC是等边三角形,BE、CD分别是AC、AB边上的高,
∴∠FBC=∠FCB= ×60°=30°,
∴∠BFC=180°-30°-30°=120°.
1.理解并掌握等腰三角形的性质;(重点)
2.探索并掌握等腰三角形的轴对称性及其相关性质,能初步运用其解决有关问题.(难点).
2.等腰三角形的性质
(1)等腰三角形的两个底角相等(简写成“等边对等角”).
(2)等腰三角形顶角的平分线、底边上的中线、底边上的高重合(简称“三线合一”),
其所在的直线是等腰三角形的对称轴.
(3)等腰三角形是以顶角的平分线(底边上的中线、底边上的高)所在直线为对称轴的轴对称图形,
通常只有一条对称轴.1.等腰三角形的定义
有两条边相等的三角形是等腰三角形.相等的两条边叫做腰,另一条边叫做底边,
两腰所夹的角叫做顶角,底边与腰的夹角叫做底角.如图注意:(1)“等边对等角”是在同一个三角形中,否则,不能使用该性质.
(2)等腰三角形“三线合一”的应用非常广泛,它可以用来得到角相等、线段相等、垂直关系等.
(3)等腰三角形的对称轴是直线.3.等边三角形
(1)等边三角形的概念:三边都相等的三角形叫做等边三角形,也叫正三角形.
(2)等边三角形的性质:
①等边三角形是轴对称图形,它有三条对称轴.
②等边三角形的三个内角都相等,并且每个内角都等于60°.如图,在△ABC中,AB=AC,则三角形为等腰三角形.它的各部分名称分别是什么?(1)相等的两条边都叫腰;(2)另一边叫底边;(3)两腰的夹角∠A叫顶角;(4)腰与底边夹角∠B、∠C叫底角.等腰三角形的性质1.等腰三角形是轴对称图形吗?找出对称轴.2.顶角的平分线所在的直线是等腰三角形的对称轴吗?3.底边上的中线所在的直线是等腰三角形的对称轴吗?底边上的高所在直线呢?4.沿对称轴对折,你能发现等腰三角形的哪些特征?说说你的理由. 等腰三角形是一类特殊的三角形.等腰三角形除具有一般三角形的性质外,还具有什么样的特殊性质呢?(1)等腰三角形是轴对称图形.
(2)∠B =∠C.
(3)∠BAD=∠CAD,AD为顶角的平分线.
(4)∠ADB=∠ADC=90°,AD为底边上的高.
(5)BD=CD,AD为底边上的中线.归纳:等腰三角形的两个底角相等.等腰三角形的顶角平分线、底边上的高和底边上的中线互相重合(简称“三线合一”).解:在ΔABC中,∵AD是角平分线,
∴∠BAD=∠CAD.
在ΔABD和ΔACD中,
∵AB=AC,∠BAD=∠CAD,AD=AD,
∴ΔABD≌ΔACD.
∴BD=CD, ∠ADB=∠ADC=90?.
∴AD是ΔABC的角平分线、底边上的中线、底边上的高.1.等腰三角形是轴对称图形.
2.等腰三角形的顶角平分线、底边上的中线和底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
3.等腰三角形的两底角相等.等腰三角形的性质:如图所示,在△ABC中,AB=AC,AD平分∠BAC.
(1)求∠ADB的度数;
(2)若∠BAC=100°,求∠B,∠C的度数;
(3)若BC=3 cm,求BD的长.
等腰三角形的一个内角是50°,则这个三角形的底角的大小是( )
A.65°或50° B.80°或40°
C.65°或80° D.50°或80°解析:当50°的角是底角时,三角形的底角就是50°;当50°的角是顶角时,两底角相等,根据三角形的内角和定理易得底角是65°.A解 ∵AB=AC, BD=BC=AD,(已知)
∴∠ABC=∠C=∠BDC,
∠A=∠ABD.(等边对等角)
设∠A=x°,∵∠A+∠ABD+∠ADB=180°,
又∵∠BDC+∠ADB=180°,
∴∠BDC=∠A+∠ABD=2x°.
∵∠ABC=∠C=∠BDC=2x°,
∴x+2x+2x=180.(三角形内角和等于180°)
解得 x=36 .∴∠A=36°,∠C=72°.如图,在ΔABC中,AB=AC , 点D在AC上,且BD=BC=AD , 求∠A和∠C的度数.1.填空:
(1)等腰直角三角形的每一个锐角的度数是 ;
(2)如果等腰三角形的底角等于40°,那么它的顶角的度数是 ;
(3)如果等腰三角形有一个内角等于80°,那么这个三角形的最小内角等于 .
(4)△ ABC中,AB=AC,∠A= 36?,则∠B= , ∠C= .
(5)△ ABC中,AB=AC,∠B= 36?,则∠A= , ∠C= .
20°或50°100°45°72°72°108°36°方法总结:等边对等角! 2.如图,是由大小不等的等边三角形组成的图案,请找出它的对称轴.解:∵OA=AB,
∴∠ABO=∠O=15°,∴∠BAO=150°,
∴∠BAC=∠ABO+∠O=30°.
∵AB=BC,
∴∠ACB=∠BAC=30°,
∴∠CBO=135°,∴∠CBD=∠O+∠ACB=45°.
∵BC=CD,∴∠D=∠CBD=45°,∴∠BCD=90°,
∴∠1=180°-∠BCD-∠BCO=60°.3.如图,∠AOB=15°,且OA=AB=BC=CD.求∠1的度数.4.如图,在ΔABC中,AB=AC,∠BAC=120°,点D, E是底边上两点,且BD=AD,CE=AE.求∠DAE的度数.解 :∵AB=AC,∴∠B=∠C,
∴∠B=∠C=(180°-120°)÷2=30°.
又∵BD=AD,∴∠BAD=∠B=30°.
同理,∠CAE=∠C=30°.
∴∠DAE=∠BAC-∠BAD-∠CAE
=120°-30°-30°
=60°.等腰三角形的性质等腰三角形的两个底角相等(等边对等角).等腰三角形的顶角平分线、底边上的中线和底边上的高重合(三线合一).1.(山东烟台中考)某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为?( )
? A.48° ????B.40° ????C.30° ????D.24°答案????D ∵AB∥CD,∴∠DFE=∠BAF=48°.
∵CF=EF,∴∠C=∠E.
∵∠C+∠E=∠DFE=48°,∴∠C=24°.2.(浙江台州中考)如图,已知等腰三角形ABC,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是?(???? )
A.AE=EC ???? B.AE=BE
C.∠EBC=∠BAC ? ???D.∠EBC=∠ABE答案????C
∵AB=AC,∴∠ABC=∠ACB,
由题意可知BC=BE,
∴∠ACB=∠BEC,
∴∠BAC=∠EBC,故选C.3.(浙江丽水中考)等腰三角形的一个内角为100°,则顶角的度数是 ????.解析 ∵100°>90°,
∴100°的角是顶角,
故答案为100°.4.(江西中考)如图(1)是一把园林剪刀,把它抽象为图(2),其中OA=OB,若剪刀张开的角为30°,
则∠A= ????度.
?
图5-3-375解析 由对顶角相等可得∠AOB=30°,∵OA=OB,∴∠A= ?=75°.5.如图,在等边三角形ABC中,BE和CD分别是AC、AB边上的高,求∠BFC的度数.解析 ∵△ABC是等边三角形,BE、CD分别是AC、AB边上的高,
∴∠FBC=∠FCB= ×60°=30°,
∴∠BFC=180°-30°-30°=120°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
