人教版八年级数学下册:第十九章一次函数单元教案
文档属性
| 名称 | 人教版八年级数学下册:第十九章一次函数单元教案 |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-07 23:38:07 | ||
图片预览




文档简介
八年级下册教案
第十九章一次函数
八
年
级
备
课
组
第十九章一次函数
19.1.1变量与函数(1)
教学目标
1.掌握常量和变量、自变量和函数的基本概念;
2.引导学生联系代数式和方程的相关知识,继续探索数量关系,增强数学建模意识,列出函数关系式.
教学重点:了解变量与常量的意义,充分体会运动变化过程中量的变化.
难点:能用解析法正确表示数量关系。
教学过程
1、
预习检测:
找出下面问题中变化的量和不变的量:
(1)汽车以60
km/h
的速度匀速行驶,行驶时间为
t
h,行驶路程为
s
km.
(2)每张电影票的售价为10
元,设某场电影售出x
张票,票房收入为y
元.
二、合作交流:
(1)圆形水波慢慢地扩大,在这一过程中,当圆的半径r
分别为10
cm,20
cm,30
cm
时,圆的面积S
分别为多少?在这个过程中,哪些量是变化的?
(2)用10
m长的绳子围一个矩形,当矩形的一边长x
分别为3
m,3.5
m,4
m,4.5
m
时,它的邻边长y
分别为多少?在矩形改变形状的变化过程中,哪些量是变化的?哪些量是固定不变的?
三、精讲解惑
1,常量和变量
上述运动变化过程中出现的数量,你认为可以怎样分类?
在上面的问题中,我们研究了一些数量关系,它们都刻画了某些变化规律.这里出现了各种各样的量,特别值得注意的是出现了一些数值会发生变化的量.例如问题1中,刻画气温变化规律的量是时间t和气温T,气温T随着时间t的变化而变化,它们都会取不同的数值.像这样在某一变化过程中,可以取不同数值的量,叫做变量(variable).问题的研究过程中,还有一种量,它的取值始终保持不变,我们称之为常量(constant)。
2
例1、
写出下列各问题中的关系式,并指出其中的常量与变量:
(1)圆的周长C与半径r的关系式;
(2)(2)火车以60千米/时的速度行驶,它驶过的路程s(千米)和所用时间t(时)的关系式;
(3)n边形的内角和S与边数n的关系式.
解
(1)C=2π
r,2π是常量,r、C是变量;
(2)s=60t,60是常量,t、s是变量;
(3)S=(n-2)×180,2、180是常量,n、S是变量.
4、
随堂练习:
1、指出下列变化过程中的变量和常量:
(1)
汽油的价格是7.4元/升,加油
x
L,车主加油
付油费
y
元;
(2)
小明看一本200
页的小说,看完这本小说需要
t
天,平均每天所看的页数为
n;
(3)
用长为40
cm
的绳子围矩形,围成的矩形一边
长为
x
cm,其面积为
S
cm2.
2、书71页练习
五、小结
在某个变化过程中,可以取不同数值的量,叫做变量;数值始终保持不变的量,叫做常量.例如x和y,对于x的每一个值,y都有惟一的值与之对应,我们就说x是自变量,y是因变量.
六、布置作业:
教学后记:
19.1.1变量与函数(2)
教学目标:
1.进一步体会运动变化过程中的数量变化;
2.从典型实例中抽象概括出函数的概念,了解函数的概念.
教学重点:概括并理解函数概念中的单值对应关系,用式子表示变量间的关系
教学难点:用含有一个变量的式子表示另一个变量
教学过程
一、预习检测:什么是变量?什么是常量?
二、合作交流:
问题1 下面变化过程中的变量之间有什么联系?
(1)汽车以60
km/h
的速度匀速行驶,行驶的时间为t
h,行驶的路程为s
km;
问题2 下面变化过程中的变量之间有什么联系?
(2)每张电影票的售价为10
元,设某场电影售出
x
张票,票房收入为
y
元;
(3)圆形水波慢慢地扩大,在这一过程中,圆的半径为
r
,面积为
S
;
(4)用10
m
长的绳子围一个矩形,当矩形的一边长为
x,它的邻边长为
y.
三
释疑解惑:
函数的定义:一般地,在一个变化过程中,如果有两个变量
x
与
y,并且对于
x
的每一个确定的值,y
都有唯一确定的值与其对应,那么我们就说
x
是自变量,y
是
x
的函数.如果当
x
=a
时,对应的
y
=b,那么
b
叫做当自变量的值为
a
时的函数值.
4、随堂练习:
课本P74页-75页练习
五、总结归纳:
1.函数概念包含:(1)两个变量;(2)两个变量之间的对应关系.
2.函数关系三种表示方法:(1)解析法;(2)列表法;(3)图象法.
六、布置作业
教学后记:
19.1.2函数的图象(1)
教学目标
1.了解函数图象的意义;
2.会观察函数图象获取信息,根据图象初步分析函
数的对应关系和变化规律;
3.经历画函数图象的过程,体会函数图象建立数形联系的关键是分别用点的横、纵坐标表示自变量和对应的函数值.
教学重点:函数图象的意义,从图象中获取信息.
难点:会观察函数图象获取信息,根据图象初步分析函
数的对应关系和变化规律;
教学过程
1、
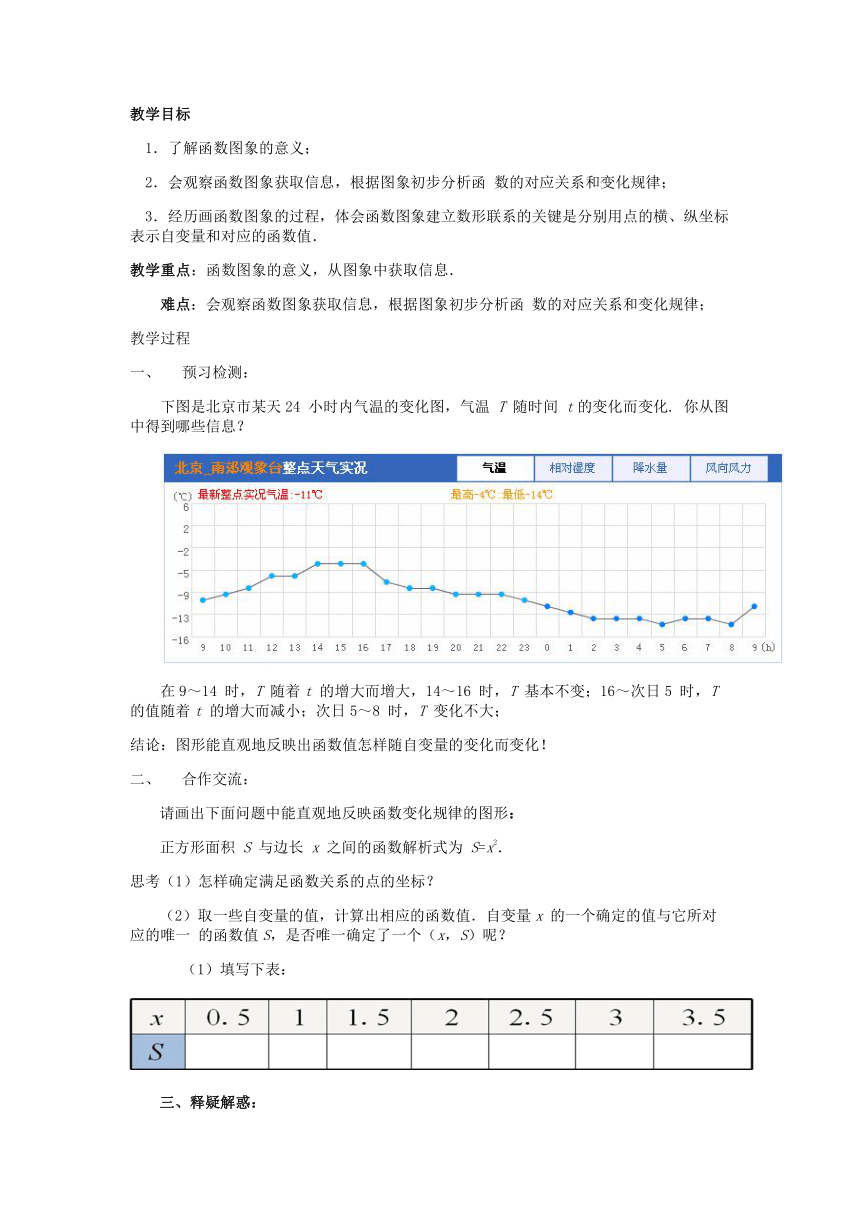
预习检测:
下图是北京市某天24
小时内气温的变化图,气温
T
随时间
t的变化而变化.
你从图中得到哪些信息?
在9~14
时,T
随着t
的增大而增大,14~16
时,T
基本不变;16~次日5
时,T
的值随着t
的增大而减小;次日5~8
时,T
变化不大;
结论:图形能直观地反映出函数值怎样随自变量的变化而变化!
2、
合作交流:
请画出下面问题中能直观地反映函数变化规律的图形:
正方形面积
S
与边长
x
之间的函数解析式为
S=x2.
思考(1)怎样确定满足函数关系的点的坐标?
(2)取一些自变量的值,计算出相应的函数值.自变量x
的一个确定的值与它所对应的唯一
的函数值S,是否唯一确定了一个(x,S)呢?
(1)填写下表:
三、释疑解惑:
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.如右图中的曲线就叫函数(x>0)
的图象.
例1、下图反映的过程是小明从家去食堂吃早餐,
接着去图书馆读报,然后回家.其中x
表示时间,y
表示小明离家的距离,小明家、食堂、图书馆在同一直线上.
根据图象回答下列问题:
(1)食堂离小明家多远?小明从家到食堂用了多少时间?
(2)小明在食堂吃早餐用了多少时间?
(3)食堂离图书馆多远?小明从食堂到图书馆用了多少时间?
(4)小明读报用了多长时间?
(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
四、随堂练习:书79页练习2题。
五、小结
六、布置作业
教学后记:
19.1.2函数的图象(2)
教学目标:
1.会用描点法画出函数图象,能说出画函数图象的步骤;
2.会判断一个点是否在函数的图象上;
3.能初步通过分析图象中变量的对应关系、变化规律和变化趋势,体会数形结合思想.
教学重点:描点法画出函数图象.
教学难点:理解解析法和图象法表示函数关系的相互转换.
教学过程:
一、预习检测:
(1)函数图象上的点的横纵坐标分别表示什么?
(2)用描点法画函数图象按照哪些步骤进行?
、
(3)怎样从图象上看出当自变量增大时,对应的函数值是增大还是减小?
3、
合作交流:
下列式子中,对于
x
每一个确定的值,y
有唯一的对应值,即
y
是
x
的函数,请画出这些函数的图象.
(1)y=x+0.5
;
列表:
x
…
-3
-2
-1
0
1
2
3
…
y=x+0.5
…
-2.5
-1.5
-0.5
0.5
1.5
2.5
3.5
…
(1)这个函数的自变量取值范围是什么?为什么表格中
-3
前和3
后还有一栏要写省略号?
(2)画出的图象是什么?图象上的点从左向右运动时,这个点是越来越高还是越来越低?能否用坐标解释这一图形特点?
(3)当自变量的值越来越大时,对应的函数值怎样变化?
三、释疑解惑:
归纳:由函数解析式画函数图象,一般按下列步骤进行:
1.列表:列表给出自变量与函数的一些对应值;
2.描点:以表中对应值为坐标,在坐标平面内描出相应的点;
3.连线:按照自变量由小到大的顺序,把所描各点用光滑的曲线连结起来.
描出的点越多,图象越精确.有时不能把所有的点都描出,就用光滑的曲线连结画出的点,从而得到函数的近似的图象.
例
画出函数
(x大于0)的图象.
四、随堂测评
(1)判断下列各点是否在函数y=x+0.5的图象上?
①(-4,-4.5);
②(4,4.5).
(2)判断下列各点是否在函数
的图象上?
1
(2,3);②(4,2).
(3)教科书P79练习第1、3
题.
五
、归纳小结
1、画函数图象的一般步骤:列表、描点、连线,这种
画函数图象的方法称为描点法.
2.如何从图象中了解函数的变化情况?
5、
布置作业
教学后记
19.1.2函数的图象(3)
教学目标:
1.了解函数的三种表示法及其优缺点;
2.能用适当的方式表示简单实际问题中的变量之间的函数关系;
3.能对函数关系进行分析,对变量的变化情况进行初步讨论.
教学重点:
综合运用三种表示法表示函数关系,研究运动变化过程.
教学难点:用适当的方式表示简单实际问题中的变量之间的函数关系;对函数关系进行分析,对变量的变化情况进行初步讨论
教学过程
一、
预习检测:
1、
什么是函数?2、函数关系有几种表示方法?
二、合作交流:
(1)对于每一个大于0
的自变量的值,想准确确定对应的函数值,用什么表示法较好?
(2)对于x
的值分别为1,2,3,4,5,6
时,想知
道其对应的函数值,用什么表示方法较好?
(3)想知道当x
的值增大时,函数值y
怎样变化,用什么表示方法较好?
三、释疑解惑:
例4、一水库的水位在最近5
h
内持续上涨,下表记录
了这5
h
内6
个时间点的水位高度,其中
t
表示时间,y表
示水位高度.
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么
规律?
(2)水位高度
y
是否为时间
t
的函数?如果是,试写出一个符合表中数据的函数解析式,并画出函数图象。这个函数能表示水位的变化规律吗?
(3)据估计这种上涨规律还会持续2
h,预测再过2
h水位高度将达到多少米.
四、随堂练习:书81页1、2、3
五、小结
(1)函数有哪几种表示方法?这些表示方法分别有哪些优势和不足?
(2)怎样根据函数分析变量的变化规律和变化趋势?
六、布置作业
教学后记
19.2一次函数
19.2.1正比例函数(1)
教学目标:
1.理解正比例函数的概念;
2.根据实际问题列出简单的正比例函数的表达式
教学重点:正比例函数的概念.
教学难点:理解正比例函数的概念,能正确用函数关系式表达实际问题
教学过程
一、预习检测:
什么是正比例函数?
二、合作交流:
问题1 2011年开始运营的京沪高速铁路全长1
318
km.设列车的平均速度为300
km/h.考虑以下问题:
(1)乘京沪高铁列车,从始发站北京南站到终点站上海虹桥站,约需多少小时(结果保留小数点后一位)?
(2)如果从小学学习过的比例观点看,列车在运行过程中,行程
y(单位:km)和运行时间
t(单位:h)是什么关系?
(3)如果从函数的观点看,京沪高铁列车的行程
y(单位:km)是运行时间
t(单位:h)的函数吗?能写出这个函数的解析式,并写出自变量的取值范围吗?
(4)乘京沪高铁列车从北京南站出发2.5
h后,是否已经过了距始发站1
100
km
的南京南站?
思考:(1)这个问题中得到的函数解析式有什么特点?
(2)函数值与对应的自变量的值的比有什么特点?
思考:下列问题中,变量之间的对应关系是函数关
系吗?如果是,请写出函数解析式.
(1)圆的周长
l
随半径
r
的变化而变化;
(2)铁的密度为7.8
g/cm3,铁块的质量
m(单位:g)随它的体积
V(单位:cm3)的变化而变化;
(3)每个练习本的厚度为0.5
cm,练习本摞在一起的总厚度
h(单位:cm)随练习本的本数
n
变化而变化;
(4)冷冻一个0
℃
的物体,使它每分下降2
℃,物体的温度
T(单位:℃)随冷冻时间
t(单位:min)的变化而变化.
三、释疑解惑
认真观察这四个函数解析式,说说这些函数有什么共同点.
归纳:正比例函数的定义:一般地,形如
y=kx(k
是常数,k≠0)的函数,叫做正比例函数,其中k
叫做比例系数.
四、随堂练习:书87页1、2题
五、小结
六、布置作业
教学后记
19.2.1正比例函数(2)
教学目标:
1、理解正比例函数图象特征。
2、知道正比例函数图象是直线,会画正比例函数的图象;进一步熟悉作函数图象的主要步骤。
教学重点: 探索正比例函数图形的形状,会画正比例函数图象
教学难点:正比例函数的图象性质特点的掌握。
教学过程
一、预习检测:
1、什么是正比例函数?
2、在下列函数中,哪些是正比例函数?并指出正比例系数分别是多少.
①y=x,
②y=3x2,
③
y=2x
,
④y=2x-4,
⑤
,
⑥y=-x
,
⑦y=-2x.
3、正比例函数的图象是什么形状?怎样画它的图象?
2、合作交流:
1、在同一坐标系中用描点法画出正比例函数
y
=2x和
的图象.
2、画出函数y
=-3x
和y
=-1.5x
的图象,
进行小组合作讨论:每组中这两个函数的图象形状是什么?位置怎样?有什么特征?
三、释疑解惑:
正比例函数的图象性质及特征:
1.正比例函数的图象都是经过原点的直线,一般选取画它的0,0)和(1,k)图象
2.在画函数图象时,使函数图象位置发生变化的量是k。
3.
性质
(1)当k>0时,y随x的增大而增大,直线经过一、三象限,从左到右是上升的;
2)当k<0时,y随x的增大而减小,直线经过二、四象限,从左到右是下降的.
四、随堂测评:
1.若正比例函数y=(k-3)x满足下列条件,求出k的范围
(1)y
随x的增大而增大;(2)图象经过一、三象限;
(3)图象如图所示.
2.已知
y关于x的正比例函数
y=(k+3)x|k|-4,且
y随x的增大而减小,那么k=________.
3、课本P90练习
五、归纳小结:正比例函数的图象是什么?有哪些性质?
六、布置作业:
教学后记:
19.2.2一次函数(1)
教学目标:
1.知道一次函数解析式的特点及意义,能结合实际
问题中的数量关系写出一次函数的解析式;
2.能辨别正比例函数与一次函数的区别与联系;
3.
初步体会用待定系数法求一次函数解析式的方法.
教学重点:一次函数的概念.
教学难点:一次函数与正比例函数的关系
教学过程:
一、预习检测
1、什么是正比例函数?正比例函数的图象性质与特征?
2、问题1 某登山队大本营所在地的气温为5
℃,海拔每升高1
km
气温下降6
℃.登山队员由大本营向上登高x
km
时,他们所处位置的气温是
y
℃.试用函数解析式表示
y
与
x
的关系.、
解:y=-6x+5;
二、
合作交流
问题2 下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式,这些函数解析式有哪些共同特征?
(1)有人发现,在20
℃~25
℃时蟋蟀每分鸣叫次数
c
与温度
t(单位:℃)有关,且
c
的值约是
t
的7
倍与35
的差;
(2)一种计算成年人标准体重G(单位:kg)的方法是,以厘米为单位量出身高值
h
,再减常数105,所得差是G
的值;
(3)某城市的市内电话的月收费额
y(单位:元)包括月租费22元和拨打电话
x
min
的计时费(按0.1元/min收取);
(4)把一个长10
cm,宽5
cm的矩形的长减少
x
cm,宽不变,矩形面积
y(单位:cm2)随x的值而变化.
(1)C=7t-35;(20≤t≤25)
(2)G=h-105;
(3)y=0.1x+22
(4)y=-5x+50.
(0≤x≤10)
观察以上出现的四个函数解析式,很显然它们不是正比例函数,那么它们在形式上有什么共同特征呢?
这些函数的形式都是自变量的k(常数)倍与一个常数的和。
3、
释疑解惑:
一次函数的定义:一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数。
当b=0时,y=kx+b就变成了y=kx,从中你有什么发现?
正比例函数式特殊的一次函数。
例1、
已知函数y=(k-2)x+2k+1,若它是正比例函数,求k的值.若它是一次函数,求k的值.
例2
已知y与x-3成正比例,当x=4时,y=3.
(1)写出y与x之间的函数关系式;
(2)y与x之间是什么函数关系;
(3)求x=2.5时,y的值.
4、
随堂练习:
课本90-91页练习
五、归纳总结
(1)什么叫一次函数?
(2)一次函数与正比例函数有什么联系?
六、布置作业
教学后记
19.2.2一次函数(2)
教学目标:
1、理解一次函数图象特征与解析式的联系规律;
2、会用简单方法画一次函数的图象,会求一次函数与坐标轴的交点坐标;
教学重点:一次函数图象特征与解析式联系规律;
一次函数图象的画法。
教学难点:一次函数图象特征与解析式联系规律
教学过程:
一、预习检测:
1.一次函数的图象是什么,如何简便地画出一次函数的图象?
(一次函数y=kx+b(k≠0)的图象是一条直线,画一次函数图象时,取两点即可画出函数的图象).
2.正比例函数y=kx(k≠0)的图象是经过哪一点的直线?
(正比例函数y=kx(k≠0)的图象是经过原点(0,0)的一条直线).
3.平面直角坐标系中,x轴、y轴上的点的坐标有什么特征?
二、合作交流
1、
画出函数
y
=
-6x与
y=-6x+5
的图象。
2、完成书91页思考
结论:一次函数y=kx+b的图象是一条直线,我们称它为直线y=kx+b,它可以看作由直线y=kx平移b绝对值个单位长度而得到(当b>0时,向上平移;当b< 0时,向下平移)。
三、释疑解惑
例3、画出函数y=2x-1与y=-0.5x+1的图象
解析:过(0,-1)点与(1,1)点画出直线y=2x-1.
过(0,1)点与(1,0.5)点画出直线y=-0.5x+1
结论:1、当k>0时,y随x的增大而增大,当k<0时,y随x的增大而减小
、
2、例
已知一次函数
y=(1-2m)x+m-1
,
求满足下列条件的m的值:
(1)函数值y
随x的增大而增大;(2)函数图象与y
轴的负半轴相交;
(3)函数的图象过第二、三、四象限;(4)函数的图象过原点。
四、随堂练习:课本93页练习
五、归纳总结:一次函数的图像与性质
六、布置作业
教学后记
19.2.2一次函数(3)
教学目标:
1.学会用待定系数法求一次函数解析式;
2.了解分段函数的表示及其图象;能初步应用一次函数模型解决现实生活中的问题。
的应用价值.
教学重点:
用待定系数法求一次函数解析式,初步了解分段函数
教学难点:应用一次函数解决实际问题。
教学过程:
一、预习检测
1、
正比例函数和一次函数的解析式;它们的关系怎样?图象与性质各是什么?
2、
什么是待定系数法?
二、合作交流
已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式.
三、精讲解惑:
像这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法.
例5 “黄金1号”玉米种子的价格为5
元/kg,如果
一次购买2
kg
以上的种子,超过2
kg
部分的种子的价格打8
折.
购买种子数量/kg
0.5
1
1.5
2
2.5
3
3.5
4
…
付款金额/元
…
(1)填出下表:
(2)写出付款金额
y(单位:元)与购买种子数量
x(单位:kg)之间的函数解析式,并画出函数图象.
四、随堂练习:书95页1、
五、归纳总结:如何用待定系数法求一次函数的解析式
六、布置作业:
教学后记:
19.2.3一次函数与方程、不等式(1)
教学目标:
1.使学生理解二元一次方程组的解是两条直线的交点坐标,并能通过图象法来求二元一次方程组的解;
2.让学生了解到函数是刻画和研究现实世界数量关系的重要数学模型,也是一种重要的数学思想,培养和提高学生在数学学习中的创造和应用函数的能力.
教学重点:使学生体会到二元一次方程组的解是两条直线的交点坐标,能通过图象法来求二元一次方程组的解.
教学难点:使学生体会到实际问题中数量之间的相互关系,学会用函数的思想去进行描述、研究其内在联系和变化规律;
教学过程
一、预习检测:
1、画出一次函数y=2x+1的图象,当函数值y=3、0、-1时,自变量x的值分别是多少?
2、解方程:(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
二、合作交流
下面三个方程有什么共同特点?你能从函数的角度对解这三个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
用函数的观点看:
解一元一次方程
ax
+b
=k
就是求当函数值为k
时对应的自变量的值.
三、精讲解惑:
从形的角度看,二元一次方程与一次函数有什么关系?
一般地,以方程
y
=kx+b(其中k,b
为常数,
k≠0)的解为坐标的点组成的图形与一次函数
y
=kx+b
的图象有什么关系?
例题:1号探测气球从海拔5
m
处出发,以1
m/min
的速度上升.与此同时,2
号探测气球从海拔15
m
处出发,以0.5
m/min
的速度上升.两个气球都上升了1
h.
(1)请用解析式分别表示两个气球所在位置的海拔
y(m)与气球上升时间
x(min)的函数关系.
气球1
海拔高度:y
=x+5;
气球2
海拔高度:y
=0.5x+15.
(2)在某时刻,两个气球能否位于同一高度?如果能,这时气球上升了多少时间?位于什么高度?
归纳:从形的角度看,二元一次方程组与一次函数有什么关系?
二元一次方程组的解就是相应的两个一次函数图象的交点坐标.
四、随堂练习:书98页练习
5、
归纳总结
6、
布置作业:
教学后记:
19.2.3一次函数与方程、不等式(2)
教学目标
1:理解一次函数与一元一次不等式的关系,会根据一次函数的图象解决一元一次不等式的求解问题.
2:学习用函数的观点看待不等式的方法,初步形成用全面的观点处理局部问题的思想
教学重点:使学生体会一次函数与不等式的关系,会根据一次函数的图象解决一元一次不等式的求解问题.
教学难点:使学生体会到实际问题中数量之间的相互关系,学会用函数的思想去进行描述、研究其内在联系和变化规律;
教学过程:
一、预习检测
二元一次方程与一次函数有什么关系?二元一次方程组呢?
2、合作交流:
下面三个不等式有什么共同特点?解不等式。
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
你能从函数的角度对解这三个不等式进行解释吗?能把你得到的结论推广到一般情形吗?
三、释疑解惑:
4、随堂测评;学习之友
5、归纳总结
6、布置作业
教学后记
第十九章一次函数
八
年
级
备
课
组
第十九章一次函数
19.1.1变量与函数(1)
教学目标
1.掌握常量和变量、自变量和函数的基本概念;
2.引导学生联系代数式和方程的相关知识,继续探索数量关系,增强数学建模意识,列出函数关系式.
教学重点:了解变量与常量的意义,充分体会运动变化过程中量的变化.
难点:能用解析法正确表示数量关系。
教学过程
1、
预习检测:
找出下面问题中变化的量和不变的量:
(1)汽车以60
km/h
的速度匀速行驶,行驶时间为
t
h,行驶路程为
s
km.
(2)每张电影票的售价为10
元,设某场电影售出x
张票,票房收入为y
元.
二、合作交流:
(1)圆形水波慢慢地扩大,在这一过程中,当圆的半径r
分别为10
cm,20
cm,30
cm
时,圆的面积S
分别为多少?在这个过程中,哪些量是变化的?
(2)用10
m长的绳子围一个矩形,当矩形的一边长x
分别为3
m,3.5
m,4
m,4.5
m
时,它的邻边长y
分别为多少?在矩形改变形状的变化过程中,哪些量是变化的?哪些量是固定不变的?
三、精讲解惑
1,常量和变量
上述运动变化过程中出现的数量,你认为可以怎样分类?
在上面的问题中,我们研究了一些数量关系,它们都刻画了某些变化规律.这里出现了各种各样的量,特别值得注意的是出现了一些数值会发生变化的量.例如问题1中,刻画气温变化规律的量是时间t和气温T,气温T随着时间t的变化而变化,它们都会取不同的数值.像这样在某一变化过程中,可以取不同数值的量,叫做变量(variable).问题的研究过程中,还有一种量,它的取值始终保持不变,我们称之为常量(constant)。
2
例1、
写出下列各问题中的关系式,并指出其中的常量与变量:
(1)圆的周长C与半径r的关系式;
(2)(2)火车以60千米/时的速度行驶,它驶过的路程s(千米)和所用时间t(时)的关系式;
(3)n边形的内角和S与边数n的关系式.
解
(1)C=2π
r,2π是常量,r、C是变量;
(2)s=60t,60是常量,t、s是变量;
(3)S=(n-2)×180,2、180是常量,n、S是变量.
4、
随堂练习:
1、指出下列变化过程中的变量和常量:
(1)
汽油的价格是7.4元/升,加油
x
L,车主加油
付油费
y
元;
(2)
小明看一本200
页的小说,看完这本小说需要
t
天,平均每天所看的页数为
n;
(3)
用长为40
cm
的绳子围矩形,围成的矩形一边
长为
x
cm,其面积为
S
cm2.
2、书71页练习
五、小结
在某个变化过程中,可以取不同数值的量,叫做变量;数值始终保持不变的量,叫做常量.例如x和y,对于x的每一个值,y都有惟一的值与之对应,我们就说x是自变量,y是因变量.
六、布置作业:
教学后记:
19.1.1变量与函数(2)
教学目标:
1.进一步体会运动变化过程中的数量变化;
2.从典型实例中抽象概括出函数的概念,了解函数的概念.
教学重点:概括并理解函数概念中的单值对应关系,用式子表示变量间的关系
教学难点:用含有一个变量的式子表示另一个变量
教学过程
一、预习检测:什么是变量?什么是常量?
二、合作交流:
问题1 下面变化过程中的变量之间有什么联系?
(1)汽车以60
km/h
的速度匀速行驶,行驶的时间为t
h,行驶的路程为s
km;
问题2 下面变化过程中的变量之间有什么联系?
(2)每张电影票的售价为10
元,设某场电影售出
x
张票,票房收入为
y
元;
(3)圆形水波慢慢地扩大,在这一过程中,圆的半径为
r
,面积为
S
;
(4)用10
m
长的绳子围一个矩形,当矩形的一边长为
x,它的邻边长为
y.
三
释疑解惑:
函数的定义:一般地,在一个变化过程中,如果有两个变量
x
与
y,并且对于
x
的每一个确定的值,y
都有唯一确定的值与其对应,那么我们就说
x
是自变量,y
是
x
的函数.如果当
x
=a
时,对应的
y
=b,那么
b
叫做当自变量的值为
a
时的函数值.
4、随堂练习:
课本P74页-75页练习
五、总结归纳:
1.函数概念包含:(1)两个变量;(2)两个变量之间的对应关系.
2.函数关系三种表示方法:(1)解析法;(2)列表法;(3)图象法.
六、布置作业
教学后记:
19.1.2函数的图象(1)
教学目标
1.了解函数图象的意义;
2.会观察函数图象获取信息,根据图象初步分析函
数的对应关系和变化规律;
3.经历画函数图象的过程,体会函数图象建立数形联系的关键是分别用点的横、纵坐标表示自变量和对应的函数值.
教学重点:函数图象的意义,从图象中获取信息.
难点:会观察函数图象获取信息,根据图象初步分析函
数的对应关系和变化规律;
教学过程
1、
预习检测:
下图是北京市某天24
小时内气温的变化图,气温
T
随时间
t的变化而变化.
你从图中得到哪些信息?
在9~14
时,T
随着t
的增大而增大,14~16
时,T
基本不变;16~次日5
时,T
的值随着t
的增大而减小;次日5~8
时,T
变化不大;
结论:图形能直观地反映出函数值怎样随自变量的变化而变化!
2、
合作交流:
请画出下面问题中能直观地反映函数变化规律的图形:
正方形面积
S
与边长
x
之间的函数解析式为
S=x2.
思考(1)怎样确定满足函数关系的点的坐标?
(2)取一些自变量的值,计算出相应的函数值.自变量x
的一个确定的值与它所对应的唯一
的函数值S,是否唯一确定了一个(x,S)呢?
(1)填写下表:
三、释疑解惑:
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.如右图中的曲线就叫函数(x>0)
的图象.
例1、下图反映的过程是小明从家去食堂吃早餐,
接着去图书馆读报,然后回家.其中x
表示时间,y
表示小明离家的距离,小明家、食堂、图书馆在同一直线上.
根据图象回答下列问题:
(1)食堂离小明家多远?小明从家到食堂用了多少时间?
(2)小明在食堂吃早餐用了多少时间?
(3)食堂离图书馆多远?小明从食堂到图书馆用了多少时间?
(4)小明读报用了多长时间?
(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
四、随堂练习:书79页练习2题。
五、小结
六、布置作业
教学后记:
19.1.2函数的图象(2)
教学目标:
1.会用描点法画出函数图象,能说出画函数图象的步骤;
2.会判断一个点是否在函数的图象上;
3.能初步通过分析图象中变量的对应关系、变化规律和变化趋势,体会数形结合思想.
教学重点:描点法画出函数图象.
教学难点:理解解析法和图象法表示函数关系的相互转换.
教学过程:
一、预习检测:
(1)函数图象上的点的横纵坐标分别表示什么?
(2)用描点法画函数图象按照哪些步骤进行?
、
(3)怎样从图象上看出当自变量增大时,对应的函数值是增大还是减小?
3、
合作交流:
下列式子中,对于
x
每一个确定的值,y
有唯一的对应值,即
y
是
x
的函数,请画出这些函数的图象.
(1)y=x+0.5
;
列表:
x
…
-3
-2
-1
0
1
2
3
…
y=x+0.5
…
-2.5
-1.5
-0.5
0.5
1.5
2.5
3.5
…
(1)这个函数的自变量取值范围是什么?为什么表格中
-3
前和3
后还有一栏要写省略号?
(2)画出的图象是什么?图象上的点从左向右运动时,这个点是越来越高还是越来越低?能否用坐标解释这一图形特点?
(3)当自变量的值越来越大时,对应的函数值怎样变化?
三、释疑解惑:
归纳:由函数解析式画函数图象,一般按下列步骤进行:
1.列表:列表给出自变量与函数的一些对应值;
2.描点:以表中对应值为坐标,在坐标平面内描出相应的点;
3.连线:按照自变量由小到大的顺序,把所描各点用光滑的曲线连结起来.
描出的点越多,图象越精确.有时不能把所有的点都描出,就用光滑的曲线连结画出的点,从而得到函数的近似的图象.
例
画出函数
(x大于0)的图象.
四、随堂测评
(1)判断下列各点是否在函数y=x+0.5的图象上?
①(-4,-4.5);
②(4,4.5).
(2)判断下列各点是否在函数
的图象上?
1
(2,3);②(4,2).
(3)教科书P79练习第1、3
题.
五
、归纳小结
1、画函数图象的一般步骤:列表、描点、连线,这种
画函数图象的方法称为描点法.
2.如何从图象中了解函数的变化情况?
5、
布置作业
教学后记
19.1.2函数的图象(3)
教学目标:
1.了解函数的三种表示法及其优缺点;
2.能用适当的方式表示简单实际问题中的变量之间的函数关系;
3.能对函数关系进行分析,对变量的变化情况进行初步讨论.
教学重点:
综合运用三种表示法表示函数关系,研究运动变化过程.
教学难点:用适当的方式表示简单实际问题中的变量之间的函数关系;对函数关系进行分析,对变量的变化情况进行初步讨论
教学过程
一、
预习检测:
1、
什么是函数?2、函数关系有几种表示方法?
二、合作交流:
(1)对于每一个大于0
的自变量的值,想准确确定对应的函数值,用什么表示法较好?
(2)对于x
的值分别为1,2,3,4,5,6
时,想知
道其对应的函数值,用什么表示方法较好?
(3)想知道当x
的值增大时,函数值y
怎样变化,用什么表示方法较好?
三、释疑解惑:
例4、一水库的水位在最近5
h
内持续上涨,下表记录
了这5
h
内6
个时间点的水位高度,其中
t
表示时间,y表
示水位高度.
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么
规律?
(2)水位高度
y
是否为时间
t
的函数?如果是,试写出一个符合表中数据的函数解析式,并画出函数图象。这个函数能表示水位的变化规律吗?
(3)据估计这种上涨规律还会持续2
h,预测再过2
h水位高度将达到多少米.
四、随堂练习:书81页1、2、3
五、小结
(1)函数有哪几种表示方法?这些表示方法分别有哪些优势和不足?
(2)怎样根据函数分析变量的变化规律和变化趋势?
六、布置作业
教学后记
19.2一次函数
19.2.1正比例函数(1)
教学目标:
1.理解正比例函数的概念;
2.根据实际问题列出简单的正比例函数的表达式
教学重点:正比例函数的概念.
教学难点:理解正比例函数的概念,能正确用函数关系式表达实际问题
教学过程
一、预习检测:
什么是正比例函数?
二、合作交流:
问题1 2011年开始运营的京沪高速铁路全长1
318
km.设列车的平均速度为300
km/h.考虑以下问题:
(1)乘京沪高铁列车,从始发站北京南站到终点站上海虹桥站,约需多少小时(结果保留小数点后一位)?
(2)如果从小学学习过的比例观点看,列车在运行过程中,行程
y(单位:km)和运行时间
t(单位:h)是什么关系?
(3)如果从函数的观点看,京沪高铁列车的行程
y(单位:km)是运行时间
t(单位:h)的函数吗?能写出这个函数的解析式,并写出自变量的取值范围吗?
(4)乘京沪高铁列车从北京南站出发2.5
h后,是否已经过了距始发站1
100
km
的南京南站?
思考:(1)这个问题中得到的函数解析式有什么特点?
(2)函数值与对应的自变量的值的比有什么特点?
思考:下列问题中,变量之间的对应关系是函数关
系吗?如果是,请写出函数解析式.
(1)圆的周长
l
随半径
r
的变化而变化;
(2)铁的密度为7.8
g/cm3,铁块的质量
m(单位:g)随它的体积
V(单位:cm3)的变化而变化;
(3)每个练习本的厚度为0.5
cm,练习本摞在一起的总厚度
h(单位:cm)随练习本的本数
n
变化而变化;
(4)冷冻一个0
℃
的物体,使它每分下降2
℃,物体的温度
T(单位:℃)随冷冻时间
t(单位:min)的变化而变化.
三、释疑解惑
认真观察这四个函数解析式,说说这些函数有什么共同点.
归纳:正比例函数的定义:一般地,形如
y=kx(k
是常数,k≠0)的函数,叫做正比例函数,其中k
叫做比例系数.
四、随堂练习:书87页1、2题
五、小结
六、布置作业
教学后记
19.2.1正比例函数(2)
教学目标:
1、理解正比例函数图象特征。
2、知道正比例函数图象是直线,会画正比例函数的图象;进一步熟悉作函数图象的主要步骤。
教学重点: 探索正比例函数图形的形状,会画正比例函数图象
教学难点:正比例函数的图象性质特点的掌握。
教学过程
一、预习检测:
1、什么是正比例函数?
2、在下列函数中,哪些是正比例函数?并指出正比例系数分别是多少.
①y=x,
②y=3x2,
③
y=2x
,
④y=2x-4,
⑤
,
⑥y=-x
,
⑦y=-2x.
3、正比例函数的图象是什么形状?怎样画它的图象?
2、合作交流:
1、在同一坐标系中用描点法画出正比例函数
y
=2x和
的图象.
2、画出函数y
=-3x
和y
=-1.5x
的图象,
进行小组合作讨论:每组中这两个函数的图象形状是什么?位置怎样?有什么特征?
三、释疑解惑:
正比例函数的图象性质及特征:
1.正比例函数的图象都是经过原点的直线,一般选取画它的0,0)和(1,k)图象
2.在画函数图象时,使函数图象位置发生变化的量是k。
3.
性质
(1)当k>0时,y随x的增大而增大,直线经过一、三象限,从左到右是上升的;
2)当k<0时,y随x的增大而减小,直线经过二、四象限,从左到右是下降的.
四、随堂测评:
1.若正比例函数y=(k-3)x满足下列条件,求出k的范围
(1)y
随x的增大而增大;(2)图象经过一、三象限;
(3)图象如图所示.
2.已知
y关于x的正比例函数
y=(k+3)x|k|-4,且
y随x的增大而减小,那么k=________.
3、课本P90练习
五、归纳小结:正比例函数的图象是什么?有哪些性质?
六、布置作业:
教学后记:
19.2.2一次函数(1)
教学目标:
1.知道一次函数解析式的特点及意义,能结合实际
问题中的数量关系写出一次函数的解析式;
2.能辨别正比例函数与一次函数的区别与联系;
3.
初步体会用待定系数法求一次函数解析式的方法.
教学重点:一次函数的概念.
教学难点:一次函数与正比例函数的关系
教学过程:
一、预习检测
1、什么是正比例函数?正比例函数的图象性质与特征?
2、问题1 某登山队大本营所在地的气温为5
℃,海拔每升高1
km
气温下降6
℃.登山队员由大本营向上登高x
km
时,他们所处位置的气温是
y
℃.试用函数解析式表示
y
与
x
的关系.、
解:y=-6x+5;
二、
合作交流
问题2 下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式,这些函数解析式有哪些共同特征?
(1)有人发现,在20
℃~25
℃时蟋蟀每分鸣叫次数
c
与温度
t(单位:℃)有关,且
c
的值约是
t
的7
倍与35
的差;
(2)一种计算成年人标准体重G(单位:kg)的方法是,以厘米为单位量出身高值
h
,再减常数105,所得差是G
的值;
(3)某城市的市内电话的月收费额
y(单位:元)包括月租费22元和拨打电话
x
min
的计时费(按0.1元/min收取);
(4)把一个长10
cm,宽5
cm的矩形的长减少
x
cm,宽不变,矩形面积
y(单位:cm2)随x的值而变化.
(1)C=7t-35;(20≤t≤25)
(2)G=h-105;
(3)y=0.1x+22
(4)y=-5x+50.
(0≤x≤10)
观察以上出现的四个函数解析式,很显然它们不是正比例函数,那么它们在形式上有什么共同特征呢?
这些函数的形式都是自变量的k(常数)倍与一个常数的和。
3、
释疑解惑:
一次函数的定义:一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数。
当b=0时,y=kx+b就变成了y=kx,从中你有什么发现?
正比例函数式特殊的一次函数。
例1、
已知函数y=(k-2)x+2k+1,若它是正比例函数,求k的值.若它是一次函数,求k的值.
例2
已知y与x-3成正比例,当x=4时,y=3.
(1)写出y与x之间的函数关系式;
(2)y与x之间是什么函数关系;
(3)求x=2.5时,y的值.
4、
随堂练习:
课本90-91页练习
五、归纳总结
(1)什么叫一次函数?
(2)一次函数与正比例函数有什么联系?
六、布置作业
教学后记
19.2.2一次函数(2)
教学目标:
1、理解一次函数图象特征与解析式的联系规律;
2、会用简单方法画一次函数的图象,会求一次函数与坐标轴的交点坐标;
教学重点:一次函数图象特征与解析式联系规律;
一次函数图象的画法。
教学难点:一次函数图象特征与解析式联系规律
教学过程:
一、预习检测:
1.一次函数的图象是什么,如何简便地画出一次函数的图象?
(一次函数y=kx+b(k≠0)的图象是一条直线,画一次函数图象时,取两点即可画出函数的图象).
2.正比例函数y=kx(k≠0)的图象是经过哪一点的直线?
(正比例函数y=kx(k≠0)的图象是经过原点(0,0)的一条直线).
3.平面直角坐标系中,x轴、y轴上的点的坐标有什么特征?
二、合作交流
1、
画出函数
y
=
-6x与
y=-6x+5
的图象。
2、完成书91页思考
结论:一次函数y=kx+b的图象是一条直线,我们称它为直线y=kx+b,它可以看作由直线y=kx平移b绝对值个单位长度而得到(当b>0时,向上平移;当b< 0时,向下平移)。
三、释疑解惑
例3、画出函数y=2x-1与y=-0.5x+1的图象
解析:过(0,-1)点与(1,1)点画出直线y=2x-1.
过(0,1)点与(1,0.5)点画出直线y=-0.5x+1
结论:1、当k>0时,y随x的增大而增大,当k<0时,y随x的增大而减小
、
2、例
已知一次函数
y=(1-2m)x+m-1
,
求满足下列条件的m的值:
(1)函数值y
随x的增大而增大;(2)函数图象与y
轴的负半轴相交;
(3)函数的图象过第二、三、四象限;(4)函数的图象过原点。
四、随堂练习:课本93页练习
五、归纳总结:一次函数的图像与性质
六、布置作业
教学后记
19.2.2一次函数(3)
教学目标:
1.学会用待定系数法求一次函数解析式;
2.了解分段函数的表示及其图象;能初步应用一次函数模型解决现实生活中的问题。
的应用价值.
教学重点:
用待定系数法求一次函数解析式,初步了解分段函数
教学难点:应用一次函数解决实际问题。
教学过程:
一、预习检测
1、
正比例函数和一次函数的解析式;它们的关系怎样?图象与性质各是什么?
2、
什么是待定系数法?
二、合作交流
已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式.
三、精讲解惑:
像这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法.
例5 “黄金1号”玉米种子的价格为5
元/kg,如果
一次购买2
kg
以上的种子,超过2
kg
部分的种子的价格打8
折.
购买种子数量/kg
0.5
1
1.5
2
2.5
3
3.5
4
…
付款金额/元
…
(1)填出下表:
(2)写出付款金额
y(单位:元)与购买种子数量
x(单位:kg)之间的函数解析式,并画出函数图象.
四、随堂练习:书95页1、
五、归纳总结:如何用待定系数法求一次函数的解析式
六、布置作业:
教学后记:
19.2.3一次函数与方程、不等式(1)
教学目标:
1.使学生理解二元一次方程组的解是两条直线的交点坐标,并能通过图象法来求二元一次方程组的解;
2.让学生了解到函数是刻画和研究现实世界数量关系的重要数学模型,也是一种重要的数学思想,培养和提高学生在数学学习中的创造和应用函数的能力.
教学重点:使学生体会到二元一次方程组的解是两条直线的交点坐标,能通过图象法来求二元一次方程组的解.
教学难点:使学生体会到实际问题中数量之间的相互关系,学会用函数的思想去进行描述、研究其内在联系和变化规律;
教学过程
一、预习检测:
1、画出一次函数y=2x+1的图象,当函数值y=3、0、-1时,自变量x的值分别是多少?
2、解方程:(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
二、合作交流
下面三个方程有什么共同特点?你能从函数的角度对解这三个方程进行解释吗?
(1)2x+1=3;(2)2x+1=0;(3)2x+1=-1.
用函数的观点看:
解一元一次方程
ax
+b
=k
就是求当函数值为k
时对应的自变量的值.
三、精讲解惑:
从形的角度看,二元一次方程与一次函数有什么关系?
一般地,以方程
y
=kx+b(其中k,b
为常数,
k≠0)的解为坐标的点组成的图形与一次函数
y
=kx+b
的图象有什么关系?
例题:1号探测气球从海拔5
m
处出发,以1
m/min
的速度上升.与此同时,2
号探测气球从海拔15
m
处出发,以0.5
m/min
的速度上升.两个气球都上升了1
h.
(1)请用解析式分别表示两个气球所在位置的海拔
y(m)与气球上升时间
x(min)的函数关系.
气球1
海拔高度:y
=x+5;
气球2
海拔高度:y
=0.5x+15.
(2)在某时刻,两个气球能否位于同一高度?如果能,这时气球上升了多少时间?位于什么高度?
归纳:从形的角度看,二元一次方程组与一次函数有什么关系?
二元一次方程组的解就是相应的两个一次函数图象的交点坐标.
四、随堂练习:书98页练习
5、
归纳总结
6、
布置作业:
教学后记:
19.2.3一次函数与方程、不等式(2)
教学目标
1:理解一次函数与一元一次不等式的关系,会根据一次函数的图象解决一元一次不等式的求解问题.
2:学习用函数的观点看待不等式的方法,初步形成用全面的观点处理局部问题的思想
教学重点:使学生体会一次函数与不等式的关系,会根据一次函数的图象解决一元一次不等式的求解问题.
教学难点:使学生体会到实际问题中数量之间的相互关系,学会用函数的思想去进行描述、研究其内在联系和变化规律;
教学过程:
一、预习检测
二元一次方程与一次函数有什么关系?二元一次方程组呢?
2、合作交流:
下面三个不等式有什么共同特点?解不等式。
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
你能从函数的角度对解这三个不等式进行解释吗?能把你得到的结论推广到一般情形吗?
三、释疑解惑:
4、随堂测评;学习之友
5、归纳总结
6、布置作业
教学后记
