高一物理人教版必修2课件:5.6 向心力 2 30 张PPT
文档属性
| 名称 | 高一物理人教版必修2课件:5.6 向心力 2 30 张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-07 07:18:09 | ||
图片预览






文档简介
(共30张PPT)
第五章
曲线运动
第六节
向心力
人教版必修2
1、做匀速圆周运动的物体一定有加速度吗?为什么?
2、做匀速圆周运动的物体的加速度有什么特点?写出向心加速度的公式。
3、做圆周运动的物体一定受力吗?
思考:
做圆周运动的物体的受力有什么特点?
受力的方向和大小如何确定?
水平光滑平面
小球在水平面内做匀速圆周运动
小球在水平面内做匀速圆周运动
小球在水平面内做匀速圆周运动
小球在水平面内做匀速圆周运动
小球在水平面内做匀速圆周运动
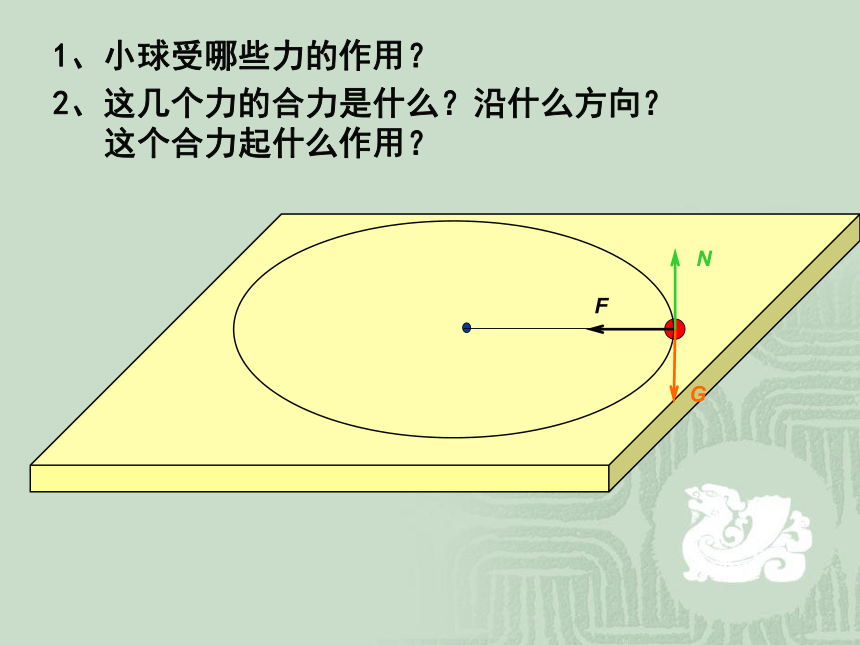
N
G
F
1、小球受哪些力的作用?
2、这几个力的合力是什么?沿什么方向?
这个合力起什么作用?
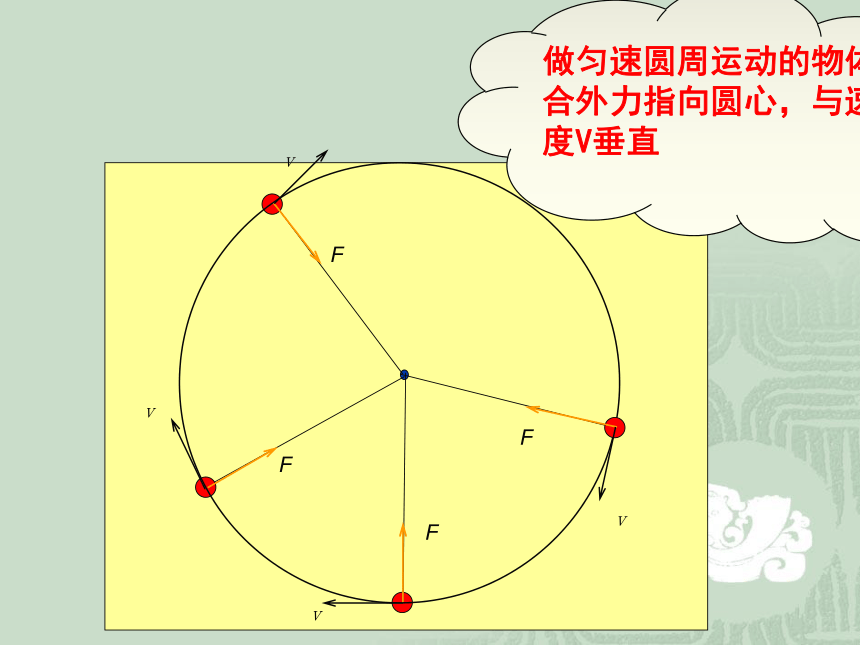
v
F
v
F
v
F
F
v
做匀速圆周运动的物体,合外力指向圆心,与速度V垂直
2、方向:总指向圆心,与速度垂直,方向不断变化。
3、效果:只改变速度方向,不改变速度大小。
一、向心力
1、定义:做匀速圆周运动的物体一定受到一个指向圆心的合力,这个力叫做向心力。
注意:
1、向心力是根据效果命名的力,并不是一种新的性质的力。
2、向心力的来源:可以是重力、弹力、摩擦力等各种性质的力,也可以是几个力的合力,还可以是某个力的分力。
G
Ff
FN
G
T
F
θ
总结
分析向心力来源的思路
明确研究对象
确定圆周运动所在的平面,明确圆周运动的轨迹、半径及圆心位置
进行受力分析,分析指向圆心方向的合力即向心力。
向心力的大小与
哪些物理量有关呢?
探究向心力的大小:
1、提出问题:向心力的大小与哪些因素有关?
2、猜想假设:
Fn与m、r、ω有关
3、设计实验:
4、进行实验:
控制变量法
保持r、m一定
Fn与ω的关系
保持m、ω一定
Fn与r的关系
保持r、ω一定
Fn与m的关系
5、得出结论:
保持r、m一定
Fn
∝ω2
保持m、ω一定
Fn∝
r
保持r、ω一定
Fn
∝m
Fn
=kmω2r
向心力演示器
1、公式:
Fn
=
mrω2
二、向心力的大小
=
mv2/r
=
mr(2π/T)2
2、单位:
m-kg
r-m
ω-rad/s
v-m/s
T-s
Fn-N
匀速圆周运动的受力特点:
方向始终指向圆心,不断改变
大小保持不变
三、变速圆周运动和一般曲线运动
1、变速圆周运动的合外力也指向圆心吗?
变速圆周运动的速度大小是怎么改变的?
2、怎么分析研究一般的曲线运动?
1、做变速圆周运动的物体所受的力
F
Fn
Ft
Ft
切向分力,它产生切向加速度,改变速度的大小.
Fn
向心分力,它产生向心加速度,改变速度的方向.
加速
2、处理一般曲线运动的方法:
把一般曲线分割为许多极短的小段,每一段都可以看作一小段圆弧.这些圆弧的弯曲程度不一样,表明它们具有不同的曲率半径.注意到这点区别之后,在分析质点经过曲线上某位置的运动时,就可以采用圆周运动的分析方法进行处理了.
r1
r2
知识小结
向心力
方向
大小
效果
来源
注意:匀速圆周运动和非匀速圆周运动的区别和联系。
方法总结
学会分析向心力的来源
学会利用向心力公式解决圆周运动问题
一般曲线运动的研究方法。
例题、把一个小球放在漏斗中,晃动漏斗,可以使小球沿光滑的漏斗壁在某一平面内做匀速圆周运动,如图,小球的向心力是什么力提供的?
课堂练习
解析:小球受力分析如图。
G
F
可见,向心力是重力G和支持力F的合力提供的.也可以认为是支持力F在水平方向的分力提供的
上题中,若小球转动的角速度为ω,如图倾角为α,试求小球做圆周运动的半径。
解析:小球受力分析如图。
mg
F
可知小球做圆周运动的向心力Fn为是重力G和支持力F的合力,有:
Fn=mg
tanα
=
mrω2
解得:r
=
g
tanα/ω2
α
第五章
曲线运动
第六节
向心力
人教版必修2
1、做匀速圆周运动的物体一定有加速度吗?为什么?
2、做匀速圆周运动的物体的加速度有什么特点?写出向心加速度的公式。
3、做圆周运动的物体一定受力吗?
思考:
做圆周运动的物体的受力有什么特点?
受力的方向和大小如何确定?
水平光滑平面
小球在水平面内做匀速圆周运动
小球在水平面内做匀速圆周运动
小球在水平面内做匀速圆周运动
小球在水平面内做匀速圆周运动
小球在水平面内做匀速圆周运动
N
G
F
1、小球受哪些力的作用?
2、这几个力的合力是什么?沿什么方向?
这个合力起什么作用?
v
F
v
F
v
F
F
v
做匀速圆周运动的物体,合外力指向圆心,与速度V垂直
2、方向:总指向圆心,与速度垂直,方向不断变化。
3、效果:只改变速度方向,不改变速度大小。
一、向心力
1、定义:做匀速圆周运动的物体一定受到一个指向圆心的合力,这个力叫做向心力。
注意:
1、向心力是根据效果命名的力,并不是一种新的性质的力。
2、向心力的来源:可以是重力、弹力、摩擦力等各种性质的力,也可以是几个力的合力,还可以是某个力的分力。
G
Ff
FN
G
T
F
θ
总结
分析向心力来源的思路
明确研究对象
确定圆周运动所在的平面,明确圆周运动的轨迹、半径及圆心位置
进行受力分析,分析指向圆心方向的合力即向心力。
向心力的大小与
哪些物理量有关呢?
探究向心力的大小:
1、提出问题:向心力的大小与哪些因素有关?
2、猜想假设:
Fn与m、r、ω有关
3、设计实验:
4、进行实验:
控制变量法
保持r、m一定
Fn与ω的关系
保持m、ω一定
Fn与r的关系
保持r、ω一定
Fn与m的关系
5、得出结论:
保持r、m一定
Fn
∝ω2
保持m、ω一定
Fn∝
r
保持r、ω一定
Fn
∝m
Fn
=kmω2r
向心力演示器
1、公式:
Fn
=
mrω2
二、向心力的大小
=
mv2/r
=
mr(2π/T)2
2、单位:
m-kg
r-m
ω-rad/s
v-m/s
T-s
Fn-N
匀速圆周运动的受力特点:
方向始终指向圆心,不断改变
大小保持不变
三、变速圆周运动和一般曲线运动
1、变速圆周运动的合外力也指向圆心吗?
变速圆周运动的速度大小是怎么改变的?
2、怎么分析研究一般的曲线运动?
1、做变速圆周运动的物体所受的力
F
Fn
Ft
Ft
切向分力,它产生切向加速度,改变速度的大小.
Fn
向心分力,它产生向心加速度,改变速度的方向.
加速
2、处理一般曲线运动的方法:
把一般曲线分割为许多极短的小段,每一段都可以看作一小段圆弧.这些圆弧的弯曲程度不一样,表明它们具有不同的曲率半径.注意到这点区别之后,在分析质点经过曲线上某位置的运动时,就可以采用圆周运动的分析方法进行处理了.
r1
r2
知识小结
向心力
方向
大小
效果
来源
注意:匀速圆周运动和非匀速圆周运动的区别和联系。
方法总结
学会分析向心力的来源
学会利用向心力公式解决圆周运动问题
一般曲线运动的研究方法。
例题、把一个小球放在漏斗中,晃动漏斗,可以使小球沿光滑的漏斗壁在某一平面内做匀速圆周运动,如图,小球的向心力是什么力提供的?
课堂练习
解析:小球受力分析如图。
G
F
可见,向心力是重力G和支持力F的合力提供的.也可以认为是支持力F在水平方向的分力提供的
上题中,若小球转动的角速度为ω,如图倾角为α,试求小球做圆周运动的半径。
解析:小球受力分析如图。
mg
F
可知小球做圆周运动的向心力Fn为是重力G和支持力F的合力,有:
Fn=mg
tanα
=
mrω2
解得:r
=
g
tanα/ω2
α
