北师版八年级下册6.4多边形的内角和与外角和 (2)数学课件(23张ppt)
文档属性
| 名称 | 北师版八年级下册6.4多边形的内角和与外角和 (2)数学课件(23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 22.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-08 06:46:02 | ||
图片预览





文档简介
(共23张PPT)
第六章平行四边形
6.4.2多边形的内角和与外角和
学习目标:
巩固提升
学习目标
情境导入
讲授新课
归纳总结
当堂检测
课后作业
1.了解多边形的外角定义,并能准确找出多边形的外角.
2.掌握多边形的外角和公式,利用内角和与外角和公式解决实际问题.
巩固提升
学习目标
复习回顾
讲授新课
归纳总结
当堂检测
课后作业
温故知新
1.从n边形的一个顶点出发可以引 条对角线,
它们把n边形分成 个三角形。
2.从一个n边形的一个顶点出发可以引5条对角线,则n= . =
3.多边形的内角和公式: .
4.正八边形的每一个内角为: .
(n-3)
(n-2)
8
(n-2)×180°
135°
复习回顾
巩固提升
学习目标
情景导入
归纳总结
当堂检测
课后作业
苏炳添为亚洲9秒关口第一人,是继刘翔之后中国田径赛场上的新纪录.
情境导入
巩固提升
学习目标
讲授新课
归纳总结
当堂检测
课后作业
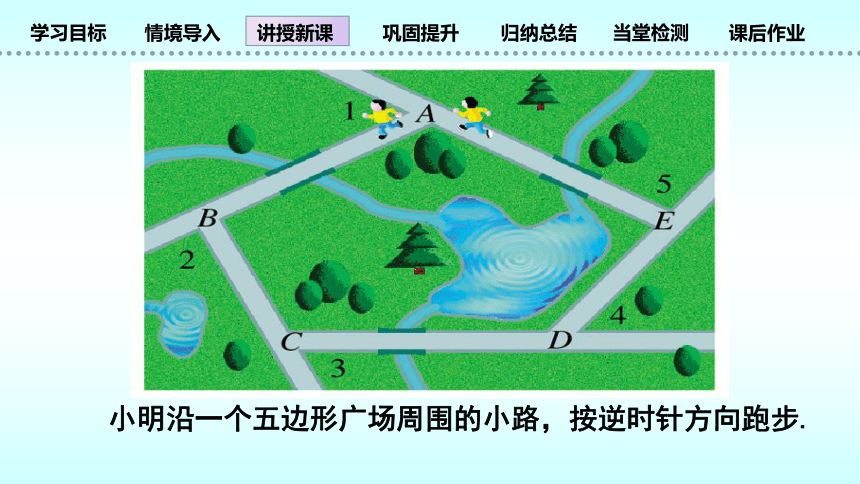
小明沿一个五边形广场周围的小路,按逆时针方向跑步.
情境导入
巩固提升
学习目标
讲授新课
归纳总结
当堂检测
课后作业
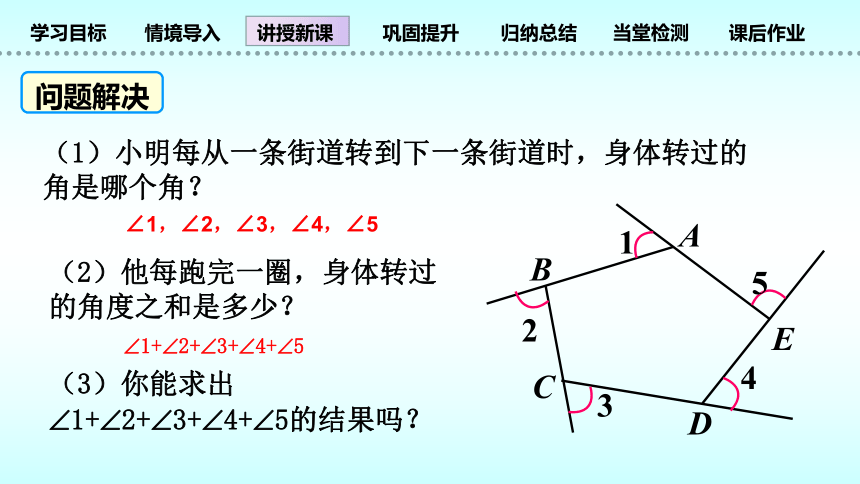
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?
问题解决
E
B
C
D
1
2
3
4
5
A
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)你能求出?1+?2+?3+?4+?5的结果吗?
∠1,∠2,∠3,∠4,∠5
?1+?2+?3+?4+?5
情境导入
巩固提升
学习目标
讲授新课
归纳总结
当堂检测
课后作业
集思广益
情境导入
巩固提升
学习目标
讲授新课
归纳总结
当堂检测
课后作业
集思广益
情境导入
巩固提升
学习目标
讲授新课
归纳总结
当堂检测
课后作业
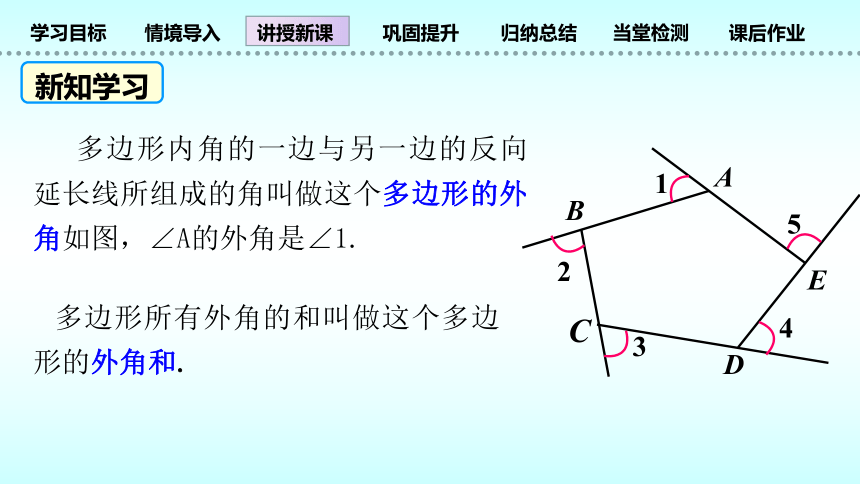
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角如图,∠A的外角是∠1.
多边形所有外角的和叫做这个多边形的外角和.
E
B
C
D
1
2
3
4
5
A
新知学习
情境导入
巩固提升
学习目标
讲授新课
归纳总结
当堂检测
课后作业
实践探究
猜想
n边形的外角和等于360°
360°
360°
360°
360°
由特殊到一般
情境导入
巩固提升
学习目标
讲授新课
归纳总结
当堂检测
课后作业
方法二:理论证明
因为n边形的每个外角与它相邻的内角互补
所以n个外角与n个内角的和是: n×180°
而n边形的内角和是: (n-2)×180°
所以n边形外角和是:
n×180°-(n-2) ×180°=360°.
与边数无关
结论
n边形的外角和等于360°
巩固提升
学习目标
情境导入
讲授新课
归纳总结
当堂检测
课后作业
应用举例
例1 一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,则它的内角和为
(n-2)·180°,外角和为360°.
则根据题意,
得(n-2)·180°=3×360°
解得n=8
所以这个多边形是八边形.
点播:已知内角和与外角和的关系求边数,往往利用方程求解.
已知内角和与外角和的关系求边数
建模思想
巩固提升
学习目标
情境导入
讲授新课
归纳总结
当堂检测
课后作业
变式训练
1.一个正多边形,它的一个外角等于与它相邻的内角的 ,
则这个多边形是( )
A.正十二边形 B.正十边形 C.正八边形 D.正六边形
解:设外角为x°,
由题意得,x=0.25(180°﹣x),
解得 x=36
360°÷36°=10,
所以,这个多边形是正十边形.
故选:B.
B
巩固提升
学习目标
情境导入
讲授新课
归纳总结
当堂检测
课后作业
应用举例
例2 一个正多边形每个外角都是60°,求这个多边形的边数?如果每个内角都是60°呢?
已知内外角求边数
∵每个外角都是60°,
∴360°÷60°=6
即这个多边形的边数是6.
∵每个内角都是60°,
∴每个外角=180°-60°=120°
∴360°÷120°=3
即这个多边形的边数是3.
点播:正多边形各内角都相等,因此各外角也都相等.求正多边形边数,可利用外角和360°,用外角和除以一个外角的度数即可求出边数.
转化思想
巩固提升
学习目标
情境导入
讲授新课
归纳总结
当堂检测
课后作业
变式训练
若一个正多边形的一个内角等于135°,
那么这个多边形是正 边形.
解:∵内角与外角互为邻补角,
∴正多边形的一个外角是180°﹣135°=45°,
∵多边形外角和为360°,
∴360°÷45°=8,
则这个多边形是正八边形.
八
巩固提升
学习目标
情境导入
讲授新课
归纳总结
当堂检测
课后作业
应用举例
例3.如图所示,在四边形ABCD中,AD⊥AB,∠C=110°,它的一个外角∠ADE=60°,则∠B的大小是 .?
利用多边形内外角关系求角的度数
解:∵∠ADE=60°,
∴∠ADC=120°,
∵AD⊥AB,
∴∠DAB=90°,
∴∠B=360°﹣∠C﹣∠ADC﹣∠A=40°。
40°
巩固提升
学习目标
情境导入
讲授新课
归纳总结
当堂检测
课后作业
应用举例
例4.如图所示,小丽从点A出发,沿直线前进10米后左转 24°再沿直线前进10米,又向左转24°……照这样走下去,她第一次回到出发地点A时,一共走的路程是 ( )
A.140米 B.150米 C.160米 D.240米
与多边形内角和及外角和有关的实际应用
解:∵多边形的外角和为360°,
而每一个外角为24°,
∴多边形的边数为360°÷24°=15,
∴小丽一共走了:15×10=150米.
B
巩固提升
学习目标
情境导入
例题讲解
归纳总结
当堂检测
课后作业
1.多边形的外角及外角和的定义;
2.多边形的外角和等于360°;
3.在探求过程中我们使用了观察、归纳的数学方法,并且运用了建模、转化等数学思想.
大家一起来
课堂小结
归纳总结
巩固提升
学习目标
情境导入
例题讲解
当堂检测
课后作业
1.一个多边形的每个内角均为108°,则这个多边形是( )
A.七边形 B.六边形 C.五边形 D.四边形
2.一个多边形的内角和与外角和之比是11∶2,那么这个多边形的边数是( )
A.13 B.12 C.11 D.10
3.正十二边形的每个内角都是 度.
4.一个多边形的内角和是外角和的4倍,则这个多边形是 边形.?
5.一个正多边形,它的一个外角等于与它相邻的内角的 ,
则这个多边形是正 边形.
C
A
十
八
150
归纳总结
巩固提升
学习目标
情境导入
例题讲解
当堂检测
课后作业
6.将两张三角形纸片如图6-4-17摆放,量得
∠1+∠2+∠3+∠4=220°,则∠5= .?
挑战自我
解: ∠1+∠2+∠6=180°,
∠3+∠4+∠7=180°,
∵∠1+∠2+∠3+∠4=220°,
∴∠1+∠2+∠6+∠3+∠4+∠7=360°,
∴∠6+∠7=140°,
∴∠5=180°﹣(∠6+∠7)=40°.
40°
当堂检测
请同学们完成
课本157页习题6.8 T1-T5。
归纳总结
巩固提升
学习目标
情境导入
例题讲解
课后作业
学习改变不了你生命的起点,
但一定能改变你生命的终点。
前路浩浩荡荡,万物皆可期。
同学们,加油!
谢谢
第六章平行四边形
6.4.2多边形的内角和与外角和
学习目标:
巩固提升
学习目标
情境导入
讲授新课
归纳总结
当堂检测
课后作业
1.了解多边形的外角定义,并能准确找出多边形的外角.
2.掌握多边形的外角和公式,利用内角和与外角和公式解决实际问题.
巩固提升
学习目标
复习回顾
讲授新课
归纳总结
当堂检测
课后作业
温故知新
1.从n边形的一个顶点出发可以引 条对角线,
它们把n边形分成 个三角形。
2.从一个n边形的一个顶点出发可以引5条对角线,则n= . =
3.多边形的内角和公式: .
4.正八边形的每一个内角为: .
(n-3)
(n-2)
8
(n-2)×180°
135°
复习回顾
巩固提升
学习目标
情景导入
归纳总结
当堂检测
课后作业
苏炳添为亚洲9秒关口第一人,是继刘翔之后中国田径赛场上的新纪录.
情境导入
巩固提升
学习目标
讲授新课
归纳总结
当堂检测
课后作业
小明沿一个五边形广场周围的小路,按逆时针方向跑步.
情境导入
巩固提升
学习目标
讲授新课
归纳总结
当堂检测
课后作业
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?
问题解决
E
B
C
D
1
2
3
4
5
A
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)你能求出?1+?2+?3+?4+?5的结果吗?
∠1,∠2,∠3,∠4,∠5
?1+?2+?3+?4+?5
情境导入
巩固提升
学习目标
讲授新课
归纳总结
当堂检测
课后作业
集思广益
情境导入
巩固提升
学习目标
讲授新课
归纳总结
当堂检测
课后作业
集思广益
情境导入
巩固提升
学习目标
讲授新课
归纳总结
当堂检测
课后作业
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角如图,∠A的外角是∠1.
多边形所有外角的和叫做这个多边形的外角和.
E
B
C
D
1
2
3
4
5
A
新知学习
情境导入
巩固提升
学习目标
讲授新课
归纳总结
当堂检测
课后作业
实践探究
猜想
n边形的外角和等于360°
360°
360°
360°
360°
由特殊到一般
情境导入
巩固提升
学习目标
讲授新课
归纳总结
当堂检测
课后作业
方法二:理论证明
因为n边形的每个外角与它相邻的内角互补
所以n个外角与n个内角的和是: n×180°
而n边形的内角和是: (n-2)×180°
所以n边形外角和是:
n×180°-(n-2) ×180°=360°.
与边数无关
结论
n边形的外角和等于360°
巩固提升
学习目标
情境导入
讲授新课
归纳总结
当堂检测
课后作业
应用举例
例1 一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,则它的内角和为
(n-2)·180°,外角和为360°.
则根据题意,
得(n-2)·180°=3×360°
解得n=8
所以这个多边形是八边形.
点播:已知内角和与外角和的关系求边数,往往利用方程求解.
已知内角和与外角和的关系求边数
建模思想
巩固提升
学习目标
情境导入
讲授新课
归纳总结
当堂检测
课后作业
变式训练
1.一个正多边形,它的一个外角等于与它相邻的内角的 ,
则这个多边形是( )
A.正十二边形 B.正十边形 C.正八边形 D.正六边形
解:设外角为x°,
由题意得,x=0.25(180°﹣x),
解得 x=36
360°÷36°=10,
所以,这个多边形是正十边形.
故选:B.
B
巩固提升
学习目标
情境导入
讲授新课
归纳总结
当堂检测
课后作业
应用举例
例2 一个正多边形每个外角都是60°,求这个多边形的边数?如果每个内角都是60°呢?
已知内外角求边数
∵每个外角都是60°,
∴360°÷60°=6
即这个多边形的边数是6.
∵每个内角都是60°,
∴每个外角=180°-60°=120°
∴360°÷120°=3
即这个多边形的边数是3.
点播:正多边形各内角都相等,因此各外角也都相等.求正多边形边数,可利用外角和360°,用外角和除以一个外角的度数即可求出边数.
转化思想
巩固提升
学习目标
情境导入
讲授新课
归纳总结
当堂检测
课后作业
变式训练
若一个正多边形的一个内角等于135°,
那么这个多边形是正 边形.
解:∵内角与外角互为邻补角,
∴正多边形的一个外角是180°﹣135°=45°,
∵多边形外角和为360°,
∴360°÷45°=8,
则这个多边形是正八边形.
八
巩固提升
学习目标
情境导入
讲授新课
归纳总结
当堂检测
课后作业
应用举例
例3.如图所示,在四边形ABCD中,AD⊥AB,∠C=110°,它的一个外角∠ADE=60°,则∠B的大小是 .?
利用多边形内外角关系求角的度数
解:∵∠ADE=60°,
∴∠ADC=120°,
∵AD⊥AB,
∴∠DAB=90°,
∴∠B=360°﹣∠C﹣∠ADC﹣∠A=40°。
40°
巩固提升
学习目标
情境导入
讲授新课
归纳总结
当堂检测
课后作业
应用举例
例4.如图所示,小丽从点A出发,沿直线前进10米后左转 24°再沿直线前进10米,又向左转24°……照这样走下去,她第一次回到出发地点A时,一共走的路程是 ( )
A.140米 B.150米 C.160米 D.240米
与多边形内角和及外角和有关的实际应用
解:∵多边形的外角和为360°,
而每一个外角为24°,
∴多边形的边数为360°÷24°=15,
∴小丽一共走了:15×10=150米.
B
巩固提升
学习目标
情境导入
例题讲解
归纳总结
当堂检测
课后作业
1.多边形的外角及外角和的定义;
2.多边形的外角和等于360°;
3.在探求过程中我们使用了观察、归纳的数学方法,并且运用了建模、转化等数学思想.
大家一起来
课堂小结
归纳总结
巩固提升
学习目标
情境导入
例题讲解
当堂检测
课后作业
1.一个多边形的每个内角均为108°,则这个多边形是( )
A.七边形 B.六边形 C.五边形 D.四边形
2.一个多边形的内角和与外角和之比是11∶2,那么这个多边形的边数是( )
A.13 B.12 C.11 D.10
3.正十二边形的每个内角都是 度.
4.一个多边形的内角和是外角和的4倍,则这个多边形是 边形.?
5.一个正多边形,它的一个外角等于与它相邻的内角的 ,
则这个多边形是正 边形.
C
A
十
八
150
归纳总结
巩固提升
学习目标
情境导入
例题讲解
当堂检测
课后作业
6.将两张三角形纸片如图6-4-17摆放,量得
∠1+∠2+∠3+∠4=220°,则∠5= .?
挑战自我
解: ∠1+∠2+∠6=180°,
∠3+∠4+∠7=180°,
∵∠1+∠2+∠3+∠4=220°,
∴∠1+∠2+∠6+∠3+∠4+∠7=360°,
∴∠6+∠7=140°,
∴∠5=180°﹣(∠6+∠7)=40°.
40°
当堂检测
请同学们完成
课本157页习题6.8 T1-T5。
归纳总结
巩固提升
学习目标
情境导入
例题讲解
课后作业
学习改变不了你生命的起点,
但一定能改变你生命的终点。
前路浩浩荡荡,万物皆可期。
同学们,加油!
谢谢
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
