北师大版八年级下册数学课件:1.1 等腰三角形(二)(25张ppt)
文档属性
| 名称 | 北师大版八年级下册数学课件:1.1 等腰三角形(二)(25张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 13.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-07 06:57:59 | ||
图片预览





文档简介
(共25张PPT)
初中数学八年级(下)
第一节 等腰三角形(二)
第一章 三角形的证明
小故事 大智慧
推理证明很重要吆!
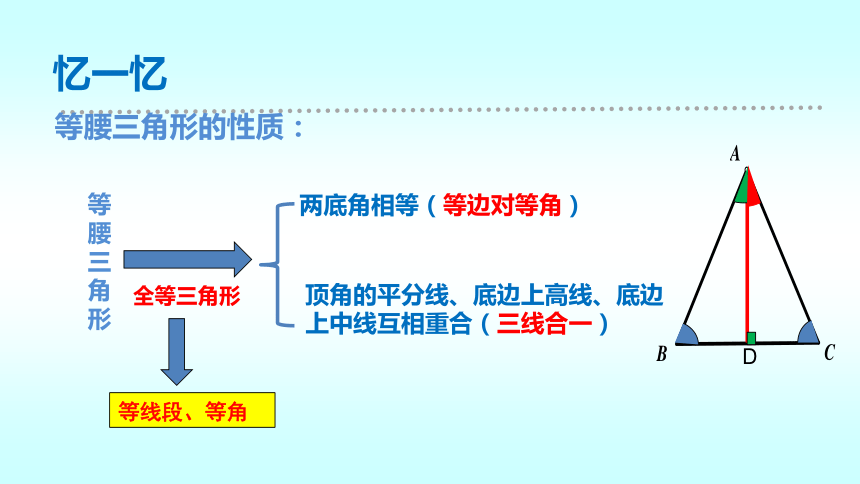
忆一忆
等腰三角形的性质:
等腰三角形
两底角相等(等边对等角)
顶角的平分线、底边上高线、底边上中线互相重合(三线合一)
全等三角形
D
等线段、等角
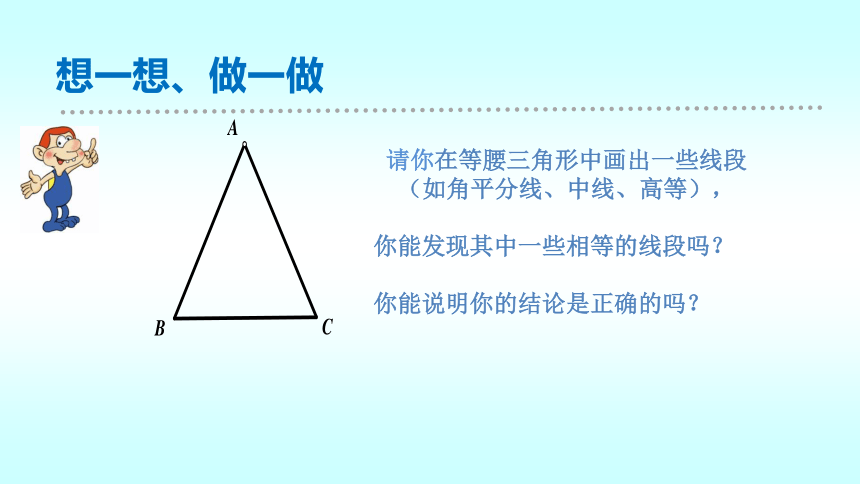
请你在等腰三角形中画出一些线段
(如角平分线、中线、高等),
你能发现其中一些相等的线段吗?
你能说明你的结论是正确的吗?
想一想、做一做
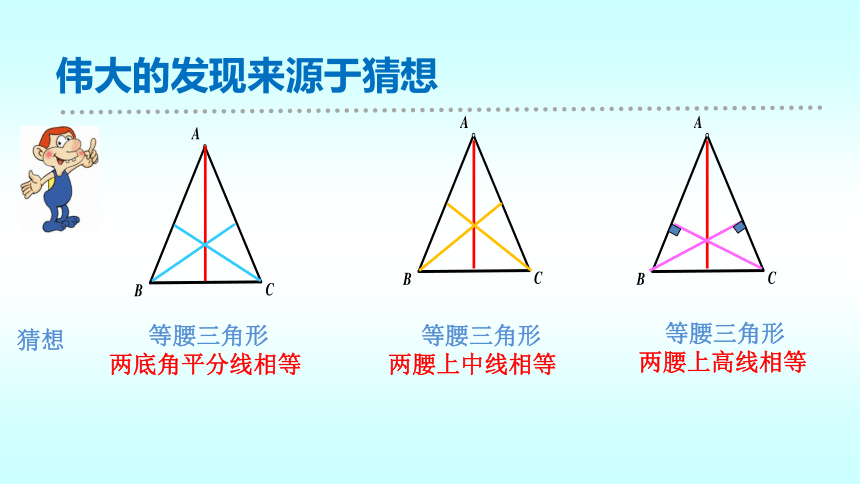
伟大的发现来源于猜想
猜想
等腰三角形
两底角平分线相等
等腰三角形
两腰上中线相等
等腰三角形
两腰上高线相等
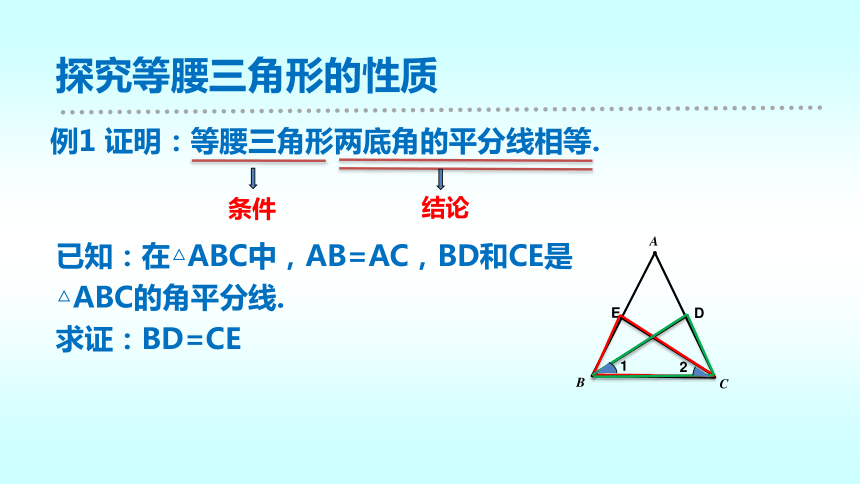
例1 证明:等腰三角形两底角的平分线相等.
探究等腰三角形的性质
条件
结论
D
E
已知:在△ABC中,AB=AC,BD和CE是
△ABC的角平分线.
求证:BD=CE
1
2
探究等腰三角形的性质
D
E
已知:在△ABC中,AB=AC,BD和CE是△ABC的角平分线.
求证:BD=CE
证明∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∵BD、CE分别平分∠ABC和∠ACB,
∴∠1= ∠ABC ∠2= ∠ACB
在△BDC和△CEB中
∵∠ACB=∠ABC BC=CB ∠1=∠2
1
2
∴∠1=∠2
∴△BDC≌△CEB(ASA)
∴BD=CE(全等三角形的对应边相等)
探究等腰三角形的性质
D
E
证法2:∵AB=AC∴∠ABC=∠ACB
∵BD、CE分别平分∠ABC和∠ACB
∴∠3= ∠ABC ∠4= ∠ACB
∴∠3=∠4
在△ABD和△ACE中,
∵∠3=∠4 AB=AC ∠A=∠A
∴△ABD≌△ACE(ASA)
∴BD=CE(全等三角形的对应边相等)
一题多解
3
4
例1 证明:等腰三角形两底角的平分线相等.
反思提升:
条件
结论
D
E
已知:在△ABC中,AB=AC,BD和CE是△ABC的角平分线.
求证:BD=CE
文字语言
证明几何命题的基本步骤
符号语言
图形语言
△BDC≌△CEB
由因导果
执果索因
画
找
写
证
思维拓展:
(1)如果∠ABD= ∠ABC,∠ACE= ∠ACB
那么BD=CE吗?
在△ABC中,AB=AC,点D、E分别在边AC和AB上.
证明∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∵BD、CE分别平分∠ABC和∠ACB
∴∠3= ∠ABC ∠4= ∠ACB
∴∠3=∠4
在△ABD和△ACE中
∵∠3=∠4 AB=AC ∠A=∠A
∴△ABD≌△ACE(ASA)
∴BD=CE(全等三角形的对应边相等)
3
4
思维拓展:
(2)如果∠ABD= ∠ABC,∠ACE= ∠ACB呢?
那么BD=CE吗?
在△ABC中,AB=AC,点D、E分别在边AC和AB上.
(3)如果∠ABD= ∠ABC,∠ACE= ∠ACB呢?
那么BD=CE吗?
由此,你得到什么结论?
等腰三角形两底角的对应n等分线相等
上述的研究过程你得到什么启发?
“特殊” “一般”
重要数学思想方法
类比探究
例2 证明:等腰三角形两腰上的中线相等.
证明:在△ABC中,AB=AC
∵BD、CE是△ABC的中线
∴AD= AC AE= AB
∴AD=AE
在△ADB和△AEC中,
∵AB=AC
∠A=∠A
AD=AE
∴△ADB≌△AEC(SAS)
∴BD=CE(全等三角形的对应边相等)
已知:在△ABC中,AB=AC
BD、CE是△ABC的中线
求证:BD=CE
思维拓展:
在△ABC中,AB=AC,点D、E分别在边AC和AB上.
如果AD= AC,AE= AB,那么BD=CE吗?
如果AD= AC,AE= AB呢?
由此,你能得到什么结论?
等腰三角形两腰上对应n等分线相等
课堂延伸
等腰三角形两腰上的高线相等.
反思提升:
A
B
C
等腰三角形两底角的平分线相等
等腰三角形两腰上的中线相等
等腰三角形两腰上高相等
再探新知:
等边三角形作为特殊的等腰三角形,
它又会有怎样的性质呢?
边:
三边相等
角:
三内角相等,每个内角都等于60°
重要线段:
学以致用:
等边三角形的三个内角都相等,并且每个角都等于60.
已知:如图所示,在△ABC中,AB=AC=BC.
求证:∠A=∠B=∠C=60°
证明:∵AB=AC
∴∠B=∠C(等边对等角)
又∵AC=BC(已知)
∴∠A=∠B(等边对等角)
∴∠A=∠B =∠C
在△ABC中
∵∠A+∠B +∠C=180°
∴ ∠A=∠B=∠C=60°
证明:
定理
再探新知:
等边三角形作为特殊的等腰三角形,
它又会有怎样的性质呢?
边:
三边相等
角:
三内角相等,每个内角都等于60°
重要线段:
(1):每边上“三线合一”
(2):三内角平分线、三边中线、三条高线都相等
学以致用:
求等边三角形两条中线相交所成锐角的度数.
D
E
O
已知: 在△ABC中,AB=AC=BC,△ABC的中线AD、BE相交于点O
求∠BOD的度数.
解: 在△ABC中,
∵AB=AC=BC,AD、BE是△ABC的中线
∴AD⊥BC,BE平分∠ABC
∴∠ADB=90° ∠OBD= ∠ABC=30°(三线合一)
∴∠BOD=903060
反思总结
本节课我们有哪些收获呢?
知识
1等腰三角形中对应线段相等
2 等边三角形性质:边、角、重要线段
等腰三角形
方法
1 命题四步法:找、画、写、证
2 几何证明: 执果索因、由因导果
数学思想
1.转化 “三种”语言转化”
2.“特殊”—“一般”
挑战自我!
2. 如图,已知△ABC是等边三角形,D是AC边上的任意一点,点B,C,E在同一条直线上,且CE=CD,则∠E= 度.
3.证明命题“等腰三角形两腰上的高相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程.下面是小明根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,在△ABC中,AB=AC, .
求证:
请补全已知和求证部分,并写出证明过程.
1.如图,AD,CE分别是△ABC的中线和角平分线,若AB=AC,∠CAD=25°,则∠ACE的度数是( )
A.25° B.50° C.32.5° D.65°
挑战自我!
2. 如图,已知△ABC是等边三角形,D是AC边上的任意一点,点B,C,E在同一条直线上,且CE=CD,则∠E= 度.
1.如图,AD,CE分别是△ABC的中线和角平分线,若AB=AC,∠CAD=25°,则∠ACE的度数是( )
A.25° B.50° C.32.5° D.65°
C
30
3.答案:CE⊥AB,BD⊥AC;CE=BD
证明:∵AB=AC,
∴∠ABC=∠ACB,
∵CE⊥AB,BD⊥AC,
∴∠BEC=∠CDB=90°,
∵BC=BC,
∴△BEC≌△CDB(ASA),
∴CE=BD.
快乐作业!
1.如图,在△ABC中,D、E是BC的三等分点,
且△ADE是等边三角形,则∠BAC= .
4.如图,在一个风筝ABCD中,AB=AD,BC=DC.
(1)分别在AB、AD的中点E,F处拉两根彩线EC,FC,证明这两根彩线的长度相等;
(2)如果AE= AB,AF= AD,那么彩线的长度相等吗?
如果AE= AB,AF= AD呢?由此你能得到什么结论?
(3)除了(1)(2)条件外,你还能在哪些已知条件下得到两根彩线的长度相等的结论?
A组
B组
2.如图,在△ABC中,AB=AC,BD平分∠ABC,交AC于点D,
若BD=BC,则∠A等于多少度?
3.已知:如图,D、E分别是等边三角形ABC的两边AB,
AC上的点,且AD=CE.
求证:CD=BE.
再见
初中数学八年级(下)
第一节 等腰三角形(二)
第一章 三角形的证明
小故事 大智慧
推理证明很重要吆!
忆一忆
等腰三角形的性质:
等腰三角形
两底角相等(等边对等角)
顶角的平分线、底边上高线、底边上中线互相重合(三线合一)
全等三角形
D
等线段、等角
请你在等腰三角形中画出一些线段
(如角平分线、中线、高等),
你能发现其中一些相等的线段吗?
你能说明你的结论是正确的吗?
想一想、做一做
伟大的发现来源于猜想
猜想
等腰三角形
两底角平分线相等
等腰三角形
两腰上中线相等
等腰三角形
两腰上高线相等
例1 证明:等腰三角形两底角的平分线相等.
探究等腰三角形的性质
条件
结论
D
E
已知:在△ABC中,AB=AC,BD和CE是
△ABC的角平分线.
求证:BD=CE
1
2
探究等腰三角形的性质
D
E
已知:在△ABC中,AB=AC,BD和CE是△ABC的角平分线.
求证:BD=CE
证明∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∵BD、CE分别平分∠ABC和∠ACB,
∴∠1= ∠ABC ∠2= ∠ACB
在△BDC和△CEB中
∵∠ACB=∠ABC BC=CB ∠1=∠2
1
2
∴∠1=∠2
∴△BDC≌△CEB(ASA)
∴BD=CE(全等三角形的对应边相等)
探究等腰三角形的性质
D
E
证法2:∵AB=AC∴∠ABC=∠ACB
∵BD、CE分别平分∠ABC和∠ACB
∴∠3= ∠ABC ∠4= ∠ACB
∴∠3=∠4
在△ABD和△ACE中,
∵∠3=∠4 AB=AC ∠A=∠A
∴△ABD≌△ACE(ASA)
∴BD=CE(全等三角形的对应边相等)
一题多解
3
4
例1 证明:等腰三角形两底角的平分线相等.
反思提升:
条件
结论
D
E
已知:在△ABC中,AB=AC,BD和CE是△ABC的角平分线.
求证:BD=CE
文字语言
证明几何命题的基本步骤
符号语言
图形语言
△BDC≌△CEB
由因导果
执果索因
画
找
写
证
思维拓展:
(1)如果∠ABD= ∠ABC,∠ACE= ∠ACB
那么BD=CE吗?
在△ABC中,AB=AC,点D、E分别在边AC和AB上.
证明∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∵BD、CE分别平分∠ABC和∠ACB
∴∠3= ∠ABC ∠4= ∠ACB
∴∠3=∠4
在△ABD和△ACE中
∵∠3=∠4 AB=AC ∠A=∠A
∴△ABD≌△ACE(ASA)
∴BD=CE(全等三角形的对应边相等)
3
4
思维拓展:
(2)如果∠ABD= ∠ABC,∠ACE= ∠ACB呢?
那么BD=CE吗?
在△ABC中,AB=AC,点D、E分别在边AC和AB上.
(3)如果∠ABD= ∠ABC,∠ACE= ∠ACB呢?
那么BD=CE吗?
由此,你得到什么结论?
等腰三角形两底角的对应n等分线相等
上述的研究过程你得到什么启发?
“特殊” “一般”
重要数学思想方法
类比探究
例2 证明:等腰三角形两腰上的中线相等.
证明:在△ABC中,AB=AC
∵BD、CE是△ABC的中线
∴AD= AC AE= AB
∴AD=AE
在△ADB和△AEC中,
∵AB=AC
∠A=∠A
AD=AE
∴△ADB≌△AEC(SAS)
∴BD=CE(全等三角形的对应边相等)
已知:在△ABC中,AB=AC
BD、CE是△ABC的中线
求证:BD=CE
思维拓展:
在△ABC中,AB=AC,点D、E分别在边AC和AB上.
如果AD= AC,AE= AB,那么BD=CE吗?
如果AD= AC,AE= AB呢?
由此,你能得到什么结论?
等腰三角形两腰上对应n等分线相等
课堂延伸
等腰三角形两腰上的高线相等.
反思提升:
A
B
C
等腰三角形两底角的平分线相等
等腰三角形两腰上的中线相等
等腰三角形两腰上高相等
再探新知:
等边三角形作为特殊的等腰三角形,
它又会有怎样的性质呢?
边:
三边相等
角:
三内角相等,每个内角都等于60°
重要线段:
学以致用:
等边三角形的三个内角都相等,并且每个角都等于60.
已知:如图所示,在△ABC中,AB=AC=BC.
求证:∠A=∠B=∠C=60°
证明:∵AB=AC
∴∠B=∠C(等边对等角)
又∵AC=BC(已知)
∴∠A=∠B(等边对等角)
∴∠A=∠B =∠C
在△ABC中
∵∠A+∠B +∠C=180°
∴ ∠A=∠B=∠C=60°
证明:
定理
再探新知:
等边三角形作为特殊的等腰三角形,
它又会有怎样的性质呢?
边:
三边相等
角:
三内角相等,每个内角都等于60°
重要线段:
(1):每边上“三线合一”
(2):三内角平分线、三边中线、三条高线都相等
学以致用:
求等边三角形两条中线相交所成锐角的度数.
D
E
O
已知: 在△ABC中,AB=AC=BC,△ABC的中线AD、BE相交于点O
求∠BOD的度数.
解: 在△ABC中,
∵AB=AC=BC,AD、BE是△ABC的中线
∴AD⊥BC,BE平分∠ABC
∴∠ADB=90° ∠OBD= ∠ABC=30°(三线合一)
∴∠BOD=903060
反思总结
本节课我们有哪些收获呢?
知识
1等腰三角形中对应线段相等
2 等边三角形性质:边、角、重要线段
等腰三角形
方法
1 命题四步法:找、画、写、证
2 几何证明: 执果索因、由因导果
数学思想
1.转化 “三种”语言转化”
2.“特殊”—“一般”
挑战自我!
2. 如图,已知△ABC是等边三角形,D是AC边上的任意一点,点B,C,E在同一条直线上,且CE=CD,则∠E= 度.
3.证明命题“等腰三角形两腰上的高相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程.下面是小明根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,在△ABC中,AB=AC, .
求证:
请补全已知和求证部分,并写出证明过程.
1.如图,AD,CE分别是△ABC的中线和角平分线,若AB=AC,∠CAD=25°,则∠ACE的度数是( )
A.25° B.50° C.32.5° D.65°
挑战自我!
2. 如图,已知△ABC是等边三角形,D是AC边上的任意一点,点B,C,E在同一条直线上,且CE=CD,则∠E= 度.
1.如图,AD,CE分别是△ABC的中线和角平分线,若AB=AC,∠CAD=25°,则∠ACE的度数是( )
A.25° B.50° C.32.5° D.65°
C
30
3.答案:CE⊥AB,BD⊥AC;CE=BD
证明:∵AB=AC,
∴∠ABC=∠ACB,
∵CE⊥AB,BD⊥AC,
∴∠BEC=∠CDB=90°,
∵BC=BC,
∴△BEC≌△CDB(ASA),
∴CE=BD.
快乐作业!
1.如图,在△ABC中,D、E是BC的三等分点,
且△ADE是等边三角形,则∠BAC= .
4.如图,在一个风筝ABCD中,AB=AD,BC=DC.
(1)分别在AB、AD的中点E,F处拉两根彩线EC,FC,证明这两根彩线的长度相等;
(2)如果AE= AB,AF= AD,那么彩线的长度相等吗?
如果AE= AB,AF= AD呢?由此你能得到什么结论?
(3)除了(1)(2)条件外,你还能在哪些已知条件下得到两根彩线的长度相等的结论?
A组
B组
2.如图,在△ABC中,AB=AC,BD平分∠ABC,交AC于点D,
若BD=BC,则∠A等于多少度?
3.已知:如图,D、E分别是等边三角形ABC的两边AB,
AC上的点,且AD=CE.
求证:CD=BE.
再见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
