北师大版八年级下册数学课件:第六章 平行四边形 复习(28张ppt)
文档属性
| 名称 | 北师大版八年级下册数学课件:第六章 平行四边形 复习(28张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-07 06:56:56 | ||
图片预览

文档简介
(共28张PPT)
初中数学八年级(下)
第六章 平行四边形 复习
目标1
目标2
能够熟练掌握平行四边形的判定和性质定理,并能够应用数学符号语言表述证明过程。
掌握三角形中位线的定义和性质,明确三角形中位线与中线的不同并能运用它进行有关的论证和计算。
学习目标
掌握多边形内角和、外角和定理,进一步理解归纳和转化的数学思想。
目标3
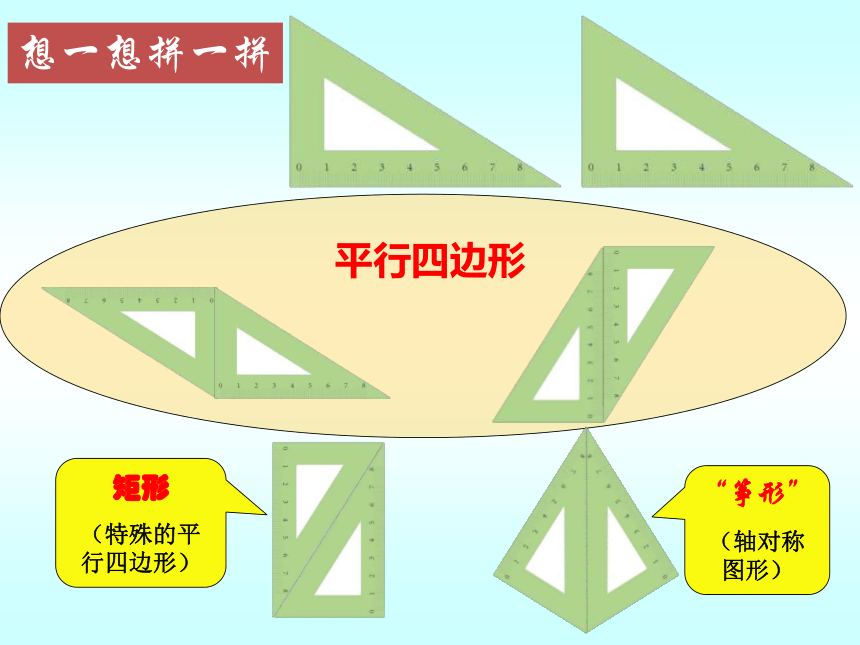
平行四边形
矩形
(特殊的平行四边形)
“筝形”
(轴对称 图形)
想一想拼一拼
几 何 语 言
文字叙述
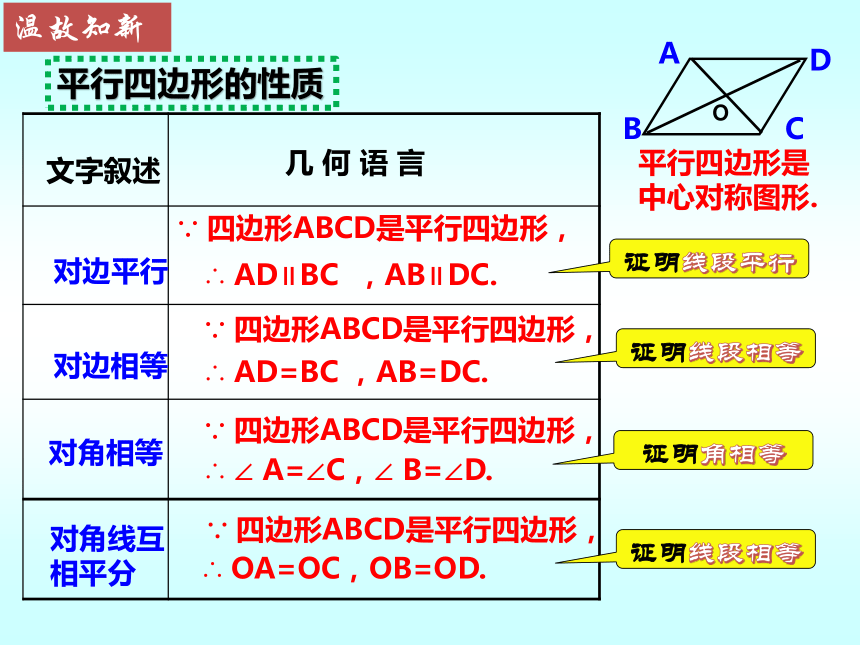
对边平行
对边相等
对角相等
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠ A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
平行四边形的性质
对角线互
相平分
∵ 四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
平行四边形是
中心对称图形.
证明线段相等
证明角相等
证明线段相等
证明线段平行
A
B
C
D
O
温故知新
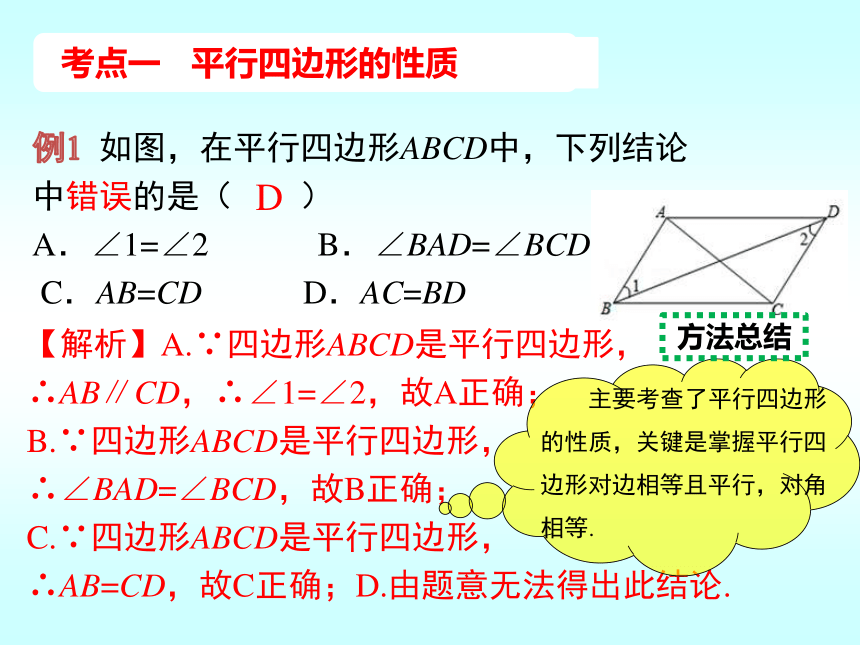
考点一 平行四边形的性质
例1 如图,在平行四边形ABCD中,下列结论中错误的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.AB=CD D.AC=BD
【解析】A.∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠1=∠2,故A正确;
B.∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,故B正确;
C.∵四边形ABCD是平行四边形,
∴AB=CD,故C正确;D.由题意无法得出此结论.
D
主要考查了平行四边形的性质,关键是掌握平行四边形对边相等且平行,对角相等.
方法总结
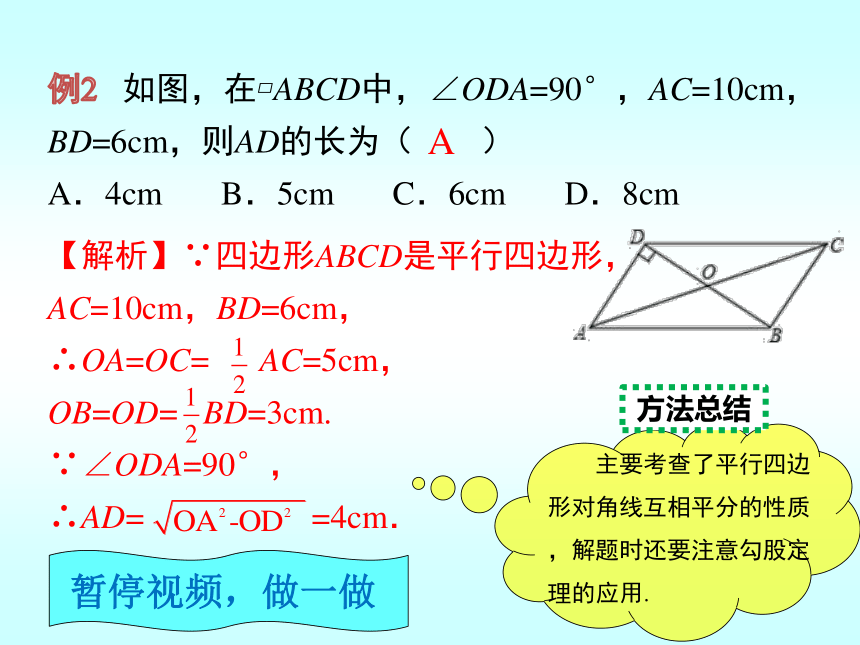
例2 如图,在?ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )
A.4cm B.5cm C.6cm D.8cm
【解析】∵四边形ABCD是平行四边形,
AC=10cm,BD=6cm,
∴OA=OC= AC=5cm,
OB=OD= BD=3cm.
∵∠ODA=90°,
∴AD= =4cm.
A
暂停视频,做一做
主要考查了平行四边形对角线互相平分的性质,解题时还要注意勾股定理的应用.
方法总结
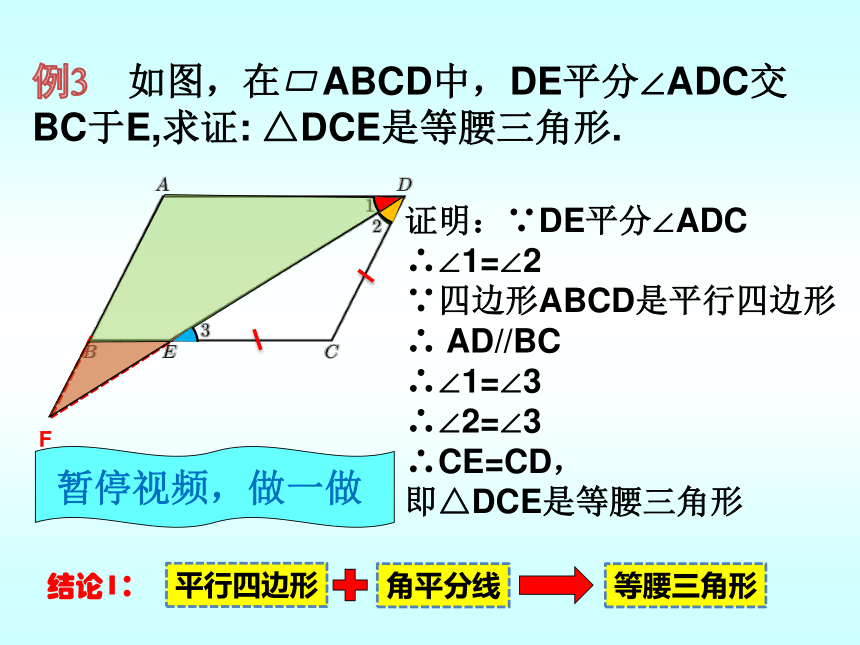
例3 如图,在 ABCD中,DE平分∠ADC交BC于E,求证: △DCE是等腰三角形.
F
证明:∵DE平分∠ADC
∴∠1=∠2
∵四边形ABCD是平行四边形
∴ AD//BC
∴∠1=∠3
∴∠2=∠3
∴CE=CD,
即△DCE是等腰三角形
平行四边形
角平分线
等腰三角形
暂停视频,做一做
结论1:
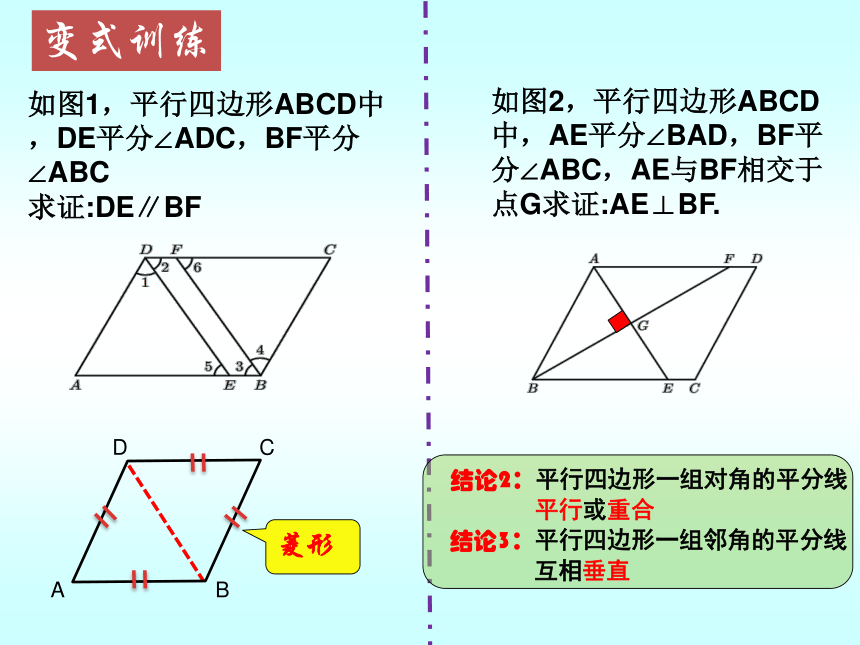
如图1,平行四边形ABCD中,DE平分∠ADC,BF平分∠ABC
求证:DE∥BF
如图2,平行四边形ABCD中,AE平分∠BAD,BF平分∠ABC,AE与BF相交于点G求证:AE⊥BF.
A
B
C
D
变式训练
菱形
结论2:平行四边形一组对角的平分线
平行或重合
结论3:平行四边形一组邻角的平分线
互相垂直
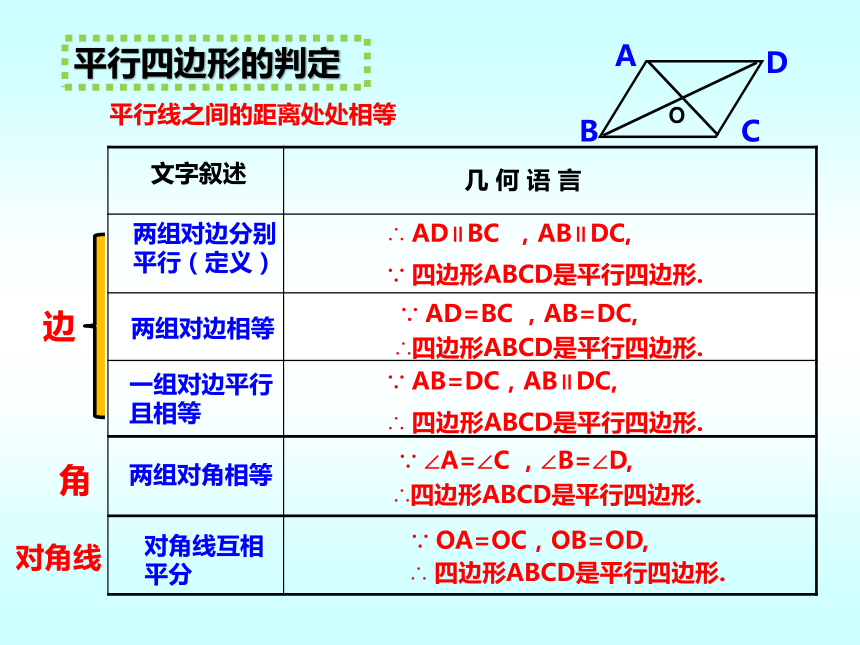
几 何 语 言
文字叙述
两组对边相等
一组对边平行
且相等
∴四边形ABCD是平行四边形.
∵ AD=BC ,AB=DC,
∴ 四边形ABCD是平行四边形.
∵ AB=DC,AB∥DC,
对角线互相
平分
∴ 四边形ABCD是平行四边形.
∵ OA=OC,OB=OD,
两组对边分别
平行(定义)
∵ 四边形ABCD是平行四边形.
∴ AD∥BC ,AB∥DC,
平行线之间的距离处处相等
两组对角相等
∴四边形ABCD是平行四边形.
∵ ∠A=∠C ,∠B=∠D,
边
角
对角线
A
B
C
D
O
平行四边形的判定
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠BAE=∠DFC
又∵AF=CE,∴AE=CF.
在△ABE与△CDF中,
∵
∴△ABE≌△CDF(SAS).
∴BE=DF,∠AEB=∠CFD.
∴180°-∠AEB=180°-∠CFD.
即∠BEF=∠DFE.
∴BE∥DF.
∴四边形BEDF是平行四边形.
(一组对边平行且相等的四边形是平行四边形)
你还能用不同的方法加以证明吗?
例4 如图,E,F是?ABCD的对角线AC上的两点,AF=CE.
求证:四边形BEDF是平行四边形.
考点二 平行四边形的判定
例4 如图,E,F是?ABCD的对角线AC上的两点,AF=CE.
求证:四边形BEDF是平行四边形.
方法2:△ABE≌△CDF
BE∥DF
同理,△ADE≌△CBF
四边形BEDF是平行四边形.
(两组对边分别平行的四边形是平行四边形)
BF∥DE
∠AEB=∠CFD.
∠BEF=∠DFE.
∠DEF=∠BFE.
例4 如图,E,F是?ABCD的对角线AC上的两点,AF=CE.
求证:四边形BEDF是平行四边形.
方法3:△ABE≌△CDF
同理,△ADE≌△CBF
四边形BEDF是平行四边形.
(两组对角分别相等的四边形是平行四边形)
∠AEB=∠CFD.
∠BEF=∠DFE.
∠DEF=∠BFE.
∠EBF=∠FDE.
例4 如图,E,F是?ABCD的对角线AC上的两点,AF=CE.
求证:四边形BEDF是平行四边形.
方法4:△ABE≌△CDF
BE=DF
同理,△ADE≌△CBF
四边形BEDF是平行四边形.
(两组对边分别相等的四边形是平行四边形)
BF=DE
O
例4 如图,E,F是?ABCD的对角线AC上的两点,AF=CE.
求证:四边形BEDF是平行四边形.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
方法5:连接BD,交AC于点O.
平行四边形的性质定理又提供了证明线段平行和相等以及角相等的新方法。
方法总结
又∵AF=CE,
∴AF-OA=CE-OC
即OE=OF.
∴四边形BEDF是平行四边形
(对角线互相平分的四边形是平行四边形)
比较以上方法,你有什么感受?
例5 如图,E、F分别为平行四边形ABCD中AD、BC的中点,分别连接AF、BE交于G,连接CE、DF交于点H,连接EF、GH.证明:EF与GH互相平分.
考点三 平行四边形性质和判定的综合应用
证明:在□ABCD中
∵AD//BC, AD= BC
又 ∵E、F分别为AD、BC中点
∴AE//CF, AE=CF,
DE //BF, DE=BF
∴四边形AECF为平行四边形
四边形DEBF为平行四边形
∴AF//CE, BE //DF
∴四边形EGFH是平行四边形
∴EF与GH互相平分
图形中出现多个平行四边形时要灵活应用平行四边形的性质,找到最简洁的判定方法。
方法总结
暂停视频,做一做
1.三角形的中位线定义:连接三角形两边中点的线段叫做三角形的中位线.
2.三角形的中位线性质:三角形的中位线平行于第三边,并且等于第三边的一半.
三角形的中位线
用符号语言表示
∵DE是△ABC的中位线,
∴DE∥BC, .
例6 如图,四边形ABCD中,AB=CD,G,H分别是BC,AD的中点,BA,CD的延长线分别交GH的延长线于点E,F.求证:∠AEH=∠F.
考点四 三角形的中位线
中点连线——构造中位线——利用中位线性质
方法总结
证明:如图,连接AC,取AC的中点M,
连接HM,GM.
∵H是AD的中点,M是AC的中点,
∴HM是△ADC的中位线
∴HM∥CD,HM= CD.
∴∠1=∠F.
同理,GM∥AB,GM= AB.
∴∠2=∠AEH.
又∵AB=CD,∴GM=HM.
∴∠1=∠2.
∴∠AEH=∠F.
M
1
2
暂停视频,做一做
转化
多边形的内角和与外角和
多边形的内角和等于(n-2) ×180 °
多边形的外角和等于 360 °
正多边形每个内角的度数是
正多边形每个外角的度数是
转化
例7 (2019济南)如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )
A.10 B.11
C.12 D.13
C
设边数为n,根据多边形内角和公式,得
(n-2)×180°=5×360°
解得,n=12
考点五 多边形的内角和与外角和
暂停视频,做一做
例8 如图,小明从点O出发,前进5m后向右转15?,再前进5m后又向右转15?,…这样一直下去,直到他第一次回到出发点O为止,他所走的路径构成了一个多边形。
(1)小明一共走了多少米?
(2)这个多边形的内角和是多少度?
解:(1)∵设这个正多边形边数为n,根据题意得,
∴15n=360,解得n=24,24×5=120m
答:小明一共走了120米;
(2)根据多边形内角和公式,得
(24?2)×180?=3960?,
答:这个多边形的内角和是3960度。
在多边形的有关求边数或内角、外角度数的问题中,要注意内角与外角之间的转化。尤其在求边数的问题中,常常利用定理列出方程,进而再求得边数。
方法总结
本章知识结构
平行四边形
平行四边形
两条平行线距离
三角形中位线
多边形的内角和与外角和
性质
判定
定义
定理
“探索———发现———猜想———证明———应用”
认识图形整体特征
图形各元素(边与角)之间的关系
验证猜想有一般性
3、如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD B.∠BAD=∠BCD,AB∥CD
C.AD∥BC,AD=BC D.AB=CD,AO=CO
2、如图,在?ABCD中,对角线AC和BD交于点O,
AC+BD=38cm,AD= 12cm,则△BOC的周长是( )
A.25cm B.31cm C.37cm D.50cm
B
当堂检测
D
1.平行四边形具有而一般四边形不具有的特征是( )
A、不稳定性 B、对角线互相平分
C、内角的为360度 D、外角和为360度
B
4.若平行四边形的一边长为5,则它的两条对角线长可以是( )
A.12和2 B.3和4 C.4和6 D.4和8
D
5、如图3,平行四边形ABCD中,CD= 10,BC= 12,AE、DF分别平分∠BAD、∠ADC,交BC于E、F,则EF=________.
8
6、一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( ) A. 45° B. 72° C. 60° D. 90°
B
7、已知:如图,在?ABCD中,点E在BC的延长线上,且DE∥AC.请写出BE与BC的数量关系,并证明你的结论.
解:结论:BE=2BC. 证明:∵四边形ABCD为平行四边形, ∴AD=BC,AD∥BC,即AD∥CE. ∵DE∥AC,
∴四边形ADEC为平行四边形. ∴AD=CE.
∴CE=BC.
∴BE=2BC.
作业布置
1、如图,在△ABC中,∠C=90°,CA=CB,
E,F分别为CA,CB上一点,CE=CF,
M,N分别为AF,BE的中点.
求证:AE= MN.
课外拓展
2、如图,在四边形ABCD中,AD∥BC,AD=5,BC=8,M是CD的中点,P是BC边上的一个动点
(点P与点B,C不重合),连接PM并延长交AD的延长线于点Q.
问:当BP取何值时,四边形ABPQ是平行四边形?请说明理由.
课外拓展
寄语
同学们:
只有不断的思考,
才会有新的发现;
只有量的变化,
才会有质的进步.
祝大家学有所得!
初中数学八年级(下)
第六章 平行四边形 复习
目标1
目标2
能够熟练掌握平行四边形的判定和性质定理,并能够应用数学符号语言表述证明过程。
掌握三角形中位线的定义和性质,明确三角形中位线与中线的不同并能运用它进行有关的论证和计算。
学习目标
掌握多边形内角和、外角和定理,进一步理解归纳和转化的数学思想。
目标3
平行四边形
矩形
(特殊的平行四边形)
“筝形”
(轴对称 图形)
想一想拼一拼
几 何 语 言
文字叙述
对边平行
对边相等
对角相等
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠ A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
平行四边形的性质
对角线互
相平分
∵ 四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
平行四边形是
中心对称图形.
证明线段相等
证明角相等
证明线段相等
证明线段平行
A
B
C
D
O
温故知新
考点一 平行四边形的性质
例1 如图,在平行四边形ABCD中,下列结论中错误的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.AB=CD D.AC=BD
【解析】A.∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠1=∠2,故A正确;
B.∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,故B正确;
C.∵四边形ABCD是平行四边形,
∴AB=CD,故C正确;D.由题意无法得出此结论.
D
主要考查了平行四边形的性质,关键是掌握平行四边形对边相等且平行,对角相等.
方法总结
例2 如图,在?ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )
A.4cm B.5cm C.6cm D.8cm
【解析】∵四边形ABCD是平行四边形,
AC=10cm,BD=6cm,
∴OA=OC= AC=5cm,
OB=OD= BD=3cm.
∵∠ODA=90°,
∴AD= =4cm.
A
暂停视频,做一做
主要考查了平行四边形对角线互相平分的性质,解题时还要注意勾股定理的应用.
方法总结
例3 如图,在 ABCD中,DE平分∠ADC交BC于E,求证: △DCE是等腰三角形.
F
证明:∵DE平分∠ADC
∴∠1=∠2
∵四边形ABCD是平行四边形
∴ AD//BC
∴∠1=∠3
∴∠2=∠3
∴CE=CD,
即△DCE是等腰三角形
平行四边形
角平分线
等腰三角形
暂停视频,做一做
结论1:
如图1,平行四边形ABCD中,DE平分∠ADC,BF平分∠ABC
求证:DE∥BF
如图2,平行四边形ABCD中,AE平分∠BAD,BF平分∠ABC,AE与BF相交于点G求证:AE⊥BF.
A
B
C
D
变式训练
菱形
结论2:平行四边形一组对角的平分线
平行或重合
结论3:平行四边形一组邻角的平分线
互相垂直
几 何 语 言
文字叙述
两组对边相等
一组对边平行
且相等
∴四边形ABCD是平行四边形.
∵ AD=BC ,AB=DC,
∴ 四边形ABCD是平行四边形.
∵ AB=DC,AB∥DC,
对角线互相
平分
∴ 四边形ABCD是平行四边形.
∵ OA=OC,OB=OD,
两组对边分别
平行(定义)
∵ 四边形ABCD是平行四边形.
∴ AD∥BC ,AB∥DC,
平行线之间的距离处处相等
两组对角相等
∴四边形ABCD是平行四边形.
∵ ∠A=∠C ,∠B=∠D,
边
角
对角线
A
B
C
D
O
平行四边形的判定
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠BAE=∠DFC
又∵AF=CE,∴AE=CF.
在△ABE与△CDF中,
∵
∴△ABE≌△CDF(SAS).
∴BE=DF,∠AEB=∠CFD.
∴180°-∠AEB=180°-∠CFD.
即∠BEF=∠DFE.
∴BE∥DF.
∴四边形BEDF是平行四边形.
(一组对边平行且相等的四边形是平行四边形)
你还能用不同的方法加以证明吗?
例4 如图,E,F是?ABCD的对角线AC上的两点,AF=CE.
求证:四边形BEDF是平行四边形.
考点二 平行四边形的判定
例4 如图,E,F是?ABCD的对角线AC上的两点,AF=CE.
求证:四边形BEDF是平行四边形.
方法2:△ABE≌△CDF
BE∥DF
同理,△ADE≌△CBF
四边形BEDF是平行四边形.
(两组对边分别平行的四边形是平行四边形)
BF∥DE
∠AEB=∠CFD.
∠BEF=∠DFE.
∠DEF=∠BFE.
例4 如图,E,F是?ABCD的对角线AC上的两点,AF=CE.
求证:四边形BEDF是平行四边形.
方法3:△ABE≌△CDF
同理,△ADE≌△CBF
四边形BEDF是平行四边形.
(两组对角分别相等的四边形是平行四边形)
∠AEB=∠CFD.
∠BEF=∠DFE.
∠DEF=∠BFE.
∠EBF=∠FDE.
例4 如图,E,F是?ABCD的对角线AC上的两点,AF=CE.
求证:四边形BEDF是平行四边形.
方法4:△ABE≌△CDF
BE=DF
同理,△ADE≌△CBF
四边形BEDF是平行四边形.
(两组对边分别相等的四边形是平行四边形)
BF=DE
O
例4 如图,E,F是?ABCD的对角线AC上的两点,AF=CE.
求证:四边形BEDF是平行四边形.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
方法5:连接BD,交AC于点O.
平行四边形的性质定理又提供了证明线段平行和相等以及角相等的新方法。
方法总结
又∵AF=CE,
∴AF-OA=CE-OC
即OE=OF.
∴四边形BEDF是平行四边形
(对角线互相平分的四边形是平行四边形)
比较以上方法,你有什么感受?
例5 如图,E、F分别为平行四边形ABCD中AD、BC的中点,分别连接AF、BE交于G,连接CE、DF交于点H,连接EF、GH.证明:EF与GH互相平分.
考点三 平行四边形性质和判定的综合应用
证明:在□ABCD中
∵AD//BC, AD= BC
又 ∵E、F分别为AD、BC中点
∴AE//CF, AE=CF,
DE //BF, DE=BF
∴四边形AECF为平行四边形
四边形DEBF为平行四边形
∴AF//CE, BE //DF
∴四边形EGFH是平行四边形
∴EF与GH互相平分
图形中出现多个平行四边形时要灵活应用平行四边形的性质,找到最简洁的判定方法。
方法总结
暂停视频,做一做
1.三角形的中位线定义:连接三角形两边中点的线段叫做三角形的中位线.
2.三角形的中位线性质:三角形的中位线平行于第三边,并且等于第三边的一半.
三角形的中位线
用符号语言表示
∵DE是△ABC的中位线,
∴DE∥BC, .
例6 如图,四边形ABCD中,AB=CD,G,H分别是BC,AD的中点,BA,CD的延长线分别交GH的延长线于点E,F.求证:∠AEH=∠F.
考点四 三角形的中位线
中点连线——构造中位线——利用中位线性质
方法总结
证明:如图,连接AC,取AC的中点M,
连接HM,GM.
∵H是AD的中点,M是AC的中点,
∴HM是△ADC的中位线
∴HM∥CD,HM= CD.
∴∠1=∠F.
同理,GM∥AB,GM= AB.
∴∠2=∠AEH.
又∵AB=CD,∴GM=HM.
∴∠1=∠2.
∴∠AEH=∠F.
M
1
2
暂停视频,做一做
转化
多边形的内角和与外角和
多边形的内角和等于(n-2) ×180 °
多边形的外角和等于 360 °
正多边形每个内角的度数是
正多边形每个外角的度数是
转化
例7 (2019济南)如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )
A.10 B.11
C.12 D.13
C
设边数为n,根据多边形内角和公式,得
(n-2)×180°=5×360°
解得,n=12
考点五 多边形的内角和与外角和
暂停视频,做一做
例8 如图,小明从点O出发,前进5m后向右转15?,再前进5m后又向右转15?,…这样一直下去,直到他第一次回到出发点O为止,他所走的路径构成了一个多边形。
(1)小明一共走了多少米?
(2)这个多边形的内角和是多少度?
解:(1)∵设这个正多边形边数为n,根据题意得,
∴15n=360,解得n=24,24×5=120m
答:小明一共走了120米;
(2)根据多边形内角和公式,得
(24?2)×180?=3960?,
答:这个多边形的内角和是3960度。
在多边形的有关求边数或内角、外角度数的问题中,要注意内角与外角之间的转化。尤其在求边数的问题中,常常利用定理列出方程,进而再求得边数。
方法总结
本章知识结构
平行四边形
平行四边形
两条平行线距离
三角形中位线
多边形的内角和与外角和
性质
判定
定义
定理
“探索———发现———猜想———证明———应用”
认识图形整体特征
图形各元素(边与角)之间的关系
验证猜想有一般性
3、如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD B.∠BAD=∠BCD,AB∥CD
C.AD∥BC,AD=BC D.AB=CD,AO=CO
2、如图,在?ABCD中,对角线AC和BD交于点O,
AC+BD=38cm,AD= 12cm,则△BOC的周长是( )
A.25cm B.31cm C.37cm D.50cm
B
当堂检测
D
1.平行四边形具有而一般四边形不具有的特征是( )
A、不稳定性 B、对角线互相平分
C、内角的为360度 D、外角和为360度
B
4.若平行四边形的一边长为5,则它的两条对角线长可以是( )
A.12和2 B.3和4 C.4和6 D.4和8
D
5、如图3,平行四边形ABCD中,CD= 10,BC= 12,AE、DF分别平分∠BAD、∠ADC,交BC于E、F,则EF=________.
8
6、一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( ) A. 45° B. 72° C. 60° D. 90°
B
7、已知:如图,在?ABCD中,点E在BC的延长线上,且DE∥AC.请写出BE与BC的数量关系,并证明你的结论.
解:结论:BE=2BC. 证明:∵四边形ABCD为平行四边形, ∴AD=BC,AD∥BC,即AD∥CE. ∵DE∥AC,
∴四边形ADEC为平行四边形. ∴AD=CE.
∴CE=BC.
∴BE=2BC.
作业布置
1、如图,在△ABC中,∠C=90°,CA=CB,
E,F分别为CA,CB上一点,CE=CF,
M,N分别为AF,BE的中点.
求证:AE= MN.
课外拓展
2、如图,在四边形ABCD中,AD∥BC,AD=5,BC=8,M是CD的中点,P是BC边上的一个动点
(点P与点B,C不重合),连接PM并延长交AD的延长线于点Q.
问:当BP取何值时,四边形ABPQ是平行四边形?请说明理由.
课外拓展
寄语
同学们:
只有不断的思考,
才会有新的发现;
只有量的变化,
才会有质的进步.
祝大家学有所得!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
