人教A版高中数学选修4-5不等式题型全归纳 学案(含答案)
文档属性
| 名称 | 人教A版高中数学选修4-5不等式题型全归纳 学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-08 00:00:00 | ||
图片预览




文档简介
一、均值不等式在证明中的应用
1. (1)已知,求证:;
(2)已知实数 满足:,试利用(1)求的最小值。
(1)证:
(当且仅当时,取等号);
(2)解:,当且仅当时,的最小值是。
考点:均值不等式在证明中的应用、综合法证明不等式
二、绝对值不等式
2. 已知函数若函数恰有个零点,则实数的取值范围为_______.
答案:
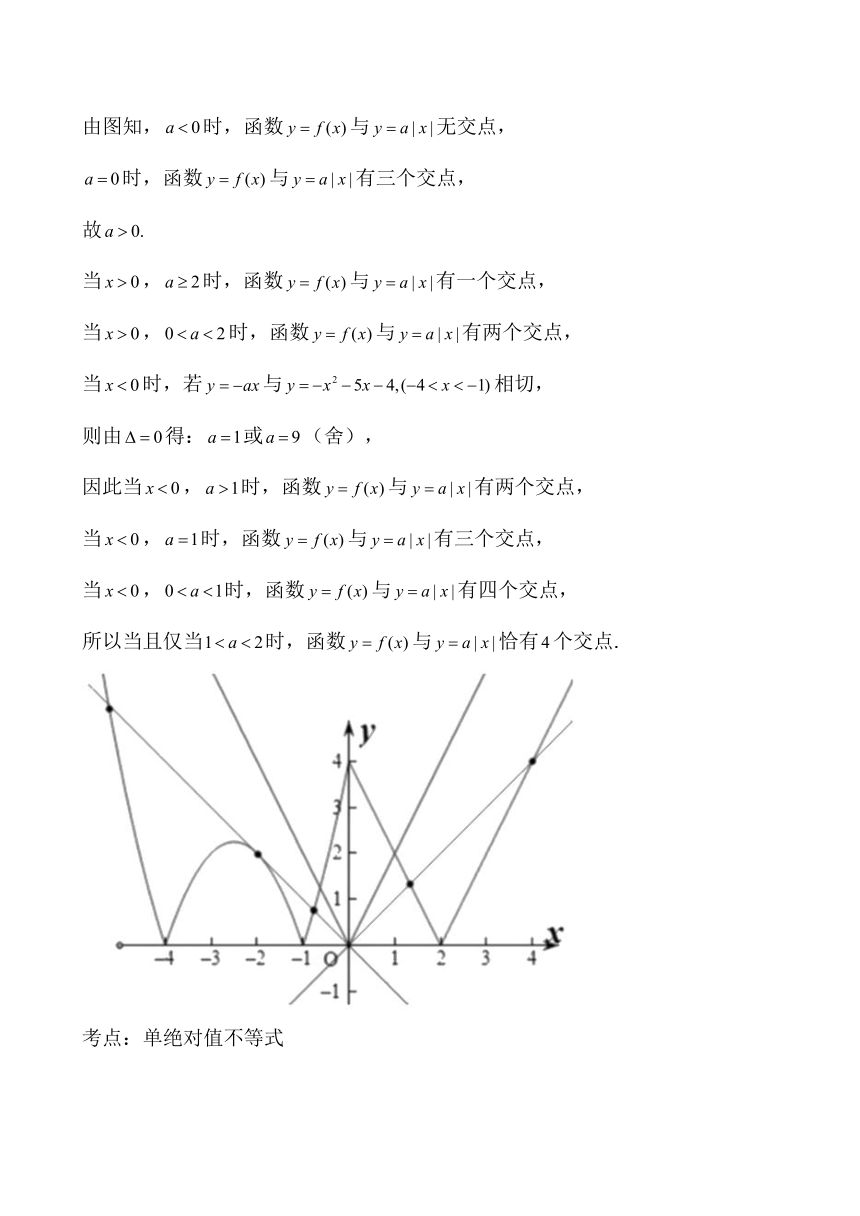
解析:分别作出函数与的图像,
由图知,时,函数与无交点,
时,函数与有三个交点,
故
当,时,函数与有一个交点,
当,时,函数与有两个交点,
当时,若与相切,
则由得:或(舍),
因此当,时,函数与有两个交点,
当,时,函数与有三个交点,
当,时,函数与有四个交点,
所以当且仅当时,函数与恰有个交点.
考点:单绝对值不等式
3. 存在 ,使得不等式 成立,则实数 的取值范围为_____________
答案:?
解析:不等式 ,即 ,
令 的图象是关于 对称的一个 字形图形,其象位于第一、二象限;
,是一个开口向下,关于 轴对称,最大值为 的抛物线;
要存在 ,使不等式 成立,
则 的图象应该在第二象限和 的图象有交点,
两种临界情况,①当 时,的右半部分和 在第二象限相切:
的右半部分即 ,
联列方程 ,只有一个解;
即 ,即 ,?,得: ;
此时 恒大于等于 ,所以取不到;
所以 ;
②当 时,要使 和 在第二象限有交点,
即 的左半部分和 的交点的位于第二象限;
无需联列方程,只要 与 轴的交点小于 即可;
与 轴的交点为 ,所以 ,
又因为 ,所以 ;
综上,实数 的取值范围是: ;
故答案为:.
考点:单绝对值不等式
4. 已知函数,.
(1)当时,求不等式的解集;
(2)设,且当时,,求的取值范围。
(1)当时,令,
作出函数图像可知,当时,,
故原不等式的解集为;
(2)依题意,原不等式化为,
故对都成立,
故,
故,
故的取值范围是.
考点:同系数绝对值相加型不等式
5. 已知函数
(1)证明:
(2)求不等式的解集。
(1)
当时,,所以,
(2)由(1)可知
当 时,的解集为空集;
当时,的解集为?
当 时,的解集为
综上:不等式的解集:
考点:同系数绝对值相减型不等式
6. 设函数
(1)求不等式的解集;
(2)若恒成立,求实数的取值范围.
(1)由题意得?
当 时,不等式化为,解得,
当时,不等式化为,解得,
当时,不等式化为,解得,
综上,不等式的解集为.
(2)由(1)得 ,若, 恒成立,
则只需 ,解得 ,
综上,的取值范围为?
考点:不同系数绝对值相加减型不等式
7. 设函数
(1)当时,求不等式的解集;
(2)如果不等式的解集为,求的值。
(1)当时,可化为。
???????? 由此可得? 或。
???????? 故不等式的解集为或。
?(2) 由 得
???????? 此不等式化为不等式组 ?? 或
即 或
???????? 因为,所以不等式组的解集为
???????? 由题设可得,故
考点:已知绝对值不等式解求参数
8. 已知函数.
(1)当时,求不等式的解集;
(2)若的解集包含,求的取值范围.?
答案:
(1)当时,
?所以不等式可化为,或,或
解得或
因此不等式的解集为或
(2)由已知
即为,
也即
若的解集包含 ,
则,,
也就是,,
所以,,
从而,
解得
因此的取值范围为.
考点:已知绝对值不等式解的范围求参数范围、同系数绝对值不等式相加减
9. 已知函数,
(1)若对任意的有成立,求的取值范围;
(2)若不等式,对于任意的都成立,求的取值范围。
(1)根据题意, 小于等于 的最小值
由?
可得
所以
(2)当 即 时, 恒成立,
当 时,由绝对值不等式得性质可得
,
当且仅当 时取 , 恒成立,
,
,
?
考点:含绝对值不等式的恒成立问题、同系数绝对值相加型不等式
10. 已知函数 .
(1)求 的取值范围,使 为常数函数.
(2)若关于 的不等式 有解,求实数 的取值范围.
(1)
则当 时, 为常数函数.
(2)方法一:如图,结合(1)知函数的最小值为 ,
实数 的取值范围为 .
方法二: ;
,
等号当且仅当 时成立.
得函数 的最小值为 ,则实数 的取值范围为 .
考点:含绝对值不等式的能成立问题
11. 已知实数满足:求证:.
证明:,
由题设
.
.
考点:绝对值的三角不等式
12. 已知函数.
(1)求的解集;
(2)设函数,,若对任意的都成立,求实数的取值范围.
(1),
,即,
① 或② 或③
解得不等式①:;②:无解;③:,
所以的解集为或.???????????????????
(2)即的图象恒在图象的上方,
可以作出的图象,
而图象为恒过定点,且斜率变化的一条直线,
作出函数图象, ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
其中 ,,
由图可知,要使得的图象恒在图象的上方,
实数的取值范围应该为. ?
?? ?
考点:同系数绝对值不等式相加型、 ?数形结合在含参绝对值不等式中的应用? ? ?
三、证明不等式的基本方法
13. 设不等式的解集是,.
(1)试比较与的大小;
(2)设表示数集的最大数.求证:
答案:(1)(2)见解析
解析:(1)先解出
.
问题得证.
(2)
可知,
所以根据不等式的性质,同向正向不等式具有可乘性,从而可证出.
故.
考点:比较法证明不等式
14. 已知,不等式的解集为.
(1)求;
(2)当时,证明:.
(1)解不等式: ;
? 或? 或
或或,
. ? ? ? ? ? ? ? ? ? ? ??
(2)需证明:,
只需证明,
即需证明
,
所以原不等式成立.?
考点:分析法证明不等式
15. 设 且证明:
(1) ;
(2) 与 不可能同时成立.
由, 得
(1)由基本不等式及 ,有 ,即;
(2)假设与同时成立,
则由 及 得 ,
同理 ,
从而 ,这与 矛盾,
故 与 不可能同时成立.
考点:反证法证明不等式、均值不等式在证明中的应用
16. 已知数列的前项和满足.
(1)求数列的通项公式;
(2)设,记数列的前和为,证明:.
【答案】(1);(2)详见解析.
【解析】
试题分析:(1)考虑到,因此可以利用条件中的式子得到数列的一个递推公式,从而即可求解;(2)由(1)可知,,从而可证,进一步放缩可得,求和即可得证.
试题解析:(1)∵,当时, ,又∵,与两边分别相减得,得,又∵,
∴数列是以为首项,为公比的等比数列,∴,得;
∵,∴,,得,又∵,∴
,∴.
四、柯西不等式
17. 已知关于的不等式的解集为
求实数 的值;
求的最大值.
由,
得
则,
解得
当且仅当即时等号成立,
故.
考点:柯西不等式的代数形式
18. 已知函数且的解集为,
求的值;
若且求证
(1)
的解集是
故.
由知
由柯西不等式得
考点:一般的柯西不等式
