青岛版数学七上1.3 线段、射线和直线(线段初步)课件(49张)
文档属性
| 名称 | 青岛版数学七上1.3 线段、射线和直线(线段初步)课件(49张) |  | |
| 格式 | zip | ||
| 文件大小 | 22.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-08 18:50:18 | ||
图片预览











文档简介
(共49张PPT)
数学
讲次名称:线段初步
定义、规范及公理
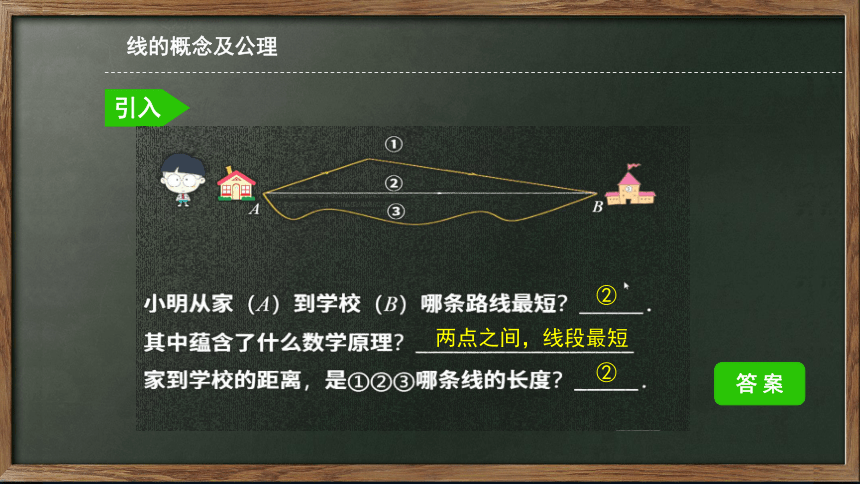
图中的三种线,你还记得多少?
线的概念及公理
引入
线的概念及公理
答 案
笔记
0
1
2
不能
不能
能
线的概念及公理
答 案
笔记
大写
大写
小写
小写
端点字母写在前
大写
小写
我们学习了直线、射线和线段,为什么直线和线段
都可以用两个无顺序的大写字母表示呢?
一根钉子可以固定木条吗?两根钉子呢?
其中蕴含了什么数学原理?
线的概念及公理
引入
思考
钉子
线的概念及公理
笔记
确定 一条直线.
答 案
两点
线的概念及公理
引入
答 案
②
两点之间,线段最短
②
线的概念及公理
答 案
笔记
线段
长度
距离
【示例】
下列说法正确的个数为( )
(1)过两点有且只有一条直线;
(2)连接两点的线段叫做两点间的距离;
(3)两点之间的所有连线中,线段最短;
(4)直线AB和直线BA表示同一条直线.
A.1 B.2 C.3 D.4
线的概念及公理
答 案
D
答 案
总结
例1
答 案
①③⑤
(1).下列说法正确的是 .
①线段AB可表示为线段BA;
②射线AB可表示为射线BA;
③延长线段AB;
④延长直线AB;
⑤线段AB和射线AB都是直线AB的一部分;
⑥直线比射线长,射线比线段长
(2).下列说法正确的是( )
A.射线AB的长度为12cm
B.线段AB叫做A、B两点间的距离
C.直线、线段、射线中直线最长
D.延长线段BA到C,使得AC=BA
例1
答 案
D
例1
答 案
A
(3).在墙壁上用两个钉子就能固定一根横放的木条,这样做根据的道理是( )
A.两点确定一条直线 B.两点确定一条线段
C.两点之间,直线最短 D.两点之间,线段最短
(4).现实生活中“为何有人乱穿马路,却不愿从天桥或斑马线通过?”,请用数学知识解释这一现象,其原因为( )
A.两点之间线段的长度,叫做这两点之间的距离
B.过一点有无数条直线
C.两点确定一条直线
D.两点之间,线段最短
例1
答 案
D
练习1.1
答 案
C
(1).如图所示,A、B、C是同一直线上的三点,下列说法正确的是( )
A.射线AB与射线BA是同一条射线
B.射线AB与射线BC是同一条射线
C.射线AB与射线AC是同一条射线
D.射线BA与射线BC是同一条射线
练习1.1
答 案
A
作图与计算
分析:有 的才可以延长,并注意延长方向,
而直线是无 的,无需延长
根据题意画直线、射线、线段或者延长线段
答 案
端点
引入
端点
思考:线段AB也想像直线那样无限延伸,
怎么作它的延长线呢?
根据题意画直线、射线、线段或者延长线段
答 案
无
讲解
无
我也想无限延伸!!
---------
---------
---------
无
延长线段AB指的是:
从线段AB的端点 到端点 的方向 。
反向延长线:与延长线方向 的延长线.
根据题意画直线、射线、线段或者延长线段
答 案
A
B
笔记
延长
相反
请画出射线BC的反向延长线.
C B
请画出线段AB的延长线.
A B
请画出线段AB的反向延长线.
A B
根据题意画直线、射线、线段或者延长线段
答 案
-------------
单步训练
作延长线和反向延长线注意看清楚字母顺序.
-------------
-------------
笔记
答 案
如图,点C是线段AB外一点,按下列语句画图:
(1)画射线CB;
(2)反向延长线段AB;
(3)连接AC
例2
答 案
解:如图所示:
练习2.1
B
解:如图所示:
解析:(1)利用线段的定义得出答案;
(2)利用直线的定义画出即可;
(3)利用射线的定义得出即可;
(4)利用延长线的定义得出即可.
答 案
思考
如何用圆规比较AB、CD的长短?
作线段等于已知线段或者已知线段和差
作线段等于已知线段或者已知线段和差
答 案
ABAB=CD
讲解
AB>CD
思考
如何用尺规作图作 AC=a+b?
作线段等于已知线段或者已知线段和差
答 案
作线段等于已知线段或者已知线段和差
笔记
用无刻度的直尺和圆规作图,叫做尺规 .
答 案
作图
如何用尺规作图作AC=a-b?
作线段等于已知线段或者已知线段和差
答 案
单步训练
尺规作图中,直尺用来画直线;圆规用来截等长.
总结
答 案
例3
答 案
解:如图所示:
练习3.1
答 案
A
解析
因为AB=m,BC=n,所以AC=AB-BC=m-n,
所以所求线段是AC.故选:A.
如图,线段AB,在平面内找一点C,使得CA=CB.
思考:点C是线段AB的中点吗?
线段中点(n等分点)的概念及计算
答 案
引入
A
B
把一条线段分成相等的两条线段的点,叫做线段的 。
如图,M点把线段平均分成两份,则AM= = AB,
M点叫做线段AB的 .
线段中点(n等分点)的概念及计算
答 案
中点
BM
笔记
中点
线段中点(n等分点)的概念及计算
答 案
5
5
单步训练
10
20
中点
线段中点(n等分点)的概念及计算
答 案
1
2
讲解
3
n-1
线段中点(n等分点)的概念及计算
答 案
4.5cm
3cm或6cm
单步训练
2.25cm或4.5cm或6.75cm
线段中点(n等分点)的概念及计算
答 案
2cm
3cm或6cm
单步训练
出现n等分点,注意多种情况 。
笔记
答 案
12cm或6cm或4cm
【示例】如图,若C是AD的中点,且AD=6,AB=10,
则BC= .
线段中点(n等分点)的概念及计算
答 案
CD
3
思路点拨
AC
3
7
DB
3
4
7
线段计算就是线段之间的加减或比例关系问题.
笔记
答 案
如图所示,点C、D是线段AB上两点,点D是AD的中点,若
BC=6cm,BD=10cm.
(1)求线段CD的长度;
(2)求线段AB的长度.
例4
答 案
如图,C、D是线段AB上的两点,D是AC的中点,若BC=2cm,AD/BD=2/3,求AB的长度。
练习4.1
答 案
已知M是线段AB上的一点,下列各式中不能判定M是线段AB中点的是( )
A. AB=2AM B. BM=AB/2
C. AM=BM D. AM+BM=AB
例5
答 案
D
如果点C在直线AB上,下列表达式:①AC=AB/2;②AB=2BC;③AC=BC;④AC+BC=AB中,能表示C是AB中点的有( )
A.1个 B.2个 C.3个 D.4个
练习5.1
答 案
A
解析
解:①当AC=AB/2时,当点C不在线段AB上时,点C不是AB的中点,故本题错误;②当AB=2BC时,当点C不在线段AB上时,点C不是AB的中点,故本题错误;③当AC=BC时,点C是AB的中点故本小题正确;④当AC+BC=AB时,点C不一定是AB的中点,故本题错误.
故选:A.
【示例1】已知线段AB=10cm,直线AB上有一点C,BC=4cm,则线段AC= cm.
【示例2】已知线段AB=10cm,直线AB上有一点C,BC=4cm,
点D是线段AC的中点,则线段AB= cm.
【示例3】点A、B、C、D在同一条直线上,AB=1cm,BC=4cm,CD=2cm,则线段AD= cm.
线段计算分类讨论
答 案
6或14
7或3
1或3或5或7
有图有真相,无图有坑,注意分类讨论.
总结
答 案
在直线l上顺次取A、B、C三点,且线段AB=5cm,BC=3cm,那么A,C两点间的距离是( )
A.8cm B.2cm C.2cm或8cm D.无法确定
例6
答 案
A
解:因为AB=5cm,BC=3cm,
所以AC=AB+BC=8cm.
故选A.
解析
已知线段AB=10cm,在直线AB上有一点C,且线段BC=4cm,点M是线段AC的中点,则AM= .
练习6.1
答 案
3cm或7cm
解析
解:①当点C在点AB之间时,
因为线段AB=10cm,BC=4cm
所以AC=10-4=6cm.
因为M是线段AC的中点,所以AM=AC/2=3cm.
②当点C在点B的右侧时,
因为线段AB=10cm,BC=4cm,
所以AC=14cm.
因为M是线段AC的中点,所以AM=AC/2=7cm.
综上所述,线段AM的长为3cm或7cm.
已知点C是线段AB的中点,点D在直线AB上,BD=AB/3,若AD=16,则CD= .
例7
答 案
4或10
解析
故答案为4或10.
直线上有A,B,C三点,点M是线段AB的中点,点N是线段BC的一个三等分点,如果AB=6,BC=12,求线段MN的长度。
练习7.1
答 案
直线上有A,B,C三点,点M是线段AB的中点,点N是线段BC的一个三等分点,如果AB=6,BC=12,求线段MN的长度。
练习7.1
答 案
解析
分类讨论:点C在AB延长线上,点C在BA的延长线上,根据线段的中点,三等分点的性质,可得BM、BN的长,根据线段的和差,可得答案.
Thank you
数学
讲次名称:线段初步
定义、规范及公理
图中的三种线,你还记得多少?
线的概念及公理
引入
线的概念及公理
答 案
笔记
0
1
2
不能
不能
能
线的概念及公理
答 案
笔记
大写
大写
小写
小写
端点字母写在前
大写
小写
我们学习了直线、射线和线段,为什么直线和线段
都可以用两个无顺序的大写字母表示呢?
一根钉子可以固定木条吗?两根钉子呢?
其中蕴含了什么数学原理?
线的概念及公理
引入
思考
钉子
线的概念及公理
笔记
确定 一条直线.
答 案
两点
线的概念及公理
引入
答 案
②
两点之间,线段最短
②
线的概念及公理
答 案
笔记
线段
长度
距离
【示例】
下列说法正确的个数为( )
(1)过两点有且只有一条直线;
(2)连接两点的线段叫做两点间的距离;
(3)两点之间的所有连线中,线段最短;
(4)直线AB和直线BA表示同一条直线.
A.1 B.2 C.3 D.4
线的概念及公理
答 案
D
答 案
总结
例1
答 案
①③⑤
(1).下列说法正确的是 .
①线段AB可表示为线段BA;
②射线AB可表示为射线BA;
③延长线段AB;
④延长直线AB;
⑤线段AB和射线AB都是直线AB的一部分;
⑥直线比射线长,射线比线段长
(2).下列说法正确的是( )
A.射线AB的长度为12cm
B.线段AB叫做A、B两点间的距离
C.直线、线段、射线中直线最长
D.延长线段BA到C,使得AC=BA
例1
答 案
D
例1
答 案
A
(3).在墙壁上用两个钉子就能固定一根横放的木条,这样做根据的道理是( )
A.两点确定一条直线 B.两点确定一条线段
C.两点之间,直线最短 D.两点之间,线段最短
(4).现实生活中“为何有人乱穿马路,却不愿从天桥或斑马线通过?”,请用数学知识解释这一现象,其原因为( )
A.两点之间线段的长度,叫做这两点之间的距离
B.过一点有无数条直线
C.两点确定一条直线
D.两点之间,线段最短
例1
答 案
D
练习1.1
答 案
C
(1).如图所示,A、B、C是同一直线上的三点,下列说法正确的是( )
A.射线AB与射线BA是同一条射线
B.射线AB与射线BC是同一条射线
C.射线AB与射线AC是同一条射线
D.射线BA与射线BC是同一条射线
练习1.1
答 案
A
作图与计算
分析:有 的才可以延长,并注意延长方向,
而直线是无 的,无需延长
根据题意画直线、射线、线段或者延长线段
答 案
端点
引入
端点
思考:线段AB也想像直线那样无限延伸,
怎么作它的延长线呢?
根据题意画直线、射线、线段或者延长线段
答 案
无
讲解
无
我也想无限延伸!!
---------
---------
---------
无
延长线段AB指的是:
从线段AB的端点 到端点 的方向 。
反向延长线:与延长线方向 的延长线.
根据题意画直线、射线、线段或者延长线段
答 案
A
B
笔记
延长
相反
请画出射线BC的反向延长线.
C B
请画出线段AB的延长线.
A B
请画出线段AB的反向延长线.
A B
根据题意画直线、射线、线段或者延长线段
答 案
-------------
单步训练
作延长线和反向延长线注意看清楚字母顺序.
-------------
-------------
笔记
答 案
如图,点C是线段AB外一点,按下列语句画图:
(1)画射线CB;
(2)反向延长线段AB;
(3)连接AC
例2
答 案
解:如图所示:
练习2.1
B
解:如图所示:
解析:(1)利用线段的定义得出答案;
(2)利用直线的定义画出即可;
(3)利用射线的定义得出即可;
(4)利用延长线的定义得出即可.
答 案
思考
如何用圆规比较AB、CD的长短?
作线段等于已知线段或者已知线段和差
作线段等于已知线段或者已知线段和差
答 案
AB
讲解
AB>CD
思考
如何用尺规作图作 AC=a+b?
作线段等于已知线段或者已知线段和差
答 案
作线段等于已知线段或者已知线段和差
笔记
用无刻度的直尺和圆规作图,叫做尺规 .
答 案
作图
如何用尺规作图作AC=a-b?
作线段等于已知线段或者已知线段和差
答 案
单步训练
尺规作图中,直尺用来画直线;圆规用来截等长.
总结
答 案
例3
答 案
解:如图所示:
练习3.1
答 案
A
解析
因为AB=m,BC=n,所以AC=AB-BC=m-n,
所以所求线段是AC.故选:A.
如图,线段AB,在平面内找一点C,使得CA=CB.
思考:点C是线段AB的中点吗?
线段中点(n等分点)的概念及计算
答 案
引入
A
B
把一条线段分成相等的两条线段的点,叫做线段的 。
如图,M点把线段平均分成两份,则AM= = AB,
M点叫做线段AB的 .
线段中点(n等分点)的概念及计算
答 案
中点
BM
笔记
中点
线段中点(n等分点)的概念及计算
答 案
5
5
单步训练
10
20
中点
线段中点(n等分点)的概念及计算
答 案
1
2
讲解
3
n-1
线段中点(n等分点)的概念及计算
答 案
4.5cm
3cm或6cm
单步训练
2.25cm或4.5cm或6.75cm
线段中点(n等分点)的概念及计算
答 案
2cm
3cm或6cm
单步训练
出现n等分点,注意多种情况 。
笔记
答 案
12cm或6cm或4cm
【示例】如图,若C是AD的中点,且AD=6,AB=10,
则BC= .
线段中点(n等分点)的概念及计算
答 案
CD
3
思路点拨
AC
3
7
DB
3
4
7
线段计算就是线段之间的加减或比例关系问题.
笔记
答 案
如图所示,点C、D是线段AB上两点,点D是AD的中点,若
BC=6cm,BD=10cm.
(1)求线段CD的长度;
(2)求线段AB的长度.
例4
答 案
如图,C、D是线段AB上的两点,D是AC的中点,若BC=2cm,AD/BD=2/3,求AB的长度。
练习4.1
答 案
已知M是线段AB上的一点,下列各式中不能判定M是线段AB中点的是( )
A. AB=2AM B. BM=AB/2
C. AM=BM D. AM+BM=AB
例5
答 案
D
如果点C在直线AB上,下列表达式:①AC=AB/2;②AB=2BC;③AC=BC;④AC+BC=AB中,能表示C是AB中点的有( )
A.1个 B.2个 C.3个 D.4个
练习5.1
答 案
A
解析
解:①当AC=AB/2时,当点C不在线段AB上时,点C不是AB的中点,故本题错误;②当AB=2BC时,当点C不在线段AB上时,点C不是AB的中点,故本题错误;③当AC=BC时,点C是AB的中点故本小题正确;④当AC+BC=AB时,点C不一定是AB的中点,故本题错误.
故选:A.
【示例1】已知线段AB=10cm,直线AB上有一点C,BC=4cm,则线段AC= cm.
【示例2】已知线段AB=10cm,直线AB上有一点C,BC=4cm,
点D是线段AC的中点,则线段AB= cm.
【示例3】点A、B、C、D在同一条直线上,AB=1cm,BC=4cm,CD=2cm,则线段AD= cm.
线段计算分类讨论
答 案
6或14
7或3
1或3或5或7
有图有真相,无图有坑,注意分类讨论.
总结
答 案
在直线l上顺次取A、B、C三点,且线段AB=5cm,BC=3cm,那么A,C两点间的距离是( )
A.8cm B.2cm C.2cm或8cm D.无法确定
例6
答 案
A
解:因为AB=5cm,BC=3cm,
所以AC=AB+BC=8cm.
故选A.
解析
已知线段AB=10cm,在直线AB上有一点C,且线段BC=4cm,点M是线段AC的中点,则AM= .
练习6.1
答 案
3cm或7cm
解析
解:①当点C在点AB之间时,
因为线段AB=10cm,BC=4cm
所以AC=10-4=6cm.
因为M是线段AC的中点,所以AM=AC/2=3cm.
②当点C在点B的右侧时,
因为线段AB=10cm,BC=4cm,
所以AC=14cm.
因为M是线段AC的中点,所以AM=AC/2=7cm.
综上所述,线段AM的长为3cm或7cm.
已知点C是线段AB的中点,点D在直线AB上,BD=AB/3,若AD=16,则CD= .
例7
答 案
4或10
解析
故答案为4或10.
直线上有A,B,C三点,点M是线段AB的中点,点N是线段BC的一个三等分点,如果AB=6,BC=12,求线段MN的长度。
练习7.1
答 案
直线上有A,B,C三点,点M是线段AB的中点,点N是线段BC的一个三等分点,如果AB=6,BC=12,求线段MN的长度。
练习7.1
答 案
解析
分类讨论:点C在AB延长线上,点C在BA的延长线上,根据线段的中点,三等分点的性质,可得BM、BN的长,根据线段的和差,可得答案.
Thank you
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
