高一物理人教版必修2课件:第五章 曲线运动40张PPT
文档属性
| 名称 | 高一物理人教版必修2课件:第五章 曲线运动40张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-07 15:39:50 | ||
图片预览








文档简介
(共40张PPT)
第五章
曲线运动
专题整合
自我检测
学案9 章末总结
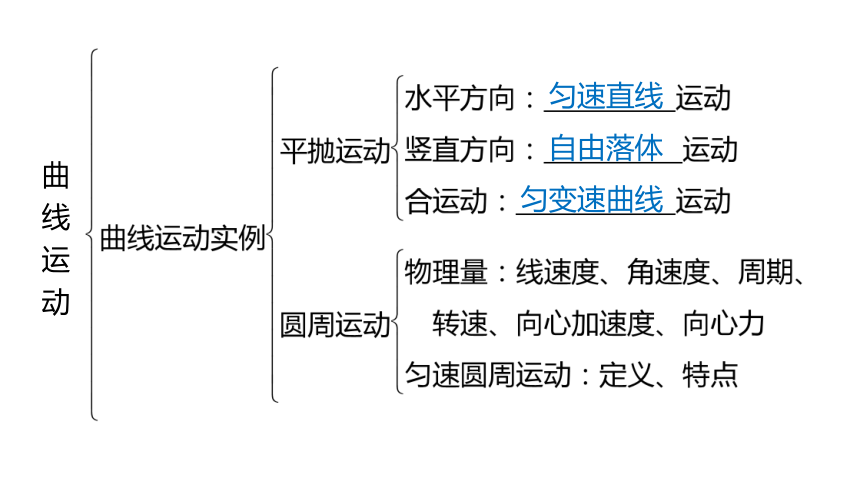
网络构建
网络构建
切线
物体所受合力的方向与
它的速度方向不在同一直线上
平行四边形定则
曲线运动
匀速直线
自由落体
匀变速曲线
曲线运动
曲线运动实例
圆周运动
竖直平面内的圆周运动
最高点速度恰好为零
0
一、运动的合成和分解
专题整合
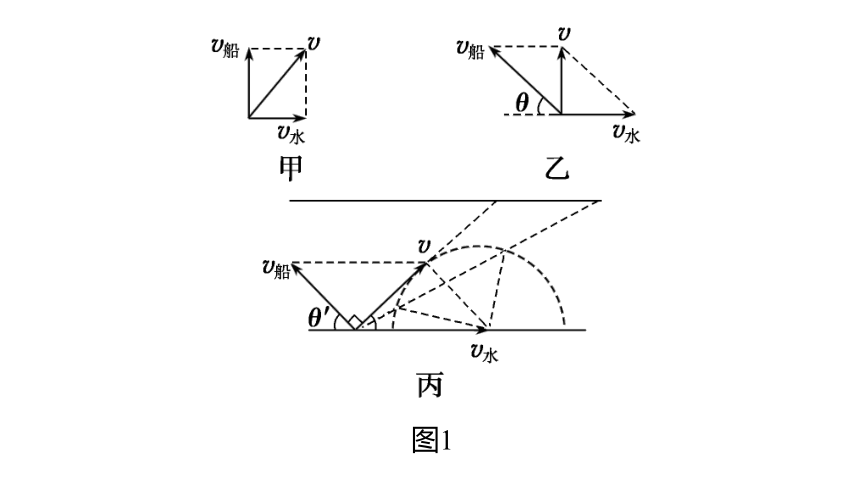
1.小船渡河运动分解
小船渡河时,实际参与了两个方向的分运动,即随水流的运动(水冲船的运动)和船在静水中的运动,船的实际运动是这两个分运动的合运动.
设河宽为d、水流的速度为v水(方向:沿河岸指向下游)、船在静水中的速度为v船(方向:船头指向)
图1
(1)最短时间
(2)最短航程
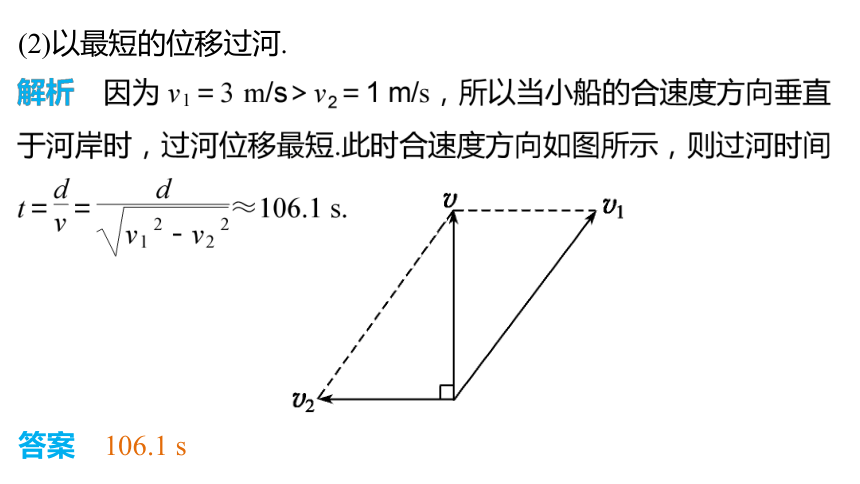
例1 有一只小船正在过河,河宽d=300 m,小船在静水中的速度v1=3 m/s,水的流速v2=1 m/s.小船以下列条件过河时,求过河的时间.
(1)以最短的时间过河.
答案 100 s
(2)以最短的位移过河.
答案 106.1 s
2.关联物体速度的分解
绳、杆等有长度的物体在运动过程中,其两端点的速度通常是不一样的,但两端点的速度是有联系的,我们称之为“关联”速度,解决“关联”速度问题的关键有两点:一是物体的实际运动是合运动,分速度的方向要按实际运动效果确定;二是沿杆(或绳)方向的分速度大小相等.
例2 如图2所示,汽车甲以速度v1拉汽车乙前进,乙的速度为v2,甲、乙都在水平面上运动,求此时两车的速度之比v1∶v2.
解析 甲、乙沿绳的速度分别为v1和v2cos α,两者应该相等,所以有v1=v2cos α,
故v1∶v2=cos α∶1
答案 cos α∶1
图2
二、解决平抛运动问题的三个突破口
1.把平抛运动的时间作为突破口
平抛运动规律中,各物理量都与时间有联系,所以只要求出抛出时间,其他的物理量都可轻松解出.
2.把平抛运动的偏转角作为突破口
图3
3.把平抛运动的一段轨迹作为突破口
平抛运动的轨迹是一条抛物线,已知抛物线上的任意一段,就可求出水平初速度和抛出点,其他物理量也就迎刃而解了.设图4为某小球做平抛运动的一段轨迹,在轨迹上任取两点A和B,E为AB的中间时刻.(如图所示)
图4
设tAE=tEB=T
由竖直方向上的匀变速直线运动得FC-AF=gT2,所以
由水平方向上的匀速直线运动得
例3 如图5所示,在倾角为37°的斜面上从A点以6 m/s的初速度水平抛出一个小球,小球落在B点,求小球刚碰到斜面时的速度方向与水平方向夹角的正切值及A、B两点间的距离和小球在空中飞行的时间.(g取10 m/s2)
图5
解析 如图所示,设小球落到B点时速度的偏转角为α,运动时间为t.
解得t=0.9 s
由x=v0t=5.4 m
三、分析圆周运动问题的基本方法
1.分析物体的运动情况,明确圆周轨道在怎样的一个平面内,确定圆心在何处,半径是多大.
2.分析物体的受力情况,弄清向心力的来源跟运用牛顿第二定律解直线运动问题一样,解圆周运动问题,也要先选择研究对象,然后进行受力分析,画出受力示意图.
例4 如图6所示,两根长度相同的轻绳(图中未画出),连接着相同的两个小球,让它们穿过光滑的杆在水平面内做匀速圆周运动,其中O为圆心,两段细绳在同一直线上,此时,两段绳子受到的拉力之比为多少?
图6
解析 设每段绳子长为l,对球2有F2=2mlω2
对球1有:F1-F2=mlω2
由以上两式得:F1=3mlω2
答案 3∶2
四、圆周运动中的临界问题
1.临界状态:当物体从某种特性变化为另一种特性时发生质的飞跃的转折状态,通常叫做临界状态,出现临界状态时,既可理解为“恰好出现”,也可理解为“恰好不出现”.
3.轻杆类:
(1)小球能过最高点的临界条件:v=0.
图7
图8
例5 如图9所示,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动.现测得转台半径R=0.5 m,离水平地面的高度H=0.8 m,物块平抛落地过程水平位移的大小x=0.4 m.设物块所受的最大静摩擦力等于滑动摩擦力,取重力加速度g=10 m/s2.求:
图9
(1)物块做平抛运动的初速度大小v0;
在水平方向上有x=v0t②
代入数据得v0=1 m/s
答案 1 m/s
(2)物块与转台间的动摩擦因数μ.
Ffm=μFN=μmg④
代入数据得μ=0.2
答案 0.2
例6 如图10所示,AB为半径为R的金属导轨(导轨厚度不计),a、b为分别沿导轨上、下两表面做圆周运动的小球(可看作质点),要使小球不致脱离导轨,则a、b在导轨最高点的速度va、vb应满足什么条件?
图10
解析 对a球在最高点,由牛顿第二定律得:
要使a球不脱离轨道,
则FNa>0②
对b球在最高点,由牛顿第二定律得:
要使b球不脱离轨道,
则FNb>0④
1.(运动的合成和分解)某河宽为600 m,河中某点的水流速度v与该点到较近河岸的距离d的关系如图11所示.船在静水中的速度为4 m/s,要想使船渡河的时间最短,下列说法正确的是( )
自我检测
图11
1
2
3
1
2
3
A.船在航行过程中,船头应与河岸垂直
B.船在河水中航行的轨迹是一条直线
C.渡河的最短时间为240 s
解析 若船渡河的时间最短,船在航行过程中,必须保证船头始终与河岸垂直,选项A正确;
因水流的速度大小发生变化,根据运动的合成与分解可知,船在河水中航行的轨迹是一条曲线,选项B错误;
1
2
3
则船离开河岸400 m时的速度大小为
答案 AD
2.(平抛运动分析)如图12所示,P是水平面上的圆弧凹槽.从高台边B点以某速度v0水平飞出的小球,恰能从固定在某位置的凹槽的圆弧轨道的左端A点沿圆弧切线方向进入轨道.O是圆弧的圆心,θ1是OA与竖直方向的夹角,θ2是BA与竖直方向的夹角.则( )
图12
1
2
3
1
2
3
所以tan θ1·tan θ2=2,故B正确.
答案 B
3.(圆周运动中的临界问题)如图13所示,细绳的一端系着质量为M=2 kg的物体,静止在水平圆盘上,另一端通过光滑的小孔吊着质量为m=0.5 kg的物体,M的中点与圆孔的距离为0.5 m,并已知M与圆盘的最大静摩擦力为4 N,现使此圆盘绕中心轴线转动,求角速度ω在什么范围内可使m处于静止状态.(g取10 m/s2)
1
2
3
图13
1
2
3
代入数据得:ω1=1 rad/s.
当ω取较大值ω2时,M有背离O点滑动趋势,
此时M所受静摩擦力指向圆心O,
解析 当ω取较小值ω1时,M有向O点滑动趋势,此时M所受静摩擦力背离圆心O,对M有:
1
2
3
代入数据得:ω2=3 rad/s
所以角速度的取值范围是:1 rad/s≤ω≤3 rad/s.
答案 1 rad/s≤ω≤3 rad/s
第五章
曲线运动
专题整合
自我检测
学案9 章末总结
网络构建
网络构建
切线
物体所受合力的方向与
它的速度方向不在同一直线上
平行四边形定则
曲线运动
匀速直线
自由落体
匀变速曲线
曲线运动
曲线运动实例
圆周运动
竖直平面内的圆周运动
最高点速度恰好为零
0
一、运动的合成和分解
专题整合
1.小船渡河运动分解
小船渡河时,实际参与了两个方向的分运动,即随水流的运动(水冲船的运动)和船在静水中的运动,船的实际运动是这两个分运动的合运动.
设河宽为d、水流的速度为v水(方向:沿河岸指向下游)、船在静水中的速度为v船(方向:船头指向)
图1
(1)最短时间
(2)最短航程
例1 有一只小船正在过河,河宽d=300 m,小船在静水中的速度v1=3 m/s,水的流速v2=1 m/s.小船以下列条件过河时,求过河的时间.
(1)以最短的时间过河.
答案 100 s
(2)以最短的位移过河.
答案 106.1 s
2.关联物体速度的分解
绳、杆等有长度的物体在运动过程中,其两端点的速度通常是不一样的,但两端点的速度是有联系的,我们称之为“关联”速度,解决“关联”速度问题的关键有两点:一是物体的实际运动是合运动,分速度的方向要按实际运动效果确定;二是沿杆(或绳)方向的分速度大小相等.
例2 如图2所示,汽车甲以速度v1拉汽车乙前进,乙的速度为v2,甲、乙都在水平面上运动,求此时两车的速度之比v1∶v2.
解析 甲、乙沿绳的速度分别为v1和v2cos α,两者应该相等,所以有v1=v2cos α,
故v1∶v2=cos α∶1
答案 cos α∶1
图2
二、解决平抛运动问题的三个突破口
1.把平抛运动的时间作为突破口
平抛运动规律中,各物理量都与时间有联系,所以只要求出抛出时间,其他的物理量都可轻松解出.
2.把平抛运动的偏转角作为突破口
图3
3.把平抛运动的一段轨迹作为突破口
平抛运动的轨迹是一条抛物线,已知抛物线上的任意一段,就可求出水平初速度和抛出点,其他物理量也就迎刃而解了.设图4为某小球做平抛运动的一段轨迹,在轨迹上任取两点A和B,E为AB的中间时刻.(如图所示)
图4
设tAE=tEB=T
由竖直方向上的匀变速直线运动得FC-AF=gT2,所以
由水平方向上的匀速直线运动得
例3 如图5所示,在倾角为37°的斜面上从A点以6 m/s的初速度水平抛出一个小球,小球落在B点,求小球刚碰到斜面时的速度方向与水平方向夹角的正切值及A、B两点间的距离和小球在空中飞行的时间.(g取10 m/s2)
图5
解析 如图所示,设小球落到B点时速度的偏转角为α,运动时间为t.
解得t=0.9 s
由x=v0t=5.4 m
三、分析圆周运动问题的基本方法
1.分析物体的运动情况,明确圆周轨道在怎样的一个平面内,确定圆心在何处,半径是多大.
2.分析物体的受力情况,弄清向心力的来源跟运用牛顿第二定律解直线运动问题一样,解圆周运动问题,也要先选择研究对象,然后进行受力分析,画出受力示意图.
例4 如图6所示,两根长度相同的轻绳(图中未画出),连接着相同的两个小球,让它们穿过光滑的杆在水平面内做匀速圆周运动,其中O为圆心,两段细绳在同一直线上,此时,两段绳子受到的拉力之比为多少?
图6
解析 设每段绳子长为l,对球2有F2=2mlω2
对球1有:F1-F2=mlω2
由以上两式得:F1=3mlω2
答案 3∶2
四、圆周运动中的临界问题
1.临界状态:当物体从某种特性变化为另一种特性时发生质的飞跃的转折状态,通常叫做临界状态,出现临界状态时,既可理解为“恰好出现”,也可理解为“恰好不出现”.
3.轻杆类:
(1)小球能过最高点的临界条件:v=0.
图7
图8
例5 如图9所示,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动.现测得转台半径R=0.5 m,离水平地面的高度H=0.8 m,物块平抛落地过程水平位移的大小x=0.4 m.设物块所受的最大静摩擦力等于滑动摩擦力,取重力加速度g=10 m/s2.求:
图9
(1)物块做平抛运动的初速度大小v0;
在水平方向上有x=v0t②
代入数据得v0=1 m/s
答案 1 m/s
(2)物块与转台间的动摩擦因数μ.
Ffm=μFN=μmg④
代入数据得μ=0.2
答案 0.2
例6 如图10所示,AB为半径为R的金属导轨(导轨厚度不计),a、b为分别沿导轨上、下两表面做圆周运动的小球(可看作质点),要使小球不致脱离导轨,则a、b在导轨最高点的速度va、vb应满足什么条件?
图10
解析 对a球在最高点,由牛顿第二定律得:
要使a球不脱离轨道,
则FNa>0②
对b球在最高点,由牛顿第二定律得:
要使b球不脱离轨道,
则FNb>0④
1.(运动的合成和分解)某河宽为600 m,河中某点的水流速度v与该点到较近河岸的距离d的关系如图11所示.船在静水中的速度为4 m/s,要想使船渡河的时间最短,下列说法正确的是( )
自我检测
图11
1
2
3
1
2
3
A.船在航行过程中,船头应与河岸垂直
B.船在河水中航行的轨迹是一条直线
C.渡河的最短时间为240 s
解析 若船渡河的时间最短,船在航行过程中,必须保证船头始终与河岸垂直,选项A正确;
因水流的速度大小发生变化,根据运动的合成与分解可知,船在河水中航行的轨迹是一条曲线,选项B错误;
1
2
3
则船离开河岸400 m时的速度大小为
答案 AD
2.(平抛运动分析)如图12所示,P是水平面上的圆弧凹槽.从高台边B点以某速度v0水平飞出的小球,恰能从固定在某位置的凹槽的圆弧轨道的左端A点沿圆弧切线方向进入轨道.O是圆弧的圆心,θ1是OA与竖直方向的夹角,θ2是BA与竖直方向的夹角.则( )
图12
1
2
3
1
2
3
所以tan θ1·tan θ2=2,故B正确.
答案 B
3.(圆周运动中的临界问题)如图13所示,细绳的一端系着质量为M=2 kg的物体,静止在水平圆盘上,另一端通过光滑的小孔吊着质量为m=0.5 kg的物体,M的中点与圆孔的距离为0.5 m,并已知M与圆盘的最大静摩擦力为4 N,现使此圆盘绕中心轴线转动,求角速度ω在什么范围内可使m处于静止状态.(g取10 m/s2)
1
2
3
图13
1
2
3
代入数据得:ω1=1 rad/s.
当ω取较大值ω2时,M有背离O点滑动趋势,
此时M所受静摩擦力指向圆心O,
解析 当ω取较小值ω1时,M有向O点滑动趋势,此时M所受静摩擦力背离圆心O,对M有:
1
2
3
代入数据得:ω2=3 rad/s
所以角速度的取值范围是:1 rad/s≤ω≤3 rad/s.
答案 1 rad/s≤ω≤3 rad/s
