冀教版数学八年级上册 第十三章全等三角形达标测试卷(含答案)
文档属性
| 名称 | 冀教版数学八年级上册 第十三章全等三角形达标测试卷(含答案) | 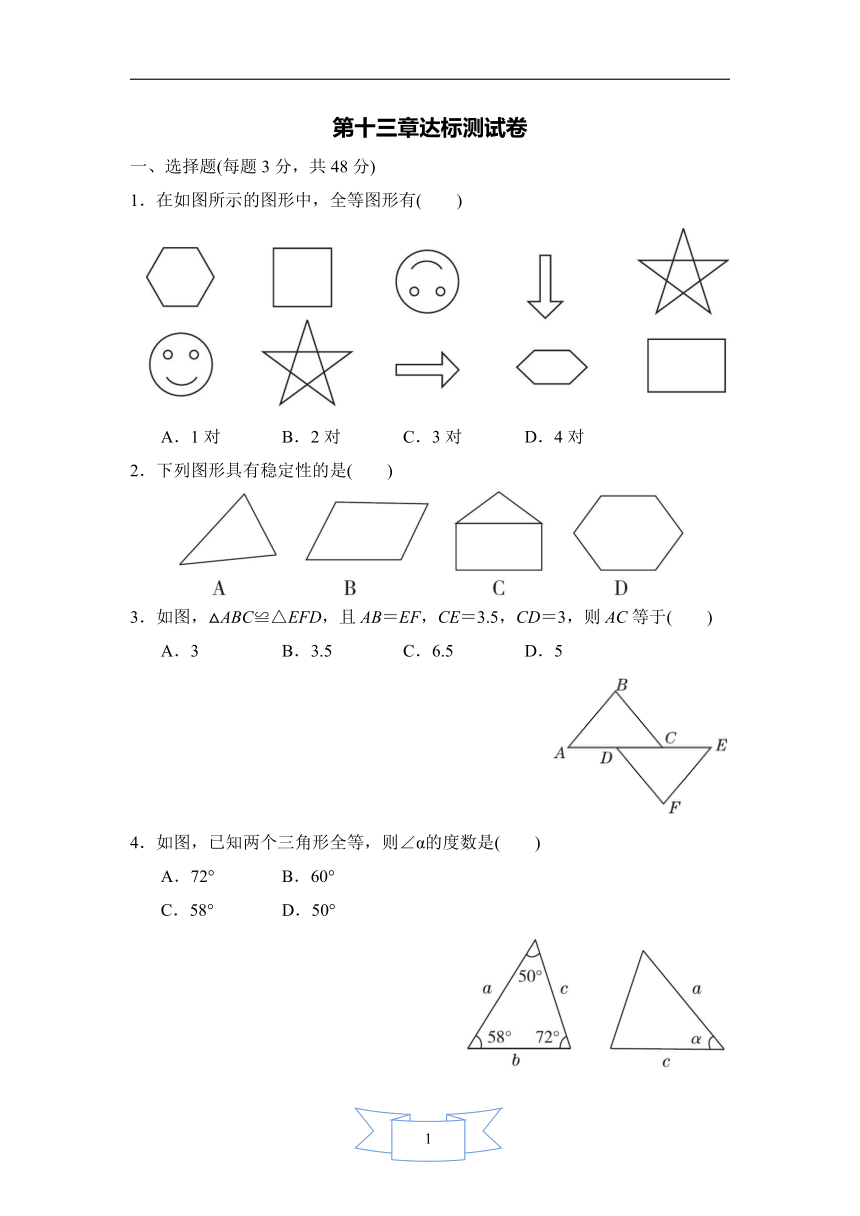 | |
| 格式 | zip | ||
| 文件大小 | 311.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-07 21:16:21 | ||
图片预览





文档简介
第十三章达标测试卷
一、选择题(每题3分,共48分)
1.在如图所示的图形中,全等图形有( )
A.1对 B.2对 C.3对 D.4对
2.下列图形具有稳定性的是( )
3.如图,△ABC≌△EFD,且AB=EF,CE=3.5,CD=3,则AC等于( )
A.3 B.3.5 C.6.5 D.5
4.如图,已知两个三角形全等,则∠α的度数是( )
A.72° B.60°
C.58° D.50°
5.对于下列各组条件,不能判定△ABC≌△A′B′C′的一组是( )
A.∠A=∠A′,∠B=∠B′,AB=A′B′ B.∠A=∠A′,AB=A′B′,AC=A′C′
C.∠A=∠A′,AB=A′B′,BC=B′C′ D.AB=A′B′,AC=A′C′,BC=B′C′
6.下列定理中,没有逆定理的是( )
A.同旁内角互补,两直线平行 B.直角三角形的两锐角互余
C.互为相反数的两个数的绝对值相等 D.同位角相等,两直线平行
7.如图,如果△ABC≌△FED,那么下列结论错误的是( )
A.EC=BD B.EF∥AB C.DF=BD D.AC∥FD
8.如图,B,D分别是位于线段AC两侧的点,连接AB,AD,CB,CD,则下列条件中,与AB=AD相结合无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC
C.∠BCA=∠DCA D.以上都无法判定
9.如图,在四边形ABCD中,CB=CD,∠B=90°,∠ACD=∠ACB,∠BAD=70°,则∠BCD的度数为( )
A.145° B.130° C.110° D.70°
10.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1,2,3,4的四块),聪明的小明经过仔细考虑认为只要带其中的两块碎片去玻璃店就可以让师傅配一块与以前一样的玻璃样板.你认为下列四个选项中考虑最全面的是( )
A.带其中的任意两块去都可以 B.带1,2或2,3去就可以了
C.带1,4或3,4去就可以了 D.带1,4或2,4或3,4去均可
11.如图,已知∠1=∠2,要使△ABC≌△ADE,还需条件( )
A.AB=AD,BC=DE B.BC=DE,AC=AE
C.∠B=∠D,∠C=∠E D.AC=AE,AB=AD
12.如图,是一个4×4的正方形网格,∠1+∠2+∠3+∠4+∠5+∠6+∠7等于( )
A.585° B.540° C.270° D.315°
13.如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE与CD相交于O,∠1=∠2,则图中的全等三角形有( )
A.1对 B.2对 C.3对 D.4对
14.根据下列条件利用尺规作图作△ABC,作出的△ABC不唯一的是( )
A.AB=7,AC=5,∠A=60° B.AC=5,∠A=60°∠C=80°
C.AB=7,AC=5,∠B=40° D.AB=7,BC=6,AC=5
15.如图,已知∠1=∠2,AC=AD,添加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有( )
A.4个 B.3个
C.2个 D.1个
16.如图,已知线段AB=18米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P从B向A运动,每秒走1米,Q从B向D运动,每秒走2米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
A.4 B.6 C.4或9 D.6或9
二、填空题(每题3分,共9分)
17.如果两个三角形的两边及其中一边的对角对应相等,那么这两个三角形全等,其逆命题是________________________________________,这个逆命题是________命题.
18.如图,△ABC的周长为32,AD⊥BC于点D,D是BC的中点,若△ACD的周长为24,那么AD的长为________.
19.如图,CA⊥BE,且△ABC≌△ADE,则BC与DE的关系是____________.
三、解答题(20题6分,26题12分,其余每题9分,共63分)
20.如图,已知∠1=∠2,∠3=∠4,EC=AD.求证:AB=BE.
21.如图,为了测量一幢楼的高AB,在旗杆CD与楼之间选定一点P.测得∠DPC+∠APB=90°,量得P到楼底的距离PB与旗杆的高度相等,等于8米,量得旗杆与楼之间的距离DB=33米,求楼高AB是多少米.
22.如图,已知等边三角形ABC,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.求∠DFC的度数.
23.如图,点D为码头,A,B两个灯塔与码头的距离相等,DA,DB为海岸线,一轮船离开码头,计划沿∠ADB的平分线航行,在航行途中的C点处,测得轮船与灯塔A和灯塔B的距离相等.试问:轮船航行是否偏离指定航线?请说明理由.
24.如图,已知直角α,线段m,利用尺规作直角三角形ABC,使∠C=90°,AC=m,BC=2m.不写作法,但要保留作图痕迹.
25.如图,已知正方形ABCD,从顶点A引两条射线分别交BC,CD于点E,F,且∠EAF=45°.求证:BE+DF=EF.
26.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)BF⊥CE,交CE于点F,交CD于点G(如图①),求证:AE=CG;
(2)AH⊥CE,交CE的延长线于点H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.
答案
一、1.C 点拨:本题是一道易错题,误认为图形的全等与图形的位置、方向等有关.
2.A 3.C 4.D 5.C 6.C 7.C
8.C 点拨:已知AB=AD,并且已知公共边AC,这两个条件与∠BCA=∠DCA相结合,不符合全等的条件,所以选C.
9.C 点拨:由“SAS”可得△ACD≌△ACB,所以∠BAC=∠DAC=35°,所以∠BCA=∠DCA=55°,则∠BCD=∠BCA+∠DCA=55°+55°=110°.
10.D 11.D 12.A 13.D
14.C 点拨:由于“两边和其中一边的对角对应相等的两个三角形不一定全等”,所以所作的三角形不唯一.
15.B 点拨:由∠1=∠2可得∠BAC=∠EAD,则已知三角形的一个角及其邻边对应相等.若按SAS判定可增加①;按ASA判定可增加③;按AAS判定可增加④,所以选B.
16.B
二、17.如果两个三角形全等,那么这两个三角形的两边及其中一边的对角对应相等;真
18.8 点拨:根据“AD⊥BC于点D,D是BC的中点”可由SAS证得△ABD≌△ACD,则△ABC的周长=△ACD的周长的2倍-2AD,即32=24×2-2AD,解得AD=8.
19.相等且垂直 点拨:由△ABC≌△ADE可知BC=DE,∠C=∠E.如图,延长ED交BC于点F,因为∠B+∠C=90°,所以∠B+∠E=90°,在△BEF中,由三角形内角和定理可求得∠BFE=90°,即BC⊥DE.
三、20.证明:∵∠1=∠2,
∴∠1+∠EBD=∠EBD+∠2,
即∠ABD=∠EBC.
在△ABD和△EBC中,
∴△ABD≌△EBC(AAS).
∴AB=BE.
21.解:由题意知∠CDP=∠ABP=90°.∵∠DPC+∠APB=90°,∠DPC+∠DCP=90°,
∴∠DCP=∠APB,
在△CPD和△PAB中,
∴△CPD≌△PAB(ASA),
∴PD=AB,∵DB=33米,PB=8米,
∴AB=PD=DB-PB=33-8=25(米).
答:楼高AB是25米.
22.解:∵△ABC为等边三角形,
∴AC=AB,∠B=∠BAC=∠ACB=60°.
在△AEC和△BDA中,
∵
∴△AEC≌△BDA(SAS).
∴∠ACE=∠BAD.
∴∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=∠BAC=60°.
23.解:轮船航行没有偏离指定航线.
理由如下:由题意知DA=DB,AC=BC.
在△ADC和△BDC中,
∴△ADC≌△BDC(SSS).
∴∠ADC=∠BDC,即DC为∠ADB的平分线.∴轮船航行没有偏离指定航线.
24.解:作出的△ABC如图所示.
25.证明:延长CD到点G,使DG=BE,连接AG.在正方形ABCD中,
AB=AD,∠B=∠ADC=90°,
∴∠ADG=∠B.
在△ABE和△ADG中,
∴△ABE≌△ADG(SAS).
∴AE=AG,∠BAE=∠DAG.
∵∠EAF=45°,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=90°-45°=45°.∴∠EAF=∠GAF.
在△AEF和△AGF中,
∴△AEF≌△AGF(SAS).
∴EF=GF.
∵GF=DG+DF=BE+DF,
∴BE+DF=EF.
26.(1)证明:∵点D是AB中点,
∴AD=BD.
又∵AC=BC,CD=CD,
∴△ACD≌△BCD(SSS).
∴∠ADC=∠BDC=90°,∠ACD=∠BCD=45°.
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG.
又∵BF⊥CE,
∴∠CBG+∠BCF=90°.
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG.
又∵AC=BC,
∴△AEC≌△CGB(ASA),
∴AE=CG.
(2)解:BE=CM.
证明:∵CH⊥HM,易得CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°.
∴∠CMA=∠BEC.
又∵AC=BC,∠ACM=∠CBE=45°,∴△CAM≌△BCE(AAS).
∴BE=CM.
一、选择题(每题3分,共48分)
1.在如图所示的图形中,全等图形有( )
A.1对 B.2对 C.3对 D.4对
2.下列图形具有稳定性的是( )
3.如图,△ABC≌△EFD,且AB=EF,CE=3.5,CD=3,则AC等于( )
A.3 B.3.5 C.6.5 D.5
4.如图,已知两个三角形全等,则∠α的度数是( )
A.72° B.60°
C.58° D.50°
5.对于下列各组条件,不能判定△ABC≌△A′B′C′的一组是( )
A.∠A=∠A′,∠B=∠B′,AB=A′B′ B.∠A=∠A′,AB=A′B′,AC=A′C′
C.∠A=∠A′,AB=A′B′,BC=B′C′ D.AB=A′B′,AC=A′C′,BC=B′C′
6.下列定理中,没有逆定理的是( )
A.同旁内角互补,两直线平行 B.直角三角形的两锐角互余
C.互为相反数的两个数的绝对值相等 D.同位角相等,两直线平行
7.如图,如果△ABC≌△FED,那么下列结论错误的是( )
A.EC=BD B.EF∥AB C.DF=BD D.AC∥FD
8.如图,B,D分别是位于线段AC两侧的点,连接AB,AD,CB,CD,则下列条件中,与AB=AD相结合无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC
C.∠BCA=∠DCA D.以上都无法判定
9.如图,在四边形ABCD中,CB=CD,∠B=90°,∠ACD=∠ACB,∠BAD=70°,则∠BCD的度数为( )
A.145° B.130° C.110° D.70°
10.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1,2,3,4的四块),聪明的小明经过仔细考虑认为只要带其中的两块碎片去玻璃店就可以让师傅配一块与以前一样的玻璃样板.你认为下列四个选项中考虑最全面的是( )
A.带其中的任意两块去都可以 B.带1,2或2,3去就可以了
C.带1,4或3,4去就可以了 D.带1,4或2,4或3,4去均可
11.如图,已知∠1=∠2,要使△ABC≌△ADE,还需条件( )
A.AB=AD,BC=DE B.BC=DE,AC=AE
C.∠B=∠D,∠C=∠E D.AC=AE,AB=AD
12.如图,是一个4×4的正方形网格,∠1+∠2+∠3+∠4+∠5+∠6+∠7等于( )
A.585° B.540° C.270° D.315°
13.如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE与CD相交于O,∠1=∠2,则图中的全等三角形有( )
A.1对 B.2对 C.3对 D.4对
14.根据下列条件利用尺规作图作△ABC,作出的△ABC不唯一的是( )
A.AB=7,AC=5,∠A=60° B.AC=5,∠A=60°∠C=80°
C.AB=7,AC=5,∠B=40° D.AB=7,BC=6,AC=5
15.如图,已知∠1=∠2,AC=AD,添加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有( )
A.4个 B.3个
C.2个 D.1个
16.如图,已知线段AB=18米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P从B向A运动,每秒走1米,Q从B向D运动,每秒走2米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
A.4 B.6 C.4或9 D.6或9
二、填空题(每题3分,共9分)
17.如果两个三角形的两边及其中一边的对角对应相等,那么这两个三角形全等,其逆命题是________________________________________,这个逆命题是________命题.
18.如图,△ABC的周长为32,AD⊥BC于点D,D是BC的中点,若△ACD的周长为24,那么AD的长为________.
19.如图,CA⊥BE,且△ABC≌△ADE,则BC与DE的关系是____________.
三、解答题(20题6分,26题12分,其余每题9分,共63分)
20.如图,已知∠1=∠2,∠3=∠4,EC=AD.求证:AB=BE.
21.如图,为了测量一幢楼的高AB,在旗杆CD与楼之间选定一点P.测得∠DPC+∠APB=90°,量得P到楼底的距离PB与旗杆的高度相等,等于8米,量得旗杆与楼之间的距离DB=33米,求楼高AB是多少米.
22.如图,已知等边三角形ABC,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.求∠DFC的度数.
23.如图,点D为码头,A,B两个灯塔与码头的距离相等,DA,DB为海岸线,一轮船离开码头,计划沿∠ADB的平分线航行,在航行途中的C点处,测得轮船与灯塔A和灯塔B的距离相等.试问:轮船航行是否偏离指定航线?请说明理由.
24.如图,已知直角α,线段m,利用尺规作直角三角形ABC,使∠C=90°,AC=m,BC=2m.不写作法,但要保留作图痕迹.
25.如图,已知正方形ABCD,从顶点A引两条射线分别交BC,CD于点E,F,且∠EAF=45°.求证:BE+DF=EF.
26.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)BF⊥CE,交CE于点F,交CD于点G(如图①),求证:AE=CG;
(2)AH⊥CE,交CE的延长线于点H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.
答案
一、1.C 点拨:本题是一道易错题,误认为图形的全等与图形的位置、方向等有关.
2.A 3.C 4.D 5.C 6.C 7.C
8.C 点拨:已知AB=AD,并且已知公共边AC,这两个条件与∠BCA=∠DCA相结合,不符合全等的条件,所以选C.
9.C 点拨:由“SAS”可得△ACD≌△ACB,所以∠BAC=∠DAC=35°,所以∠BCA=∠DCA=55°,则∠BCD=∠BCA+∠DCA=55°+55°=110°.
10.D 11.D 12.A 13.D
14.C 点拨:由于“两边和其中一边的对角对应相等的两个三角形不一定全等”,所以所作的三角形不唯一.
15.B 点拨:由∠1=∠2可得∠BAC=∠EAD,则已知三角形的一个角及其邻边对应相等.若按SAS判定可增加①;按ASA判定可增加③;按AAS判定可增加④,所以选B.
16.B
二、17.如果两个三角形全等,那么这两个三角形的两边及其中一边的对角对应相等;真
18.8 点拨:根据“AD⊥BC于点D,D是BC的中点”可由SAS证得△ABD≌△ACD,则△ABC的周长=△ACD的周长的2倍-2AD,即32=24×2-2AD,解得AD=8.
19.相等且垂直 点拨:由△ABC≌△ADE可知BC=DE,∠C=∠E.如图,延长ED交BC于点F,因为∠B+∠C=90°,所以∠B+∠E=90°,在△BEF中,由三角形内角和定理可求得∠BFE=90°,即BC⊥DE.
三、20.证明:∵∠1=∠2,
∴∠1+∠EBD=∠EBD+∠2,
即∠ABD=∠EBC.
在△ABD和△EBC中,
∴△ABD≌△EBC(AAS).
∴AB=BE.
21.解:由题意知∠CDP=∠ABP=90°.∵∠DPC+∠APB=90°,∠DPC+∠DCP=90°,
∴∠DCP=∠APB,
在△CPD和△PAB中,
∴△CPD≌△PAB(ASA),
∴PD=AB,∵DB=33米,PB=8米,
∴AB=PD=DB-PB=33-8=25(米).
答:楼高AB是25米.
22.解:∵△ABC为等边三角形,
∴AC=AB,∠B=∠BAC=∠ACB=60°.
在△AEC和△BDA中,
∵
∴△AEC≌△BDA(SAS).
∴∠ACE=∠BAD.
∴∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=∠BAC=60°.
23.解:轮船航行没有偏离指定航线.
理由如下:由题意知DA=DB,AC=BC.
在△ADC和△BDC中,
∴△ADC≌△BDC(SSS).
∴∠ADC=∠BDC,即DC为∠ADB的平分线.∴轮船航行没有偏离指定航线.
24.解:作出的△ABC如图所示.
25.证明:延长CD到点G,使DG=BE,连接AG.在正方形ABCD中,
AB=AD,∠B=∠ADC=90°,
∴∠ADG=∠B.
在△ABE和△ADG中,
∴△ABE≌△ADG(SAS).
∴AE=AG,∠BAE=∠DAG.
∵∠EAF=45°,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=90°-45°=45°.∴∠EAF=∠GAF.
在△AEF和△AGF中,
∴△AEF≌△AGF(SAS).
∴EF=GF.
∵GF=DG+DF=BE+DF,
∴BE+DF=EF.
26.(1)证明:∵点D是AB中点,
∴AD=BD.
又∵AC=BC,CD=CD,
∴△ACD≌△BCD(SSS).
∴∠ADC=∠BDC=90°,∠ACD=∠BCD=45°.
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG.
又∵BF⊥CE,
∴∠CBG+∠BCF=90°.
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG.
又∵AC=BC,
∴△AEC≌△CGB(ASA),
∴AE=CG.
(2)解:BE=CM.
证明:∵CH⊥HM,易得CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°.
∴∠CMA=∠BEC.
又∵AC=BC,∠ACM=∠CBE=45°,∴△CAM≌△BCE(AAS).
∴BE=CM.
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
